1. Физические свойства и параметры жидкостей. Основные элементы потоков и виды течений. Кавитация.
Жидкостью называют физическое тело, характеризующееся свойством текучести, обусловленное высокой степенью подвижности частиц жидкости друг относительно друга.
Различают капельные и газообразные жидкости.
Физические свойства жидкостей:
1)Плотностью жидкости называют массу единицы объема жидкости. Если объем жидкости Vимеет массу М, то плотность равна p=M/V.
Плотность жидкости зависит от температуры, давления и солености, однако в большинстве случаев влиянием температуры и давления на жидкость несжимаемых жидкостей можно пренебречь.
2)Весомость жидкости характеризуется ее сдельным весом (или объемным весом). Удельным весом y называют вес единицы объема жидкости. у=G/V (кН/м3)
3) Вязкостью жидкости называют свойство, в силу которого в ней проявляются силы внутреннего трения препятствующие сдвигающим усилиям. При малых скоростях движение жидкости вблизи поверхности тела имеет ламинарный (слоистый) характер. Отдельные слои жидкости движутся почти параллельными струйками без переноса конечных малых объемов жидкости из одного слоя в соседние.
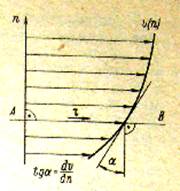
При движении слоев жидкости с различными скоростями между ними возникают напряжения внутреннего трения т, значения которых согласно закону Ньютона пропорциональны градиенту скорости ди/дп по нормали п к плоскости скольжения АВ : τ=µ(dv\dn)
При решении ряда теоретических вопросов в целях упрощения изучения явлений, связанных с обтеканием тел жидкостью, в (гидродинамике часто пользуются понятием идеальной жидкости. В отличие от реальной абстрактная идеальная жидкость абсолютно несжимаема и обладает абсолютной подвижностью т. е. лишена вязкости. Коэффициенты μ и v идеальной жидкости равны нулю. Однако все выводы, сделанные для идеальной жидкости, корректируются или дополняются применительно к реальной жидкости.
При обтекании жидкостью твердых тел свойство вязкости проявляется наиболее полно лишь в зоне, непосредственно примыкающей к телу, называемой пограничным слоем.
В пределах пограничного слоя скорости частиц жидкости изменяются от нуля на поверхности тела до значения скорости внешней среды на границе слоя.
Виды течения жидкостей.
В гидромеханике рассматривают два основных режима течения жидкости - ламинарный и турбулентный. При ламинарном движении связь между движущимися слоями осуществляется силами молекулярного сцепления частиц. Т. о., ламинарное движение жидкости характеризуется струйным течением, при котором отдельные ее слои движутся с различными скоростями в плоскостях, приблизительно параллельных поверхности границы потока. Сдвиг слоев сопровождается образованием касательных напряжений трения, подчиняющихся закону Ньютона.
При турбулентном движении частицы жидкости помимо главного направления перемещаются в поперечном направлении. Следовательно, при турбулентном движении перенос количества движения из одного слоя в другой осуществляется главным образом путем перехода отдельных объемов жидкости из слоя в слой.
Линия тока- это линия, касательная к векторам скорости каждой из рассматриваемых частиц, полученная в конкретный момент времени.
Трубка тока(элементарная струйка) – часть потока однородной жидкости, проходящая через бесконечно малую площадку с одинаковыми скоростями линий тока. Основным свойством трубки тока является невозможность выхода частиц жидкости за стенки трубки тока.
Кавитация. Из уравнения Бернулли следует, что с увеличением скорости должно падать давление. При достаточно больших скоростях потока давление в точках, где коэффициент давления имеет минимальное значение, может упасть до давления насыщенных паров pd при котором жидкость начнет кипеть. Это явление вскипания жидкости без ее нагрева называют в гидромеханике кавитацией. Появлению кавитации способствуют растворенные в воде воздух и газы, которые выделяются при понижении давления. Пары жидкости и выделившиеся из нее воздух и газы образуют полости, именуемые кавитационными кавернами.
Существует три вида кавитации: пузырчатая, пленочная и вихревая.
При пузырчатой кавитации каверны в виде отдельных пузырьков располагаются по телу разрозненными группами. По мере развития процесса отдельные пузырьки сливаются и образуют пленочную кавитацию, при которой каверны существуют в виде тонких длинных полос. В ядрах вихрей возникает вихревая кавитация. Из-за различного рода случайных причин кавитационная каверна и, в первую очередь, ее задняя кромка неустойчивы и пульсируют. Если при замыкании каверны на теле часть каверны в результате пульсаций попадает в область, где р > рd, то пар в этом месте конденсируется, что происходит практически мгновенно и сопровождается звуковым импульсом и гидравлическими ударами. Этот процесс называется захлопыванием (замыканием) пузырьков каверны. При замыкании каждого пузырька внутри него в течение миллисекунд и даже микросекунд возникают высокие давления. Вследствие малой площади сечения пузырьков и высоких давлений импульсного характера в материале тела возникают ^напряжения, во много раз превосходящие его предел текучести. Происходит выкол материала, появляются трещины, интенсифицируется процесс коррозии. Такое разрушение материала называют кавитационной эрозией.
Из сказанного следует, что кавитация на телах (крыльях, лопастях гребных винтов) нежелательна. Для отдаления момента начала кавитации следует по возможности увеличивать заглубление тела, поднимая тем самым давление на поверхности тела, либо уменьшать пики разрежения £. Для уменьшения £ следует придавать телу более обтекаемую форму, увеличивая его длину по сравнению с шириной (толщиной).
2. Уравнение Бернулли. Связь скорости и давления в потоке. Структура формулы для силы в гидродинамике.
Выражением закона сохранения энергии в гидромеханике является уравнение Бернулли, связывающее между собой давление, скорость и характеристики жидкости. Будем считать, что жидкость идеальна и несжимаема, ее движение носит установившийся характер, а из массовых сил действует только вес. Выделим в элементарной струйке объем жидкости, образованный сечениями 1 и 2 (рис. 4.6). В течение малого промежутка времени δt этот объем переместится в положение 1'-2', причем сечение 1 передвинется на расстояние δl1 = υ1δt а сечение 2 - на расстояние δl2 = υ2δt. Из уравнения неразрывности следует, что расход жидкости через любое сечение струйки должен быть одинаков, поэтому объем жидкости 1-1' должен быть равен объему 2-2'. Обозначив этот объем через б V, получим
δV = ω1δ11 = ω2δl2,
где ω1 и ω2 - площади сечений 1 и 2.
В результате получаем: z+ p/γ+ υ 2 /(2g) = const.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.