Это уравнение показывает, что сумма высоты положения сечения z пьезометрического запора p/γ и скоростного напора υ 2 /(2g) является постоянной величиной для всех сечений данной элементарной струйки. В гидромеханике используют также другую форму уравнения Бернулли:
γz + p + ρυ2/2 = const.
Первый член этого уравнения выражает удельную (отнесенную к единице веса) потенциальную энергию сил тяжести (энергию положения), второй - удельную потенциальную энергию давления и третий -удельную кинетическую энергию. Таким образом, удельная механическая энергия на всем пути движения жидкости в элементарной струйке остается постоянной, но при переходе к другой струйке ее значение может измениться.
При рассмотрении реальной жидкости в уравнении Бернулли вводят поправки на преодоление сил сопротивления, но физическая сущность уравнения и выражаемого им закона сохранения энергии и взаимозависимости скорости потока и давления в нем остается неизменной.
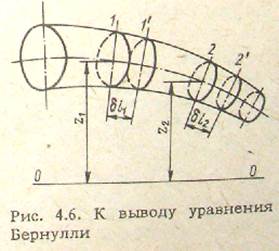
Коэффициент давления и его свойства. Рассмотрим обтекание симметричного профиля (например, ватерлинии судна, крыла или лопасти гребного винта) потоком безграничной жидкости, имеющим скорость υ0 . Остановимся на двух точках одной и той же линии тока, идущей из бесконечности по оси симметрии и разветвляющейся в носовой критической точке. Первая точка А находится далеко перед телом в невозмущенном потоке, где скорость равна υ0, давление р0 ; а вторая точка В - в произвольном месте на теле, где скорость о, давление р. Так как обе точки располагаются на одной линии тока, можно связать между собой скорости и давления в этих «точках с помощью уравнения Бернулли :
ρυ0 2/2 + p0 + γz0 = pυ2/2 + p + γz
Здесь z-Zq. Представив левую и правую части уравнения в безразмерном виде и разделив его на ρυ0 2/2, получим
(р- p0)/( ρυ0 2/2)=1-υ2/υ0 2.
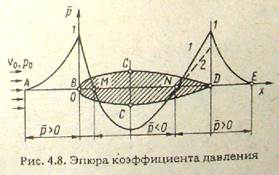
Левую часть этого выражения называют коэффициентом давления и обозначают р. Величина р-р0, находящаяся в числителе, характеризует избыточное давление (по сравнению с давлением в набегающем невозмущенном потоке). Величину ρυ0 2/2, стоящую в знаменателе, называют скоростным напором. Таким образом,
pˉ= (р- p0)/( ρυ0 2/2), или
p‾=1-(υ/ υ0) 2.
Использование р‾ для характеристики давления удобно потому, что его значение, во-первых, не зависит от рода жидкости и, во-вторых, не зависит от скорости набегающего потока, являясь лишь функцией формы тела, которая определяет соотношение υ/ υ0. Полученные выводы относятся, строго' говоря, к невязкой жидкости, однако они остаются практически верными и для движения хорошо обтекаемых тел в реальной вязкой жидкости.
Структура формулы для силы в гидродинамике:
R=ξ(ρV2/2)Ω
3. Геометрические и гидродинамические характеристики крыльев. Подводные крылья.
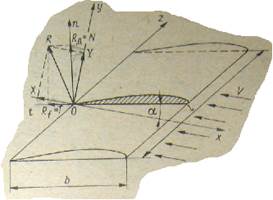
Для объяснения механизма возникновения подъемной силы рассмотрим крыло (рис. 4.9), ориентированное относительно поточной системы координат, в которой ось х совпадает с направлением скорости потока о, ось у перпендикулярна к ней и направлена вверх, а ось zнаправлена вдоль крыла. Протяженность крыла в направлении оси zназывают размахом крыла (удлинением) l. Если рассечь крыло плоскостью уОх, то в ее пересечении с крылом получится профиль крыла. В зависимости от требований к гидродинамическим характеристикам применяют сегментные, авиационные, клиновидные и другие профили.
Форма профиля крыла характеризуется следующими геометрическими параметрами:
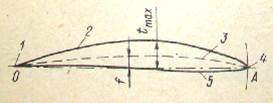
1 – задняя кромка; 2 – спинка; 3 – линия средней кривизны; 4 – носик; 5 – брюшко;
- относительной толщиной профиля, т. е. отношением его максимальной толщины к хорде (в процентах)
t=(tmax /b)100%, где хорда профиля b=ОА - радиус окружности, проведенной из его задней кромки О через крайнюю точку носика А;
- относительной кривизной профиля (в процентах)
χ=(f/b)• 100%, где/- максимальная ордината линии средней кривизны:
- средней геометрической хордой - отношением площади проекции крыла в плане Sк его размаху: bcp=S/l;
- относительным удлинением к, под которым понимают отношение размаха крыла к средней хорде:λ=l/bcp=l2/S.
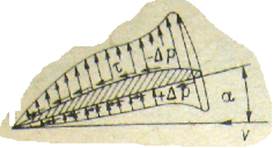
В соответствии с законом Бернулли на спинке профиля будет наблюдаться разрежение (-∆р), на брюшке - повышение давления (+∆р) Разность давлений обусловливает результирующую сил давлений Rд. Вязкость потока определяет наличие на профиле силы трения Rf . Результирующую этих сил Rназывают гидродинамической силой. Проекцию этой силы на ось х именуют силой лобового или профильного сопротивления X, проекция силы R на ось у - подъемной силой Y. При изучении сил, возникающих на руле как на крыле, используют систему координат, связанную с крылом. В этом случае проекция R на ось п определяет нормальную силу N = Rд , а проекция R на ось t - тангенциальную силу T= Rf.
Рассмотренные силы пропорциональны плотности жидкости ρ, площади крыла S и квадрату скорости υ2 и определяются следующими формулами гидромеханики:
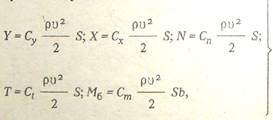
где Су, Сх - безразмерные коэффициенты подъемной силы и лобового сопротивления; Сn, Сt - безразмерные коэффициенты нормальной и касательной сил; Ст - безразмерный коэффициент момента. Коэффициенты Су, Сх, Сп, Сt Ст называют гидродинамическими характеристиками крыла. Они зависят в основном от формы профилей, а для крыла заданных размеров и формы профиля - от угла атаки.
4. Образование гидродинамической реакции на крыле в потоке. Подъемная сила и профильное сопротивление. Кризис обтекания. Угол атаки нулевой подъемной силы.
Угол между направлением скорости набегающего потока и хордой крыла называют углом атаки. При движении крыла в жидкости со скоростью υ под некоторым углом атаки α на верхней части профиля, называемой спинкой, будет наблюдаться сужение потока и, следовательно, увеличение скорости, а на нижней части - уменьшение скорости потока
В соответствии с законом Бернулли на спинке профиля будет наблюдаться разрежение (-∆р), на брюшке - повышение давления (+∆р) Разность давлений обусловливает результирующую сил давлений Rд. Вязкость потока определяет наличие на профиле силы трения Rf . Результирующую этих сил Rназывают гидродинамической силой.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.