Довольно полную картину о качке дают так называемые амплитудно-частотные характеристики (АЧХ) отдельных видов качки, под которыми понимают зависимость амплитуды какого-либо вида качки от частоты волнения. Очевидно, что эти зависимости, кроме всех прочих факторов, будут различными при изменении интенсивности волнения. Иногда АЧХ представляют в безразмерном виде, относя амплитуду качки к полувысоте волн, делая тем самым данную АЧХ универсальной для волнения любой интенсивности.
22. Качка судна на тихой воде. Собственные частоты и периоды.
Капитанские формулы.
Прежде чем строить уравнения качки судна на морском волнении, целесообразно рассмотреть виды качки судна на тихой воде. Несмотря на то, что качка на тихой воде (качка от порыва ветра, качка при работе судовыми грузовыми средствами) встречается на практике довольно редко, роль теории этой качки чрезвычайно важна. Исследуя качку судна на тихой воде (т. е. качку при отсутствии периодических возмущающих сил и моментов), удается определить важные колебательные свойства судна - так называемые характеристики собственных (или свободных) колебаний судна, необходимые при исследовании качки на волнении, собственные периоды и частоты качки всех трех видов, а также коэффициенты сопротивления корпуса судна.
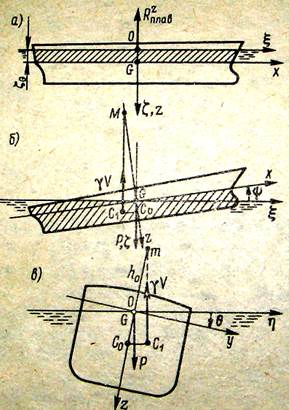
Силы и моменты сил, действующие на судно при качке на тихой воде: а - сила плавучести Rzплав; б - продольный восстанавливающий момент Myплав; в - Поперечный восстанавливающий момент Mxплав .
частота собственных колебаний n судна (без учета сопротивления) на тихой воде и коэффициенты демпфирования 2ν равны: для вертикальной качки:

для бортовой качки:
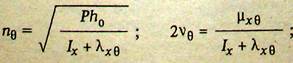
для килевой качки:
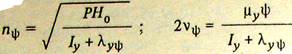
Широкое распространение имеют приближенные формулы 'для оценки собственных периодов различных видов качки на тихой воде, которые получаются в результате применения приближенных зависимостей для моментов инерции и присоединенных масс и подстановки их в выражения:
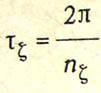
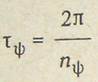
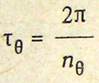
Формулу:
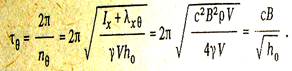
входящую в состав так называемых капитанских формул, применяют не только для оценки периода τθ по рассчитанной начальной метацентрической высоте h0, но и для экспериментальной проверки расчета остойчивости путем раскачивания судна и замера среднего периода собственных бортовых колебаний на тихой воде и последующего контроля h0:h0 = (сВ/τθ)2.
28. Перечень задач, решаемых на штормовых диаграммах.
Диаграммы для расчета гребных винтов позволяют решать многие эксплуатационные задачи, в том числе задачи, необходимые судоводителю. В частности, с помощью этих диаграмм определяют достижимую скорость судна, упор гребного винта, строят паспортные диаграммы.
Диаграммы для расчета гребных винтов являются результатом систематических испытаний моделей гребных винтов в опытовых бассейнах или специальных лабораториях - в кавитационных трубах. Эти испытания позволяют установить взаимосвязь всех геометрических характеристик (Нв /DB; θ; z; D0 /DBи др.) и их влияние на эффективность работы гребных винтов. Испытания моделей гребных винтов заключаются в измерении упора Р и момента Мр гребного винта при различных частотах вращения n и различной скорости поступательного движения υр. Результаты испытаний обрабатываются в виде кривых действия гребного винта . Серии моделей винтов обычно варьируются по HB/DB; θ; zпри сохранении контура лопастей, формы лопастных сечений, их относительной толщины к относительного диаметра ступицы. Кривые действия гребного винта позволяют решать проектные и эксплуатационные задачи, причем обычно достаточно располагать кривыми К1= f(λp) и ηр = f(λp) либо К2 = f(λp) и ηр = f(λp) в зависимости от того, какая задача решается.
В мировой практике для этих целей широко используют диаграммы, построенные на основе кривых действия гребных винтов. Оригинальная форма таких диаграмм, получившая признание в нашей стране, предложена Э. Э. Папмелем. Существо ее заключается в том, что на кривых действия серийных винтов соединяются точки с одинаковым значением КПД на линиях К1= f(λp) и К2= f(λp) .В результате получаются две диаграммы - одна для решения задач, когда выбирается двигатель, другая - обратная, когда его характеристики известны и для них с помощью диаграммы рассчитываются элементы винта и скорость судна. По обеим диаграммам легко определить оптимальные диаметр винта или частоту его. вращения, скорость судна или упор винта, его шаговое отношение, потребляемую мощность двигателя и т. д. Если диаметр или частота вращения не известны, то такую задачу можно решить методом последовательных приближений. Для облегчения решений задач с помощью диаграмм Папмелем был предложен ряд расчетных коэффициентов, позволяющих в зависимости от условия задания решать прикладные задачи по ходкости судна.
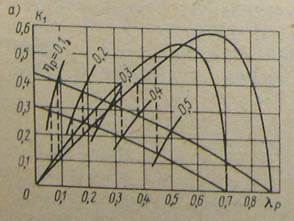
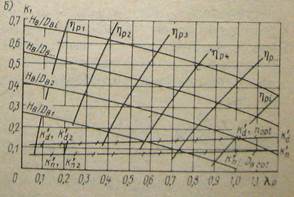
На рис. представлены схема построения диаграммы(a) и ее общий вид(b). Схема построена в координатах К1 - λp , очевидно, что вторая половина диаграммы - в координатах К1 - λp- будет аналогичной.
Перечень задач:
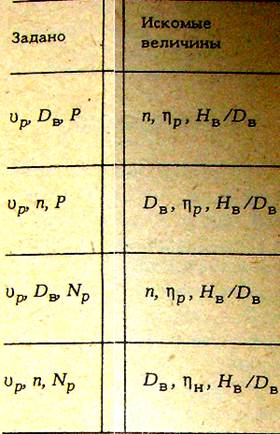
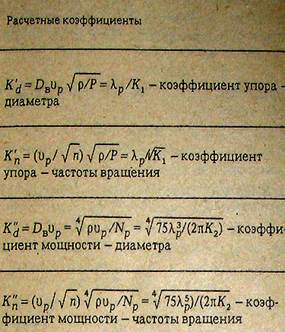
Для облегчения решений задач с помощью диаграмм Папмелем был предложен ряд расчетных коэффициентов, позволяющих в зависимости от условия задания решать прикладные задачи по ходкости судна. Упомянутые условия и расчетные коэффициенты, с помощью которых они решаются, сведены в табл. 6.1.
23. Амплитудно-частотная характеристика бортовой качки. Основной и параметрический резонанс . Влияние остойчивости па АЧХ.
Большее распространение получили АЧХ, представленные в безразмерном виде:
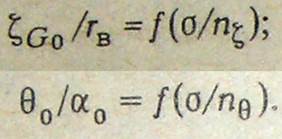
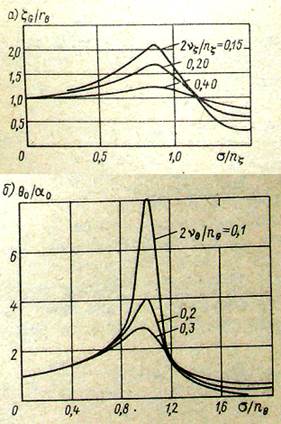
Амплитудно-частотные характеристики в безразмерном виде: а —вертикальной качки; б — бортовой качки
Из рис. 7.8 видно, что резонанс наблюдается при совпадении частот волнения и собственных колебаний. При σ>0 АЧХ стремятся к единице, т. е. при очень малых частотах волнения судно следит за волной. Его динамические свойства, в первую очередь инерция, проявляются при конечных частотах о, особенно в зоне резонанса. Характерно, что АЧХ вертикальной качки не имеет ярко выраженного резонансного пика.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.