Крутизна изменения частоты определяется девиацией частоты w и периодом модуляции Tм, который выбирается из условия tDmax<< Tм. Отраженный от цели сигнал имеет аналогичные параметры, только он смещен на величину tD (на рис. 26 это показано пунктирной линией). Частота первого гетеродина в приемнике имеет тот же закон частотной модуляции. На рис. 26 это показано штрихпунктирной линией. Следовательно, частота гетеродина за время распространения сигнала в режиме измерения не остается неизменной, как это было в режиме обнаружения. Благодаря этому отраженный от цели сигнал в режиме измерения на промежуточной частоте fпр. приобретает дополнительное частотное смещение, по сравнению с режимом обнаружения, и это смещение пропорционально однозначной дальности D.
Если частоту излученного сигнала представить
,
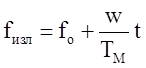тогда частота отраженного сигнала
.
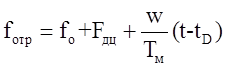Частота гетеродина приемника соответственно
.
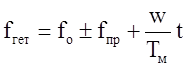Так как частота гетеродина может быть fгет>fo или
fгет<fo, то в выражение вводится ±fпр (рис. 26). Тогда разностная частота fраз пр1
с учетом промежуточной частоты fпр при
условии fгет>fo и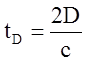 
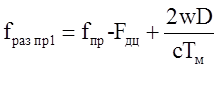, (23)
При условии fгет<fo имеем
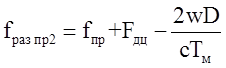. (24)
Частота Fдц определяется в режиме обнаружения по номеру фильтра, а fпр в этом режиме при fгет>fо имеет вид
,
при fгет<fo.
.
Следовательно, в режиме измерения
дальности обнаружение произойдет в другом фильтре, который отличается от начального
на величину изменения частоты ±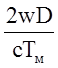 
[формулы (23),
(24)].
По разности частот между фильтрами в двух режимах измерения определяется однозначная дальность.
При анализе выражений (23) и (24) возникает вопрос выбора частоты гетеродина. На рис. 27 представлена зависимость величины промежуточной частоты fпр от дальности обнаружения D для двух значений частоты гетеродина.
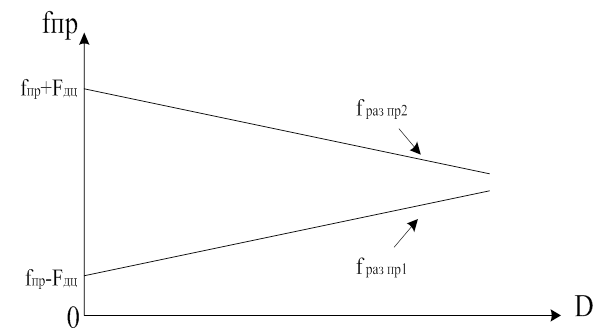
Рис. 27
При fгет>fo величина fраз пр1 увеличивается с увеличением дальности. Если fгет<fo, то fраз пр2 уменьшается при увеличении дальности. Следовательно, смещение номера обнаруживающего фильтра от первоначального увеличивается при fгет>fo и уменьшается при fгет<fo.
В режиме ВЧП обнаружение цели, движущейся с максимальной скоростью, происходит в доплеровских фильтрах, номер которых приближается к максимальному (рис. 6, 7). При определении дальности до этой цели, при условии fгет>fo в режиме измерения, номер обнаруживающего фильтра может превысить максимальный n, вследствие чего обнаружение цели не произойдет. Следовательно, при использовании частотной модуляции частоту гетеродина следует выбирать из условия fгет<fo.
В режиме СЧП неоднозначность измерения скорости цели может привести к неправильному результату измерения дальности за счет изменения положения Fдц из зоны неоднозначности в зону однозначности и, наоборот, при использовании частотной модуляции. Поэтому применять частотную модуляцию для измерения дальности в режиме СЧП следует ограниченно.
Временное стробирование для измерения однозначной дальности лучше использовать в режиме СЧП, имеющую большую скважность, чем в режиме ВЧП. Величина скважности определяет число временных каналов устройства обработки.
Сущность метода заключается в том, что при изменении Fп на небольшую величину меняется номер временного канала, в котором происходит обнаружение. Пояснение метода приведено на рис. 28.
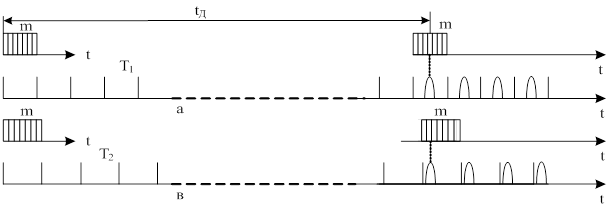
Рис. 28
T1 - период повторения при излучении импульсов с частотой Fп1, T2 - период повторения соответствующей Fп2, tD - время задержки, пропорциональное однозначной дальности. В импульсно-доплеровской РЛС tD>> T1 и T2, следовательно, отраженный от цели сигнал поступит в приемник через некоторое целое число периодов (x) частоты Fп1, как условно показано на рис. 28, а (такую последовательность нельзя увидеть). Отраженный сигнал, приходящий в x+1 периоде повторения T1, расположен в каком-то месте этого периода (рис. 28, а). При смене и соответствующем выборе периода повторения T2, причем T2 >T1, отраженный сигнал приходит в том же периоде x+1, но сместится влево (рис. 28, в) на величину Δt от места расположения в х+1 периоде повторения T1:
.
(25)
Если каким-то образом измерить величину Δt, то целое число периодов, предшествующих появлению сигнала, определяется как целая часть:
.
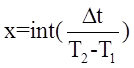(26)
Для измерения величины Δt применяются параллельные каналы устройства обработки со стробированием по дальности в пределах периода повторения T. Число стробируемых по дальности каналов равно m. На рис. 28 временные каналы условно показаны в двух периодах каждой частоты повторения.
Частоты повторения импульсов для определения однозначной дальности связаны между собой отношениями близко расположенных простых целых чисел m1, m2, m3.
Система с тремя частотами повторения импульсов, равными 10, 11, 12, дает однозначный отсчет дальности в 10*12=120 раз большей, чем система с одной частотой повторения (средней из указанных трех частот).
Желательно выбирать величину m1 в пределах 8-50. Это исходит из следующих соображений:
а) для упрощения аппаратуры число m1 должно быть малым, т.к. требуется максимальное число m=m1-1 параллельных каналов;
б) вероятность затенения цели за счет слепых дальностей, по крайней мере на одной частоте повторения импульсов, равна приблизительно 3/m1 (для РЛС с тремя частотами повторения), поэтому m1 должна ровняться 8 и более, так как дальность нельзя будет измерить, если цель затеняется на каждой частоте повторения;
в) для получения большой однозначно отсчитываемой дальности m1 должно быть большим.
Частоты повторения соответствующие этим числам, находятся следующим образом:
;
; 
.
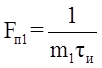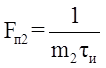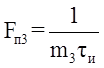Для определения однозначной дальности можно использовать теорему об остатках [2, т. 3 ]. Основанный на применении этой теоремы метод расчета позволяет вычислить истинную дальность Dо по трем номерам стробов дальности A1,A2,A3. Номер строба представляет собой дальность, выраженную в единицах длительности импульса.
Теорема для трех частот повторения имеет вид
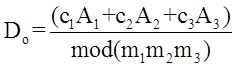. (27)
Это означает, что Dо равно остатку члена, заключенного в скобки, при делении его на m1, m2, m3 столько раз, сколько возможно. Следовательно, величина дальности лежит в пределах 1≤D≤ m1m2m3. Постоянные c1, c2, c3 связаны с m1, m2, m3 следующими уравнениями:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.