Открываем Maple и прописываем ввод исходной матрицы:
![]()
![]()
![]()
![]()
![]()
![]()
А далее строчки цикла, в котором, используя элементарные преобразования характеристической матрицы, получаем большое количество матриц с другими числовыми элементами, но имеющими строго такие же собственных значения, причем с той же кратностью.
![]()
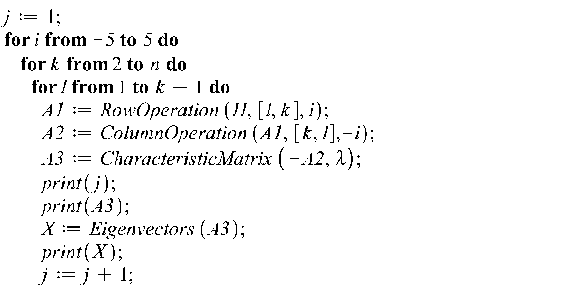
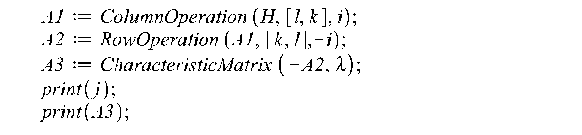
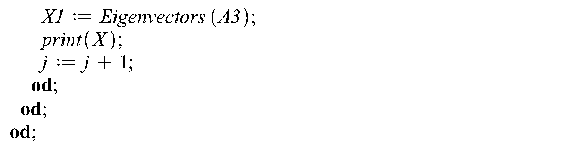
В результате выполнения этого кода получаем 66 различных матриц, из которых выбираем наиболее простые (например, элементы матрицы не превосходят заданного числа). Возьмем 5 матриц:
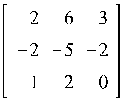
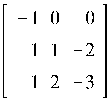
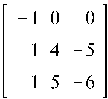
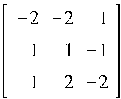
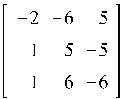
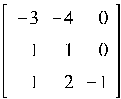
Все эти матрицы имеют собственные значения равные -1 с кратностью 3.
Если же необходимо из данной матрицы получить новые, но с уже другими собственными значениями, можно применить следующие строчки:
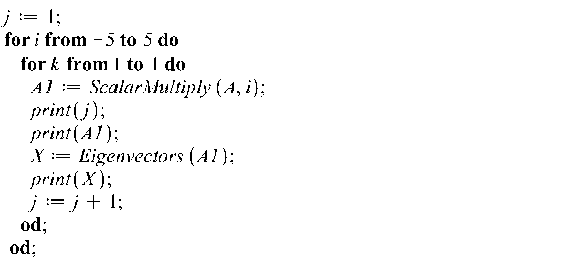
В результате выполнения этого блока кода, мы получаем 9 матриц с подобной структурой собственных значений, но с уже различными числовыми значениями. К примеру, вот 3 матрицы из них:
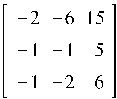 собственные значения :
собственные значения : ![]()
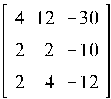 собственные значения :
собственные значения : ![]()
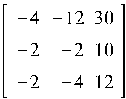 собственные значения :
собственные значения : 
Изменяя пределы внешнего цикла можно получить необходимое количество матриц.
Таким образом, взяв те же самые 5 известных примеров из пособий и выбрав затем по 5 и 3 матриц, полученных в результате выполнения алгоритма, мы получим 45 (5 исходных и 40 сгенерированных) различных матриц с пятью вариантами собственных значений, что уже вполне достаточно для индивидуальной работы.
Данный подход можно применять не только к задачам о собственных значений, но и ко многим задачам курса матричного анализа. Приведем еще один алгоритм генерации условий.
МП-матрица
![]()
![]()
![]()
![]()
Далее находим скелетное разложение исходной матрицы и находим псевдообратную матрицу:
![]()

![]()
![]()
В следующем фрагменте происходит генерация новых матриц с другим скелетным и с другой МП-матрией:
![]()

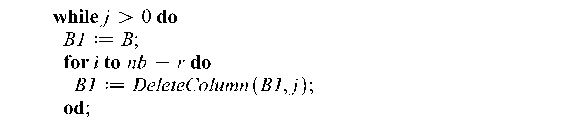

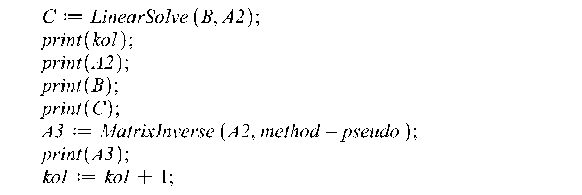

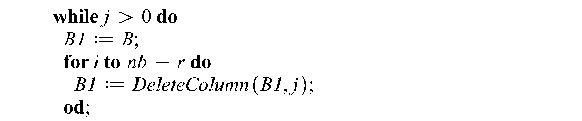


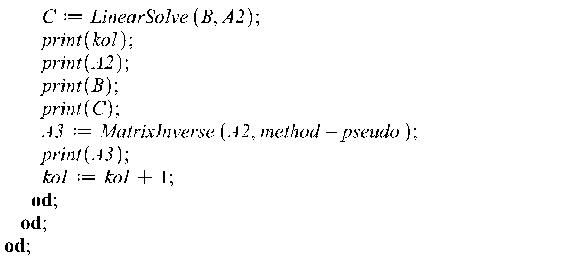
В результате работы данного алгоритма решена проблема генерации условий для МП-матриц.
Краткий обзор функций пакета LinearAlgebra
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.