RowOperation(A, K) (ColumnOperation(A, K)) - функция, где K - список из двух чисел, возвращающая матрицу, у которой переставлены строки (столбцы), соответственно числам в списке K:
Пример 5.5. Переставить местами 1-ую и 2-ую строки матрицы A, где
A
= 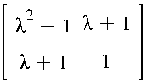
![]()
![]()
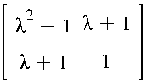
![]()
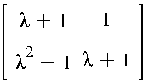
Умножение строки (столбца) на алгебраическое выражение
RowOperation(A, K, s) (ColumnOperation(A, K, s)) - функция, где К – целое число, возвращающая матрицу, у которой К-ая строка (столбец) умножена на s:
Пример 5.6. Дана матрица A
= 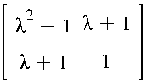
1) умножить 2-ую строку матрицы A на 2.
2) умножить 2-ой столбец матрицы A на λ.
![]()
![]()
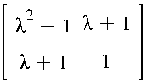
![]()

![]()
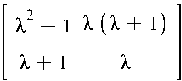
Прибавление к одной из строк (столбцов) другой строки (столбца)
RowOperation(A, K, s) - функция, где К – список из двух целых чисел i1 и i2, возвращающая матрицу, у которой строка i1 заменена на сумму Row(A, i1) + s∙Row(A, i2).
Аналогично ColumnOperation(A, K, s) возвращает матрицу, у которой стобец i1 заменен на сумму Column(A, i1) + s∙Column(A, i2):
Пример
5.7. Умножить 2-ую строку матрицы A
на 2 и прибавить к 1-ой, где A = 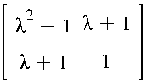
![]()
![]()
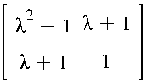
![]()
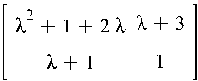
Жорданова нормальная форма матрицы
Определение 6.1. Квадратные матрицы A и B, одного и того же порядка, называются подобными, если существует такая невырожденная матрица C, что имеет место равенство A = C-1BC.
Пример 6.1. Проверить, подобны ли матрицы A =  и B =
и B =

![]()
![]()

![]()

![]()
![]()
Рассмотрим квадратные матрицы порядка n над полем P.
Определение 6.2.
Жордановой
клеткой
порядка k относящейся к числу λ0 называется
матрица порядка k (где ![]() )
вида:
)
вида:
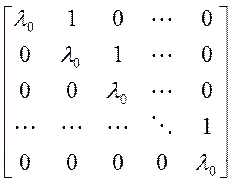
Примеры:
K=1;![]() ; K=2;
; K=2; 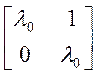 ; K=3;
; K=3; 
Определение 6.3. Жордановой матрицей порядка n называется матрица вида:
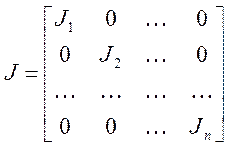
где J1, J2, …, Js - жордановы клетки.
Диагональные матрицы являются частным случаем жордановой матрицы, у них все жордановы клетки 1-го порядка.
Алгоритм приведения квадратной матрицы к жордановой нормальной форме:
Шаг 1. Находим все корни характеристического многочлена в матрице A и их кратности. Если хотя бы один корень не принадлежит полю P, то делаем вывод, что матрица не приводится к жордановой нормальной форме.
Шаг 2. Пусть λ - один из корней характеристического многочлена матрицы A и k - его кратность.
По формуле l(λ) = n – rang(A – λE) определяем общее число клеток жордана вида Jt(λ), t = 1, 2, ..., k.
Для ![]() по формуле
по формуле
lr(λ) = rang(A – λE)t + 1 – 2·rang(A – λE)t + rang(A – λE)t - 1 находим общее число клеток порядка t с элементом λ на главной диагонали входящих в матрицу жордана J. При этом (A – λE)0 = E.
Шаг 3. Повторяем второй шаг для всех корней характеристического многочлена матрицы A.
Шаг 4. Расставляем клетки жордана на главной диагонали матрицы J.
Пример
6.2. Найти Жорданову форму матрицы A,
где A=
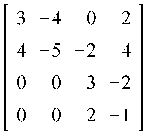
![]()
![]()

Шаг 1. Найдём корни характеристического многочлена:
Построим матрицу характеристического многочлена матрицы A равного: |A-vE|:
![]()
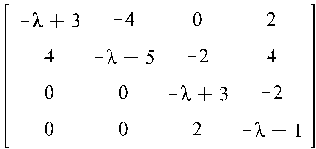
Запишем характеристический многочлен:
![]()
![]()
Найдём корни характеристического многочлена:
![]()

Определим размерность квадратной матрицы A:
![]()
![]()
![]()
Шаг 2. Определим число клеток Жордана:
Вычислим общее кол-во клеток:


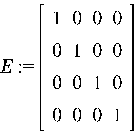
![]()
![]()
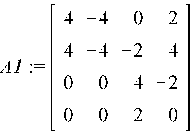
![]()
![]()
![]()
![]()
![]()

![]()
![]()
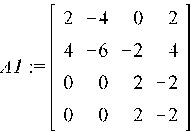
![]()
![]()
![]()
![]()
![]()
Шаг 3. Построим по полученным данным Жорданову нормальную форму исходной матрицы:
(построение производится вручную)
![]()
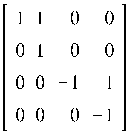
Шаг 4. Проверим результат:
![]()

Примечание: Матрицы J и J1 равносильны. Так как одна сводится к другой при помощи элементарных преобразований.
Пусть имеется матрица A ![]() Cn,n и функция f
: C→ C. Требуется
определить f(A).
Cn,n и функция f
: C→ C. Требуется
определить f(A).
В частном случае когда ![]() - многочлен относительно x,
f(A) мы находим непосредственной подстановкой:
- многочлен относительно x,
f(A) мы находим непосредственной подстановкой:
![]()
Пусть ψ(λ) - минимальный многочлен матрицы A.
![]() ,
,![]() ,
,
где - все различные собственные значения матрицы A.
Пусть имеются два многочлена g(λ) и h(λ), такие, что g(A) = h(A), тогда d(λ) = g(λ) – h(λ) – аннулирующий многочлен матрицы (так как d(A) = g(A) – h(A) = 0) и, значит, делится на ψ(λ) без остатка.
Следовательно,
![]() ,
, ![]() , … ,
, … , ![]() ,
, ![]()
Значит,
![]() ,
, ![]() , … ,
, … , ![]() ,
, ![]()
Множество, состоящее из m чисел:
![]() ,
,
будем называть значениями функции f на спектре матрицы A. Если они существуют, то будем говорить, что функция f определена на спектре матрицы A. Если функция f не определена на спектре матрицы A, то не определено и f(A).
Мы показали, что если g(A) = h(A), то g(ΛA) = h(ΛA). Нетрудно заметить, что верно и обратное, то есть если g(ΛA) = h(ΛA), то g(A) = h(A).
Отсюда следует, что значения многочлена g на спектре матрицы A однозначно определяют матрицу g(A), то есть все многочлены, значения которых на спектре матрицы A совпадают с g(ΛA), будут иметь матричное значение g(A).
Таким же образом определим произвольную функцию матричного аргумента: значения функции f(λ) на спектре матрицы A должны полностью определять f(A), то есть все функции, значения которых на спектре матрицы A совпадают, должны иметь одно и то же матричное значение f(A). Но тогда, для того чтобы найти f(A), достаточно найти любой многочлен g(λ), который на спектре матрицы A принимал бы те же значения, что и функция. Тогда f(A) = g(A).
Определение 7.1. Пусть функция f определена на спектре матрицы A, тогда f(A) = g(A), где g(λ) - любой многочлен, такой, что f(ΛA) = g(ΛA).
Но всегда можно добиться того, что степень многочлена, с помощью которого мы определяем f(A), будет меньше m. Действительно, разделим g(λ)на ψ(λ):
g(λ) = ψ(λ) q(λ) + r(λ), где deg r < m.
Тогда g(A) = ψ(A) q(A) + r(A), но ψ(A) = 0, следовательно, g(A) = r(A), значит f(A) = r(A).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.