<имя переменной>, <выражение2>, <последовательность операторов> - имеют равносильные определения, предложенные в первом формате конструкции.
<выражение1> - множество значений, которые принимает переменная.
Пример 1.10. Сумма элементов из множества {1, x, y, z2, 5}

![]()
Не стоит думать, что вышеперечисленными базисными конструкциями языка возможности Maple ограничиваются. Программирование в среде Maple также предусматривает чтение и запись данных в файл, создание собственных процедур и функций, а затем помещение их в собственную библиотеку (пакет). В случае возникновения ошибок в исходном коде можно воспользоваться встроенным отладчиком. В случае надобности, полученный исходный код можно перекодировать на распространённые языки Си и Фортран. И хотя распространенность второго явно преувеличена, это, в общем и целом, делает язык программирования Maple универсальным инструментом, который подходит для создания как простых, так и действительно сложных и объёмных вычислительных программ, легко транслируемых на другие языки.
1.4 Пакеты
Система Maple сама по себе является эффективным центром управления вычислениями. Но всё же большинство функций загружается не при запуске программы, а при инициализации так называемых пакетов. Эти пакеты содержат в себе группу дополнительных возможностей (команд), реализованных посредством функций и процедур, и легко читаемых Maple. Это сделано не только для экономии памяти, но и для того чтобы функции из разных разделов математики не смешивались между собой. Удобная специализация и структура пакетов избавляет вашу работу от постоянных поисков нужной функции, среди того огромного количества функций присутствующих в Maple (а их, как уже упоминалось, больше двух тысяч).
Например, чтобы загрузить функции для задач линейной алгебры и векторного исчисления, введите следующую команду:
Пример 1.11. Подключение пакета LinearAlgebra
![]()
Для того чтобы отобразить список, загружаемых при этом функций, завершите команду точкой с запятой. Таким же образом инициализируются и все другие пакеты.
Особого внимания за свои возможности заслуживает пакет Student. Как не трудно догадаться из названия, он предназначен для студентов-математиков. Он содержит в себе основные пакеты для вычислений, такие как Calculus1, VectorCalculus. А также пакет LinearAlgebra, которому в основном и посвящена эта книга.
Нами были выбраны пакеты LinearAlgebra и linalg для разработки алгоритмов работы над матрицами. Эти пакеты позволяет выполнять все основные действия над матрицами. В пакете LinearAlgebra, в отличие от устаревшего уже linalg, была сделана ставка на использование давно апробированных быстрых алгоритмов линейной алгебры, предложенных создателями Number Algorithm Group (NAG). Как ни парадоксально, но всё же не все функции из linalg были перенесены в пакет LinearAlgebra, поэтому списывать его со счетов не стоит. В дальнейшем мы будем обращаться к этим функциям, но предварительно обговаривая, что они находятся только в пакете linalg.
При решении сложных задач Вам вероятнее всего потребуются новые специфические функции, которые Вы и найдете в других пакетах. В приложении 3 предоставлен список всех пакетов системы Maple, включая новые пакеты появившиеся только в 11 версии. Для их более детального рассмотрения советуем обратиться к приведённой в конце книги литературе.
На этом вводная часть заканчивается и мы приступаем к изучению курса матричного анализа. При соответствующей математической подготовке приведённых выше фундаментальных знаний о Maple должно хватить для самостоятельного изучения всех пакетов этой системы. Мы же в нашем пособии остановимся только на пакетах LinearAlgebra и linalg, но сделаем это максимально подробно.
Определение 2.1. Матрица (лат. matrix - источник, начало) - прямоугольная таблица, образованная из чисел (обычно действительных или комплексных), состоящая из m строк и n столбцов.
Обозначение:
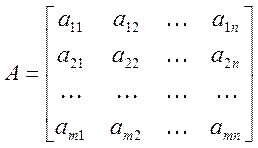
Числа aij (![]() ;
;![]() ), составляющие данную матрицу, называются
ее элементами. Здесь первый индекс i обозначает номер строки элемента, а второй j— номер его столбца. Причем говорят, что
матрица A имеет тип m
), составляющие данную матрицу, называются
ее элементами. Здесь первый индекс i обозначает номер строки элемента, а второй j— номер его столбца. Причем говорят, что
матрица A имеет тип m![]() n.
n.
Для матрицы A часто употребляется сокращенная запись:
A = [ aij ] или A = [ aij ]m,n,
где aij (![]() ;
;![]() ).
).
Пример 2.1. Ввод матрицы в Maple двумя способами
![]()
![]()

![]()

Если т
= п, то матрица называется квадратной порядка п. Если же т ≠ п, то
матрица называется прямоугольной. В частности, матрица типа 1![]() n называется вектором-строкой, а
матрица типа m
n называется вектором-строкой, а
матрица типа m![]() 1 - вектором-столбцом. Число
(скаляр) можно рассматривать как матрицу типа 1
1 - вектором-столбцом. Число
(скаляр) можно рассматривать как матрицу типа 1![]() 1.
1.
Определение 2.2. Диагональной называется квадратная матрица вида:
B
= 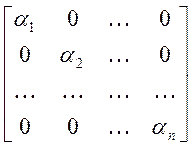
Сокращённая
запись: B = [ ![]() ]
]
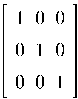
Если в диагональной
матрице все ![]() = 1 (
= 1 (![]() ), то такая матрица называется единичной и
обозначается буквой Е.
), то такая матрица называется единичной и
обозначается буквой Е.
Пример 2.2. Ввод единичной матрицы
![]()
![]()
Определение 2.3. Cуммой (разностью) двух матриц A = [ аij ] и B = [ bij ] одинакового типа называется матрица C= [ cij ] того же типа, элементы которой cij= аij+ bij(cij= аij– bij).
Пример 2.3. Разность между матрицей A из примера 2.1 и матрицей B из примера 2.2
![]()

Непосредственно из предыдущего определения вытекают следующие ее свойства сложения матриц:
1) A + (B + C) = (A + B) + C − ассоциативность.
2) A + B = B + A − коммутативность.
3) A + 0 = A − свойство нуля.
Определение 2.4. Произведением матрицыA = [ аij]на число α (или произведением числа α на матрицу A) называется матрица, элементы которой получены умножением всех элементов матрицы A на число α.
Пример 2.4. Найти произведение матрицы A на число α, где
A=  , а α= 3
, а α= 3
![]()
![]()

![]()
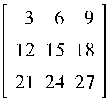
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.