Определение
2.5. Пусть A = [ аij]и
B = [ bij]матрицы типов соответственно
m![]() nи p
nи p![]() q. Если
число столбцов матрицы A равно числу строк матрицы B, т. е. п
= р, то для этих матриц определена матрица C типа m
q. Если
число столбцов матрицы A равно числу строк матрицы B, т. е. п
= р, то для этих матриц определена матрица C типа m![]() q называемая их произведением, при этом cij = аi1b1j +
аi2b2j + … + ainbnj , (
q называемая их произведением, при этом cij = аi1b1j +
аi2b2j + … + ainbnj , (![]() ;
; ![]() ).
).
Из определения вытекает следующее правило умножения матриц:
Чтобы получить элемент, стоящий в i-й строке и j-м столбце произведения двух матриц, нужно элементы i-й строки первой матрицы умножить на соответствующие элементы j-го столбца второй и полученные произведения сложить.
Мнемоническое правило:Cтрока на столбец.
Пример 2.5. Найти произведение матриц A и B, где
A=  , B=
, B= 
![]()
![]()
![]()


![]()
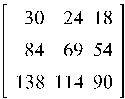
Или
![]()
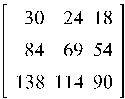
Произведение AB имеет смысл тогда и только тогда, когда матрица A содержит в строках столько элементов, сколько элементов имеется в столбцах матрицы B. В частности, можно перемножать квадратные матрицы лишь одинакового порядка.
Произведение двух матриц не обладает переместительным свойством, т. е., вообще говоря, AB ≠ B A, в чем можно убедиться на примерах.
Более того, может даже случиться, что произведение двух матриц, взятых в одном порядке, будет иметь смысл, а произведение тех же матриц, взятых в противоположном порядке, смысла иметь не будет.
В тех частных случаях, когда AB = BA, матрицы A и B называются перестановочными (коммутативными). Так, например, как нетрудно убедиться, единичная матрица Е перестановочна с любой квадратной матрицей A того же порядка, причем AЕ = ЕA = A. Таким образом, единичная матрица Е играет роль единицы при умножении.
2.3 Определитель матрицы. Обратная матрица
Определение 2.6. Определителемили детерминантом квадратной матрицы A = [ аij ] называется число det A или |A|, которое может быть вычислено по элементам матрицы с помощью следующей рекурсии:
Если n = 1, то det A = a11;
Если n = 1, то det A = 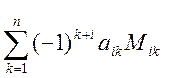 , где
, где ![]() .
.
Мik – детерминант матрицы, полученной из исходной вычеркиванием первой строки и k – го столбца.
Следует обратить внимание на то, что определители имеют только квадратные матрицы, т.е. матрицы, у которых число строк равно числу столбцов.
Пример 2.6. Найти определитель для матрицы A,
где A = 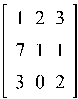
![]()
![]()

![]()
![]()
Определение 2.7. Минором элемента aij матрицы называется определитель матрицы, полученной из данной в результате вычеркивания i-й строки и j-гo столбца.
Определение 2.8. Рангом матрицы A называется такое натуральное число r, что среди всех миноров r-го порядка матрицы A есть хотя бы один не равный нулю, а все миноры (r + 1)-го порядка, если существуют, равны 0.
Пример 2.7. Найти ранг для матрицы A, где A=
![]()
![]()

![]()
![]()
Определение 2.9. Обратной матрицей по отношению к данной называется матрица, которая, будучи умноженной как справа, так и слева на данную матрицу, дает единичную матрицу.
Для матрицы A обозначим обратную ей матрицу через A-1. Тогда по определению имеем: AA-1 = A-1A = Е, где Е— единичная матрица.
Нахождение обратной матрицы для данной называется обращением данной матрицы.
Пример
2.8. Найти обратную
матрицу A-1 , где A = 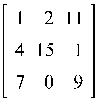
![]()
![]()
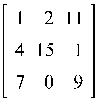
![]()
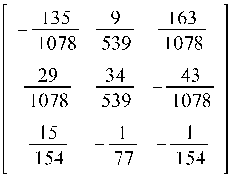
Блочные матрицы и их алгебра
Часто приходится пользоваться матрицами, разбитыми на прямоугольные части – «клетки» или «блоки».
Пусть дана прямоугольная матрица
![]()
При помощи горизонтальных и вертикальных линий рассечем матрицу A на прямоугольные блоки:
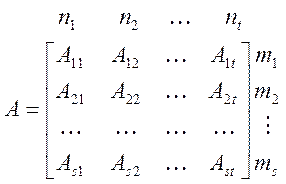
Про
эту матрицу будем говорить, что она разбита на s![]() tблоков Aαβразмером mα
tблоков Aαβразмером mα![]() nβ(
nβ(![]() ;
;![]() )
или что она представлена в виде блочной матрицы.
)
или что она представлена в виде блочной матрицы.
Сокращённая запись: A=
[ Aαβ ] (![]() ;
;![]() ).
).
Действия над блочными матрицами производятся по тем же формальным правилам, как и в случае, когда вместо блоков имеем числовые элементы.
Известно, что при умножении двух прямоугольных матриц A и B длина строк в первом сомножителе A должна совпадать с высотой столбцов во втором сомножителе B. Для возможности «блочного» умножения матриц дополнительно требуется, чтобы при разбиении на блоки все горизонтальные размеры в первом сомножителе совпадали с соответствующими вертикальными размерами во втором сомножителе:
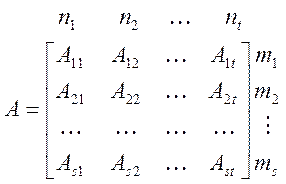 ,
,
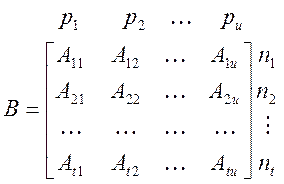
Тогда легко проверить, что
AB = C = [ Cαβ ], где
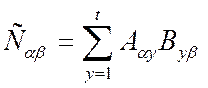
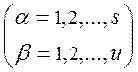
Заметим, что умножение квадратных блочных матриц одного и того же порядка всегда выполнимо, когда сомножители разбиты на одинаковые квадратные схемы блоков и в каждом из сомножителей на диагональных местах стоят квадратные матрицы.
Формула Фробениуса. Пусть неособенная квадратная матрица М (|M| ≠ 0) разбита на блоки
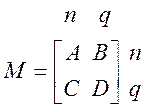 ,
,
и пусть также A – неособенная квадратная матрица (|A| ≠ 0) . Тогда матрица М-1 находится по формуле:
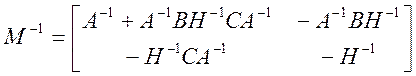 , где
, где ![]() .
.
Формула
Фробениуса сводит обращение матрицы порядка n+ q к обращению
двух матриц порядка nи
q и к
операциям сложения и умножения матриц с размерами n![]() n, q
n, q![]() q, n
q, n![]() q, q
q, q![]() n.
n.
Пример 3.1. Найти обратную матрицу M-1 по формуле Фробениуса, где
M = 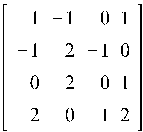
![]()
Ввод осуществляется посредством задания 4 блоков, на которые разбивается исходная матрица M
![]()
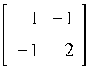
![]()
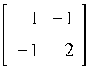
![]()
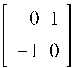
![]()

Далее вычисляем матрицу H и каждый блок матрицы M-1:
![]()
![]()
![]()
![]()
![]()
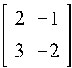
![]()
![]()
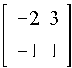
![]()
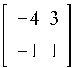
![]()
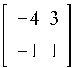
![]()
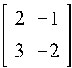
Далее формируем искомую матрицу M-1:
![]()
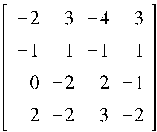
Функция
blockmatrixсодержится
в пакете linalg, поэтому для ее использования записывают выражение linalg[blockmatrix], что не подключает весь пакет, а дает возможность
использовать только одну функцию. Эта функция позволяет составить матрицу из
блоков размера n![]() n и q
n и q![]() q.
q.
Декомпозицию блоков можно сделать используя функцию SubMatrix, которая выделяет из матрицы заданный блок.
Пример
3.2. Разбить
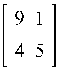
матрицу A на 4 блока, где A = 
![]()
![]()

![]()
![]()
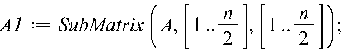
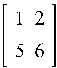
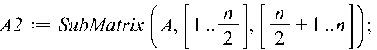

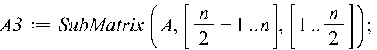
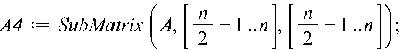

Собрать обратно блоки можно многими способами. Приведем два из них:
Пример 3.3. Составить матрицу из 4 блоков A1, A2, A3, A4,
где A1 = 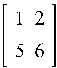 , A2 =
, A2 =  , A3 =
, A3 =  , A4 =
, A4 =  .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.