Основания и фундаменты транспортных сооружений: Электронный учебник, страница 27

(4.22)

          Коэффициенты приведенных уравнений определяются бесконечными рядами в зависимости от приведенной глубины рассматриваемой точки   [4]:

» »1 - (1- (1- (1- / 116280) / 32760) / 5040) / 120 +» »  (1 - (1- (1 -  / 43680) / 7920) / 360) » »2 (1 - (1 - (1 - / 57120) / 11880) / 840) / 2 » »3 (1- (1 - (1 -  / 73440) / 17160) / 1680) / 6

(4.23)

          Таким образом, система уравнений (4.23) позволяет определить горизонтальное перемещение сваи , поворот ее сечения , а также внутренние усилия - изгибающий момент  и поперечную силу  в сечении на произвольной глубине , если известны значения данных параметров в уровне поверхности грунта: , ,  и .

          Заметим, что при расчете свайного фундамента с низким ростверком глубина отсчитывается не от поверхности грунта, а от подошвы ростверка.

          Как правило, исходными данными для расчета деформаций сваи являются нагрузки и . Чтобы воспользоваться решением (4.23) нужно найти величины  и . Эти величины определяются зависимостями:

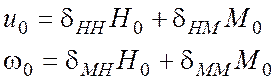                                                                                      (4.24)

          Перемещения сваи в уровне поверхности грунта от единичных усилий -   (рис. 4.30) даются выражениями:

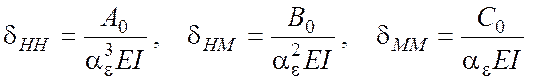                                              (4.25)

Рис. 4.30. Перемещения сваи в уровне поверхности грунта от  единичных усилий

          Для определения коэффициентов ,  и  принимаются следующие граничные условия [4]:

          1). для висячей сваи в уровне ее нижнего конца принимают равными нулю внутренние усилия:  и . Индекс «» здесь будет означать, что рассматриваемая величина определяется для глубины . Далее, из третьего и четвертого уравнений системы (4.22) получаются следующие выражения для искомых коэффициентов:

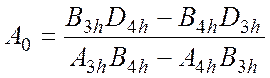
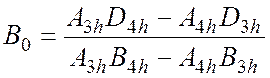                                                                                         (4.26)

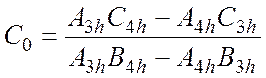
          2). при опирании сваи на скалу (свая-стойка): , . Из первого и третьего уравнения системы (4.22):

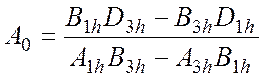
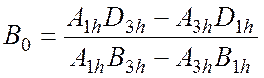                                                                                          (4.27)

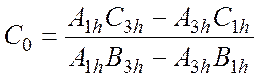
          3). при заделки сваи-стойки в скалу: , 0. Первое и второе уравнения системы (4.22) приводят к выражениям:

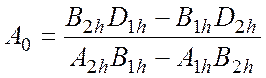
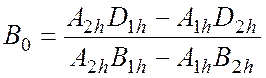                                                                                          (4.28)

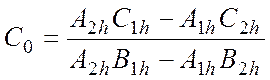
          Далее, рассмотрим сваю, имеющую свободную длину, и нагруженную поперечной силой и моментом  в уровне верхнего сечения. Запишем выражения для перемещений  и  этого сечения:

(4.29)

          Перемещения сваи в уровне верхнего сечения от единичных усилий -  (рис. 4.31) определяются с помощью решений (4.24) и решения строительной механики об изгибе консоли:

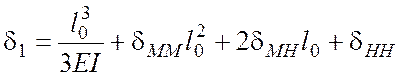
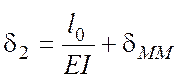                                                                                                      (4.30)

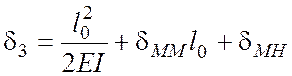
          Таким образом, приведенные в этом параграфе выражения позволяют рассчитать деформирование одиночной сваи в грунте, представленном упругой средой, описываемой с помощью гипотезы коэффициента постели, от действия горизонтальной и моментной нагрузок.

Рис. 4.31 Перемещения сваи в уровне подошвы плиты ростверка от  единичных усилий

                                  4.6.3 Характеристики жесткости сваи.

          Характеристиками жесткости сваи называются реакции верхнего сечения сваи (в уровне подошвы ростверка ) на единичные ее перемещения (рис. 4.32).

Рис.4.32  Реакции от единичных перемещений сваи (характеристики жесткости сваи)

          Рассмотрим нормальное (вдоль оси сваи) единичное перемещение. В этом случае реакция сваи представляется нормальной силой , направленной вдоль оси сваи. Эта реакция принимается равной [4, 6, 7]:

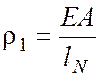                                                                                                                 (4.31)

где  - жесткость сваи на сжатие;  - расчетная длина сжатия сваи.

          Расчетная длина сжатия сваи  - это условная величина, обозначающая такую длину сваи, при которой ее сжатие как материального стержня приблизительно равно перемещению сваи с учетом как сжатия самой сваи реальной длины, так и величины вдавливания сваи в грунт. Естественно, для сваи-стойки расчетная длина  равна ее фактической длине:

                                                                                                             (4.32)

          Для висячих свай расчетная длина на сжатие устанавливается по эмпирической формуле:

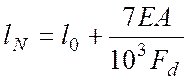                                                                                                    (4.33)

          И, наконец, для оболочек и столбов больших диаметров величина  определяется формулой:

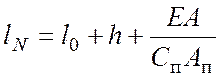                                                                                                (4.34)

где  - коэффициент постели грунта, залегающего в основании сваи;  - площадь поперечного сечения подошвы сваи (с учетом уширения при его наличии).

          Поперечное единичное перемещение сваи вызывает ответную реакцию в виде поперечной силы  и момента . Эти величины устанавливаются с помощью системы уравнений (4.29), в которых следует положить  и 0. Тогда, реакции  и   составят:

(4.35)

          Единичный поворот сечения вызовет ответную реакцию сваи в виде поперечной силы  и момента . Из системы (4.29), соответственно, следует выражение для :

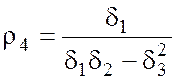                                                                                                      (4.36)

          Выражения для характеристик жесткости сваи используются при построении метода расчета свайного фундамента как многостоечной рамы, защемленной в упругом полупространстве - грунтовой среде, описываемой с помощью гипотезы коэффициента постели.

                              4.6.4 Каноническая система уравнений