Основания и фундаменты транспортных сооружений: Электронный учебник, страница 26

4.6 Расчет свайных фундаментов как стержневых систем

4.6.1. Расчетная схема свайного фундамента.

          Прежде, чем изучать проверки свайного фундамента по предельным состояниям, необходимо познакомиться с расчетом свайного фундамента как стержневой системы. Этот расчет предназначен для определения перемещений плиты ростверка, внутренних усилий по длине каждой сваи, а также для определения бокового давления свай на грунт. Для определения напряженно-деформированного состояния  элементов свайного фундамента формируется его расчетная  схема. Наибольшее практическое применение имеет плоская расчетная схема, но при необходимости расчет может выполняться и для пространственных условий [4].

          Рассмотрим плоскую расчетную схему свайного фундамента. На рис. 4.28   изображен свайный фундамент с высоким ростверком.

Рис. 4.28 К построению плоской расчетной схемы свайного фундамента

          Прежде всего, задается плоскость, например , действия внешних нагрузок, приведенных к какой-либо точке (как правило, к центру) подошвы плиты ростверка . На эту плоскость проецируется свайный фундамент в следующем виде. Плита ростверка представляется жестким недеформируемым ригелем и изображается в уровне ее подошвы () отрезком прямой жирной линии, совпадающей с осью . Сваи рассматриваются как гибкие стержни и изображаются в виде проекций их осей на плоскость  отрезками тонких линий. Если в одну и ту же проекцию попадает несколько свай, то в дальнейшем учитывается работа каждой из них в отдельности. Сваи, рассматриваемые как гибкий упругий стержень характеризуются площадью поперечного сечения , моментом инерции поперечного сечения  и модулем упругости материала сваи .           Уровень планировки обозначается прямой линией на соответствующей ему отметке . 

          Грунтовое основание считается упругим линейно-деформируемым в соответствии с гипотезой коэффициента постели. Гипотеза коэффициента постели принимается для установления линейной связи между поперечным перемещением грунта и давлением на него (рис.4.29).  Кроме того, принимается, что коэффициент постели линейно увеличивается с глубиной в соответствии с выражением:

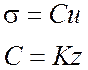                                                                                                                  (4.13)

где  - коэффициент постели;  - коэффициент пропорциональности для определения коэффициента постели; - расстояние от уровня планировки () для свайного фундамента с высоким ростверком и от уровня подошвы плиты ростверка () для свайного фундамента с низким ростверком;  - боковое давление сваи на грунт; - горизонтальное перемещение грунта.

Рис. 4.29. Гипотеза коэффициента постели

          Назначение коэффициента пропорциональности  производится по определенным правилам. Вначале устанавливается расчетная глубина , отсчитываемая от  (высокий ростверк) или от  (низкий ростверк):

                                                                                      (4.14)

          Если в пределах этой глубины расположен один слой грунта, то коэффициент пропорциональности принимается в зависимости от вида этого грунта. Для двух видов грунтов величина  устанавливается по формуле:

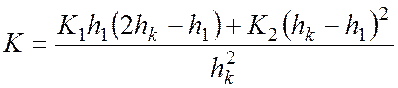                           ,                                 (4.15)

          Для трех слоев грунта используется выражение:

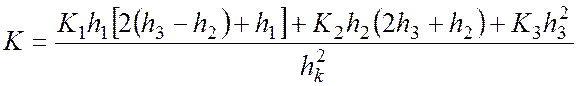                                   (4.16)

где - толщина первого, второго и третьего слоев грунта;  - коэффициенты пропорциональности для первого, второго и третьего слоев грунта.

          В заключении отметим, что положение -той сваи в расчетной схеме свайного фундамента характеризуется координатой  и углом наклона к вертикали  в соответствии с принятой системой координат . Положительные направления координат  и   обозначены на см. рис. 4.28.

4.6.2 Теоретические основы расчета свайного фундамента

как стержневой системы

          Методика расчета свайного фундамента основана на решении задачи о деформировании сваи в грунтовой среде под действием нагрузок, приложенных в уровне поверхности грунта. Рассмотрим случай, когда внешние нагрузки лежат в одной плоскости. Представляя сваю в виде упругого стержня для него записывают дифференциальное уравнение изогнутой оси [4]:

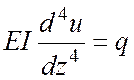                                                                                                  (4.17)

          Изгиб сваи обусловлен действием поперечной силы  и момента  приложенных в уровне поверхности грунта. Нагрузка  характеризует горизонтальный отпор грунта и определяется согласно гипотезе коэффициента постели:

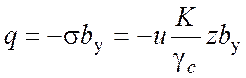                                                                                   (4.18)

где - коэффициент условия работ;  - условная ширина сваи.

          Параметры    и    позволяют приближенно учесть пространственные условия работы сваи в грунте. Условная ширина сваи  принимается равной м при диаметрах сваи  0,8 м , и  м  для меньших диаметров. Коэффициент условия работ принимается равным  при специальном учете пластического разрушения грунта около сваи, и  , если это явление не учитывается. Указанные значения  и   установлены на основе сопоставления расчетных величин перемещений сваи и их опытных значений.

                    Уравнение (4.17) записывается в виде:

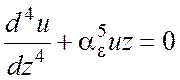                                                                                              (4.19)

          Параметр  называется коэффициентом деформации сваи и рассчитывается по формуле:

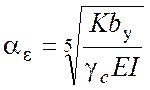                                                                                                  (4.20)

          Решение уравнения (4.19) было дано И.В.Урбаном и предназначалось для расчета шпунтовой стенки в условиях плоской деформации.

          Заметим, что при изгибе упругого стержня справедливы следующие зависимости:

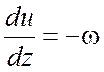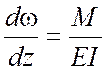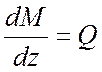                                            ;    ;                         (4.21)

          Решение И.В.Урбана с учетом приведенных выражений (4.21) дает следующую систему уравнений, определяющую работу сваи в грунте [4]: