Четырехосный крытый грузовой вагон, страница 6

       f_ст = 0,05 м – статический прогиб рессорного подвешивания для тележки ЦНИИ-Х3.

Р_g = 214,21 • 0,282 = 60,41 кН

    Вертикальная составляющая от сил инерции при торможении или ударе в автосцепку:

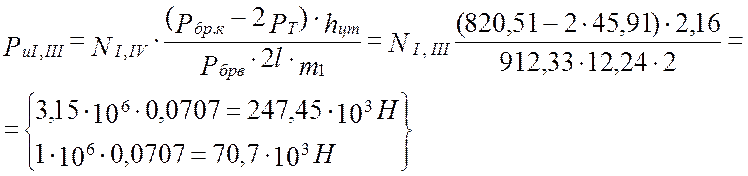              (3)

 Принимаем Р_и = 247, 45 кН как максимальную силу.

N_I = 3,5 •10⁶ Н – норма продольного усиления, принимаемая в расчетах по I режиму;

N_III - 10⁶ Н – норма продольного усиления, принимаемая в расчетах по III режиму;

Р_бр.к = m_брк • g = 83640 • 9,81= 820, 51 •10³ Н – сила тяжести где m_брк = 83640 кг – масса кузова вагона;

Р_т = m_т • g = 4680 кг • 9,81м/с² = 45,91 •10³ Н – сила тяжести тележки ЦНИИ-Х3 где  m_т = 4680 кг – масса тележки;

h_цт = 2 + 0,475 – 0,188 – 0,12 = 2,167 м – высота от опорной плоскости нижней балки проема тележки до центра масс кузова;

2 l = 12,24 м – база вагона;

m₁ = 2 – число параллельно нагруженных рам под одним концом вагона.

    Вертикальная составляющая от действия центробежной и ветровой нагрузок

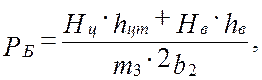                                            (4)

где Н_ц ≈ η_ип  •  Р_ст = 0,075 •  214,21 = 16,07 • 10³ Н – центробежная нагрузка,

 действующая на раму;

     η_ип = 0,075 – коэффициент, учитывающий непогашенную центробежную силу в кривых участках пути с учетом возвышения наружного рельса;

    2b₂ = 2,036м – расстояние между серединами шеек оси или точками дополнительного загружения и разгружения продольных осей боковых рам;

    m₃ = 2 – количество боковых рам, расположенных с одной стороны вагона;

    Н_в = ω  •  F = 500 • 53,4 = 26,7• 10³ Н – ветровая нагрузка, действующая на раму, где ω = 500 Н/м²,  F = 53,4 м²;

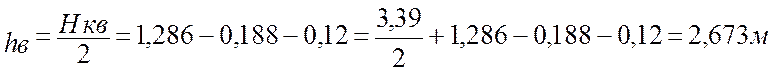    – высота от опорной плоскости нижней балки проема тележки до центра приложения ветровой нагрузки.

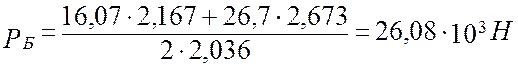
    Определим общую нагрузку:

Р = Р_ст + Р_g + Р_и + Р_б                                                  (5)

Р = 21,21 + 60,41 + 247,45 + 26,08 = 548,15 кН

  Изобразим боковую раму тележки и укажем размеры ее поперечных сечений в нескольких местах:

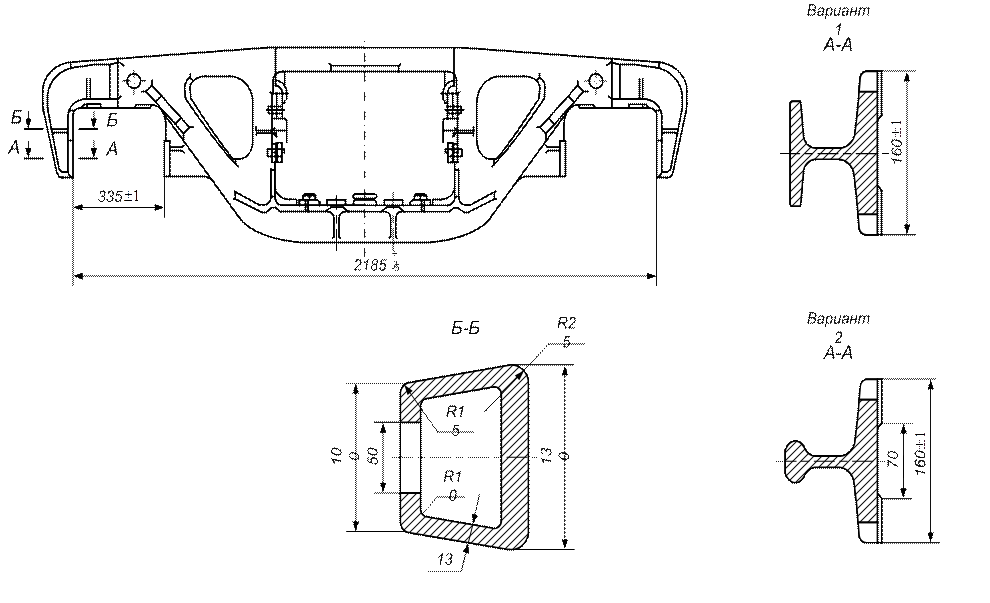
    Симметричность конструкции на рис. 1 и загружения относительно поперечной вертикальной плоскости, проходящей через середину рамы позволяет рассматривать одну половину рамы, которая будет 5 раз статически неопределенной.

   Расчет произведем методом сил:

δ₁₁ • х₁ + δ₁₂ •  х₂ + δ₁₃ • х₃ + δ₁₄ • х₄ + δ₁₅  • х₅ + ∆_1р = 0;

δ₂₁ • х₁ + δ₂₂ •  х₂ + δ₂₃ • х₃ + δ₂₄ • х₄ + δ₂₅  • х₅ + ∆_2р = 0;

δ₃₁ • х₁ + δ₃₂ •  х₂ + δ₃₃ • х₃ + δ₃₄ • х₄ + δ₃₅  • х₅ + ∆_3р = 0;                      (6)

δ₄₁ • х₁ + δ₄₂ •  х₂ + δ₄₃ • х₃ + δ₄₄ • х₄ + δ₄₅  • х₅ + ∆_4р = 0;

δ₅₁ • х₁ + δ₅₂ •  х₂ + δ₅₃ • х₃ + δ₅₄ • х₄ + δ₅₅  • х₅ + ∆_5р = 0;

где δ_11, δ₁₂ ….. δ₅₅  - коэффициенты системы уравнений;

      ∆_1р, ∆_{2р ……..} ∆_5р – свободные члены.

    Коэффициенты и свободные члены находим перемножением соответствующих единичных эпюр М₁ , М_{2 ,} М_{3 ,} М_{4 ,} М₅ и эпюры М_g.

   Для выполнения коэффициентов и грузовых членов эпюры изгибающих моментов и поперечных и нормальных сил от неизвестных силовых факторов, равных выбранной единицы и внешней нагрузки.

   Далее вычислим характеристики каждого из указанных на рис. 1 сечений:

J_z – момент инерции сечения относительно оси z;

W_z – момент сопротивления сечения относительно оси z;

F – площадь сечения стержня.

Сечение 1-1:

J_z = 280,41 см² ; W_z = 52,41 см³; F = 51,12 см²

 Сечение 2-2,(3-3):

J_z = 222 см⁴ ; W_z = 39,57 см³; F = 38,87 см²

Сечение 4-4:

J_z = 3891,3 см⁴ ; W_z = 533,79 см³; F = 84,52 см²

Сечение 5-5:

J_z = 283,28 см⁴ ; W_z = 52,65 см³; F = 52,02 см²

   Коэффициенты системы канонических уравнений последовательно будем определять по формуле:

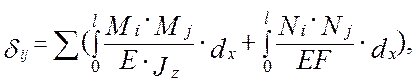                                             (7)

где Е = 2,06 • 10⁴ кН/см² – модуль упругости для стали.

δ₁₁ = 0,472;                                δ₂₄ = δ₄₂ = 60,89;                     ∆1Р = 197,96;

δ₁₂ = 2,42;                                  δ₂₅ = δ₅₂ = 34,43;                     ∆2Р = 10238,39;

δ₁₃ = δ₃₁ = - 0,09;                        δ₃₃ = 0,3;                                 ∆3Р = - 919,73;                            

δ₁₄ = δ₄₁ = 3,056;                        δ₃₄ = δ₄₃ = - 9,39;                     ∆4Р = 3035,44;

δ₁₅ = δ₅₁ = 1,834;                        δ₃₅ = δ₅₃ = - 2,64;                     ∆5Р = - 1615,15.

δ₂₁ = δ₅₁ = 2,42;                          δ₄₄ = 34,75;                              

δ₂₂ = 62,8;                                  δ₄₅ = δ₅₄ = 57,40;       

δ₂₃ = δ₃₂ = - 1,42;                        δ₅₅= 46,35;                                         

   Подставим найденные коэффициенты и свободные члены в систему уравнений и получаем систему уравнений следующего вида:

                  0,47 х₁ + 2,42  х₂ + (-0,09)  х₃ + 3,056  х₄ + 1,84 х₅ + 197,96 = 0;

2,42 х₁ + 62,8  х₂ + (-1,42) х₃ + 60,89 х₄ + 34,43 х₅ + 10238,39 = 0;

 - 0,09 х₁ + (-1,42) х₂ + 0,3 х₃ + (-9,39) х₄ + (-2,64) х₅ – 919,73 = 0;                        

3,056 х₁ + 34,43 х₂ + (-9,39) х₃ + 34,75 х₄ + 57,40  х₅ +3035,44 = 0;

                 1,84 х₁ + 34,43 х₂ + (-2,64) х₃ + 57,4 х₄ + 46,35 х₅ – 1615,15 = 0.

   Решая  систему уравнений  получим:

                   х₁ = 281,9; х₂ = - 251,81; х₃ = 1063; х₄ = - 160,9; х₅ = 470,49.

    Имея эпюры изгибающих моментов нормальных и поперечных сил определим напряженное состояние рамы в наиболее опасных сечениях и дадим оценку прочности рамы.

    Для стали 20 ГФЛ, из которой обычно отливают боковые  рамы предел текучести составляет δ_т = 314 мПа, тогда допускаемое нормальное напряжение для сечений рамы будет выражено как [δ] = 0,9 δ_т = 0,9 • 314 = 283 мПа и допускаемое напряжение среза будет выражено как [τ] = 0,5 δ_т = 0,5 • 314 = 157 мПа.

     Условие прочности для рамы тележки имеет вид: