
















Лекционные материалы (Теория подобия).
ОГЛАВЛЕНИЕ.
1. Теоремы подобия.
1.1. Первая теорема подобия.
1.2. Вторая теорема подобия.
1.3. Третья теорема подобия.
2. Условия осуществления подобия
2.1. Степенные комплексы.
2.2. Свойства степенных комплексов.
2.3. Условия осуществления подобия для простых уравнений.
3. Подобие уравнений общего вида.
3.1. Четвертое условие подобия.
3.2. Пятое условие подобия.
4. Процесс подобного моделирования.
4.1. Исходные данные, необходимые для подобного моделирования.
4.2. Этапы подобного моделирования.
4.2.1.1.1 Пример 1.
4.2.1.1.2 Пример 2.
5. Критерии подобия гидромеханических процессов
6. Критерии подобия для тепловых процессов
6.1. Передача тепла конвекцией
6.2. Теплоотдача при вынужденной конвекции
6.2.1. Движение теплоносителя по трубам и каналам
6.2.2. Теплоотдача при движении теплоносителя вне труб
6.2.3. Перемешивание жидкости мешалкой
6.2.4. Стекание жидкости пленкой
Теория подобия.
МАТЕРИАЛЫ.
Подобие в математическом моделировании.
Понятие о подобии зародилось в древности в геометрии. Геометрически подобными фигурами считались такие, которые имели одну и ту же форму и обладали свойством пропорциональности сходственных линейных размеров.
Позже, уже в средние века, понятие о подобии было распространено на физические явления. Позже стали говорить о тепловом подобии, кинематическом подобии, динамическом подобии и т.д.
Напомним определение подобия.
Подобие – это полная математическая аналогия при наличии пропорциональности между сходственными переменными, неизменно сохраняющаяся при всех возможных значениях этих переменных, удовлетворяющих сходственным уравнениям[1].
Подобные модели, обеспечивают перенос данных, полученных в результате исследования модели на оригинал, на основании подобия оригинала и модели.
Подобию во всех его видах свойственны некоторые общие закономерности, которые принято называть первойвторой и третьей теоремами подобия. Две первые теоремы устанавливают соотношения между параметрами подобных явлений, не указывая способов реализации подобия при построении моделей. Ответ на последний вопрос дает третья или обратная теорема подобия.
Сформулируем без доказательства перечисленные теоремы подобия.
Если явления подобны или физически или математически или в другом каком-либо смысле, то всегда из их параметров можно составить такие сочетания, что они будут одинаковы для обоих подобных явлений[2].
Безразмерные сочетания параметров, численно одинаковые для подобных явлений, носят название «Критерии подобия» или «числа подобия».
Из определения следует: из параметров подобных явлений всегда можно составить такие сочетания, что их отношения для подобных явлений будут равны единице.
Первая теорема может быть сформулирована и следующим образом: «равенство одноименных чисел подобия является следствием подобия физических явлений».
Всякое полное уравнение физического процесса, записанное в определенной системе единиц, может быть представлено зависимостью между критериями подобия, (то есть полное уравнение физического процесса может быть представлено уравнением, связывающим безразмерные величины, полученные из параметров, участвующих в процессе).[3]
Отметим, что данная теорема касается только процессов, отражаемых полными уравнениями и записанных в определенной системе единиц.
Значение этой теоремы заключается в том, что она указывает на возможность представить математическое описание физических явлений в виде функциональной зависимости между числами подобия, что придает анализу обобщенный характер. Таким образом, эта теорема указывает, как должны быть обработаны результаты экспериментов при изучении явления, а именно, они должны быть представлены в виде зависимости между безразмерными числами подобия, а не между отдельными размерными величинами.
Для подобия явлений - определяющие критерии подобия должны быть соответственно одинаковыми, а условия однозначности (краевые условия) подобны.[4]
Определим условия осуществления подобия для простых уравнений и уравнений в общем виде для случаев, когда последние имеют единственное, не единственное и неоднозначное решения.
Наиболее общие условия подобия уравнений можно сформулировать на базе понятия о степенных комплексах и их подобии.
Степенным комплексом называется функция вида
![]()
правая часть которой представляет собой произведение различных степеней постоянных или переменных величин xi, причем ai - любые числа.
Представим себе, что из N величин x1, x2, x3 …xN образовано n различных степенных комплексов
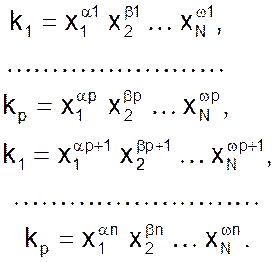
В общем случае все степенные комплексы можно подразделить на простые и составные.
Простыми степенными комплексами считаются такие, что ни один из них не может быть представлен в виде степенного комплекса, образованного из степенных комплексов этой группы.
С учетом данного определения, представленная нами группа степенных комплексов включает p – простых и (n - p) – составных комплексов.
Степенные комплексы могут иметь физическую размерность (сила есть масса, умноженная на ускорение) и быть безразмерными.
Степенные комплексы обладают несколькими свойствами, которые нужно учитывать при операциях с ними:
● Число простых степенных комплексов, образованных из нескольких величин, не может превзойти числа этих величин.
● Любую функцию некоторых величин можно представить в виде функции степенных комплексов этих величин.
● Любую безразмерную функцию размерных величин можно представить в виде функции безразмерных степенных комплексов, образованных из этих величин.
● Любую размерную функцию размерных величин можно представить в виде произведения размерного степенного комплекса, составленного из этих величин, и безразмерной функции этих же величин.
Как следует из определения подобия, оно может быть осуществлено, с одной стороны, при наличии полной математической аналогии между оригиналом и моделью, а с другой – при наличии пропорциональности между сходственными переменными оригинала и модели.
Установим на примере условия, при которых оригинал и его модель будут подобными.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.