В простейшем случае модель и оригинал могут быть описаны двумя сходственными уравнениями:
![]() (01)
(01)
![]() (02)
(02)
при этом (см. определение подобия) они будут подобны, если их сходственные переменные пропорциональны друг другу.
Назовем коэффициенты пропорциональности масштабами и обозначим для сходственных переменных через my и mx
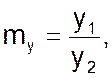 (03)
(03)
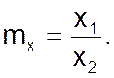 (04)
(04)
После ввода масштабов соотношения между y1 ,y2 ,x1 ,x2 определяются уже не двумя уравнениями 01 и 02 а четырьмя - 01, 02 и 03, 04 . Очевидно, что дополнительные уравнения 03, 04 должны быть такими, чтобы система уравнений в целом 01 - 04 не оказалась противоречивой.
Таким образом можно утверждать: необходимым для подобия функций 01 и 02 является условие непротиворечивости системы, содержащей как исследуемые сходственные уравнения, так и масштабные.
При условии непротиворечивости системы уравнений 01 и 02 можно:
● задавшись значением x1, определить y1 (двумя путями см. рис. a);
● задавшись значением x2 , определить y2 (двумя путями см. рис. b).
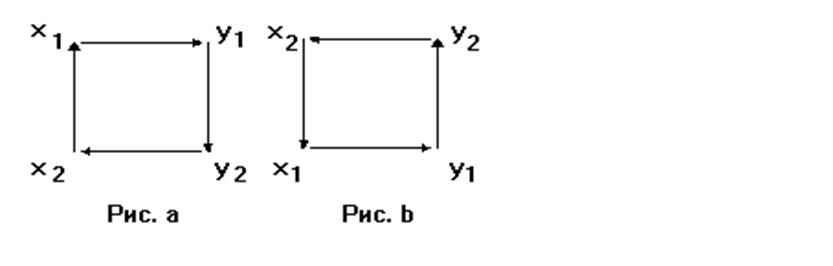
Используя первое уравнение.
Действуя прямым путем, по заданному x1 рассчитывают y1.
![]()
Действуя окольным путем, находят последовательность

и, наконец
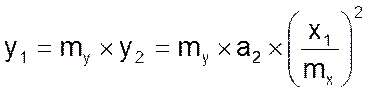 (05)
(05)
Система 01 - 04 непротиворечива, если уравнения 01 и 05 тождественны:
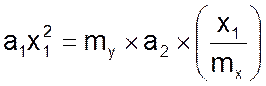
Условие непротиворечивости имеет вид
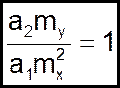 (06)
(06)
Обратим внимание. Полученное нами условие непротиворечивости представляет собой отношение двух безразмерных степенных комплексов
![]() и
и ![]() ,
,
и образует, в свою очередь, безразмерный степенной комплекс
![]() .
.
Используя второе уравнение,
Действуя прямым путем, y2 рассчитывают по заданному x2 .
![]()
Действуя окольным путем, находят последовательно
![]()
и, наконец рассчитывают y2
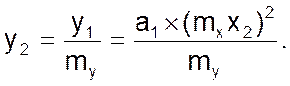 (07)
(07)
Система 01 - 04 непротиворечива, если выражения 02 и 07 тождественны:
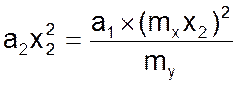
![]()
Из последнего уравнения следует условие непротиворечивости, которое имеет вид
![]()
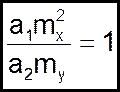 (08)
(08)
равносильный 05.
Обратим внимание. Полученное нами условие непротиворечивости представляет собой отношение двух безразмерных степенных комплексов
![]() и
и ![]() ,
,
и образует, в свою очередь, безразмерный степенной комплекс
![]() .
.
Таким образом:
● если условие непротиворечивости выполняется, то можно преобразовывать уравнение 01 в 02 и наоборот, используя масштабы.
Необходимо отметить:
● условием непротиворечивости 07 является отношением двух безразмерных степенных комплексов, образованных на базе уравнений 01 и 02;
● само условие непротиворечивости 07 представляет собой безразмерный степенной комплекс, численное значение которого равно единице.
Анализ рассуждений и рассмотренного примера показывает, что для подобия двух простых уравнений необходимо и достаточно выполнение трех условий:
● доказана сходственность этих уравнений;
● доказано, что связь сходственных переменных в уравнениях определяется масштабами;
● доказано, что масштабы оригинала и модели удовлетворяют определенному масштабному уравнению, (то есть масштабы не могут выбираться произвольно).
Понятие о степенных комплексах позволяет нам формализовать задачу оценки подобия двух уравнений.
Действительно, учитывая, что условием непротиворечивости является отношением двух безразмерных степенных комплексов, образованных на базе уравнений и масштабное уравнение представляет собой отношение двух безразмерных степенных комплексов, образованных из исходных уравнений можно поступить следующим образом:
Образуем из ранее рассмотренных сходственных уравнений 01 и 02 безразмерные степенные комплексы:
![]() (09)
(09)
![]() (10)
(10)
Условие непротиворечивости для уравнений, сформулированное выше
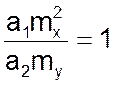 ,
,
в этом случае запишем как:
![]()
Последнее выражение служит масштабным уравнением и позволяет определить масштабы, при которых сходственные функции будут подобны.
Безразмерные степенные комплексы П1 и П2, образованные из сходственных функций, носят название «Критерии подобия сходственных функций».
Обобщим изложенное.
● Нами было рассмотрено подобие простейших объектов, имеющих простейшие математические описания в виде степенных комплексов, образованных постоянными и переменными величинами и определены условия их подобия.
● Существуют два способа получения масштабных уравнений: способ подстановки и способ получение их при помощи критериев подобия. Сущность последнего способа состоит в следующем:
■ сходственным уравнениям придается безразмерная форма;
■ определяются критерии подобия;
■ приравниванием единице отношений сходственных критериев, получают масштабные уравнения, при этом формы масштабных уравнений аналогичны формам соответствующих критериев подобия.
Можно доказать, что и в случае, когда объекты описываются уравнениями общего вида, в силе остаются все необходимые условия подобия, а масштабные уравнения можно получить теми же двумя способами.
Выше мы рассмотрели условия подобия для простых уравнений и степенных комплексов. Обратимся к ситуации, когда объекты описываются уравнениями общего вида
![]() (01)
(01)
![]() (02)
(02)
где
y1 и y2 , а также x1i и x2i неизвестные и заданные функции независимых переменных t1j и t2j
![]()
p1j и p2j - операторы дифференцирования
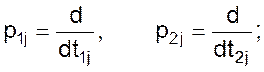
A1s и A2s – постоянные коэффициенты.
Поскольку математические описания подобны, можно утверждать, что сходственные переменные, содержащиеся в математических описаниях, связаны масштабами
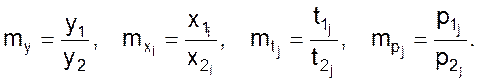 (03)
(03)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.