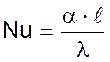
Критерий подобия Рейнольдса. Характеризует гидродинамический режим движения теплоносителя.
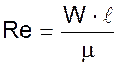
Критерий подобия Прандтля. Характеризует физические свойства теплоносителя.
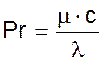
Критерий подобия Грасгофа. Характеризует режим движения теплоносителя при свободной конвекции.
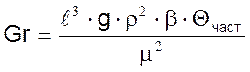
Величины, входящие в критерии, имеют следующие размерности:
■ α – коэффициент теплоотдачи, вт/(м2·град);
■ λ – теплопроводность теплоносителя, вт/(м·град);
■ μ – вязкость теплоносителя, (Н·с)/м2;
■ с – удельная теплоемкость, Дж/(кг·град);
■ ρ – плотность теплоносителя, кг/м3;
■ β – коэффициент объемного расширения теплоносителя, 1/град;
■ W – массовая скорость теплоносителя, кг/(м2·с);
■ ℓ - определяющий геометрический размер, м;
■ g – ускорение силы тяжести (9.81), м/с2;
■ θчаст. – частный температурный напор, град.
Критерии Re, Gr, Pr являются определяющими, обусловливающие тепловое подобие. Критерий Nu представляет собой определяемый (зависимый) критерий, зависящий от определяющих критериев.
Определив критерии Re, Gr, Pr, из критериального уравнения находят значение критерия Nu, а затем вычисляют коэффициент теплоотдачи из формулы
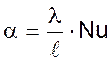
При расчете физические константы теплоносителей берутся при определяющей температуре θпл, за которую берется средняя температура теплоносителя θт, равная среднеарифметическому температур стенки θст и температуры теплоносителя θт:
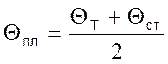 .
.
При вынужденной конвекции теплоноситель движется вдоль поверхности с определенной скоростью под действием внешней силы. В этом случае для определения α пользуются следующими уравнениями:
устойчивое турбулентное движение (Re > 10000)
![]() ;
;
переходное движение (Re = 2300…10000)
![]() ;
;
ламинарное движение (Re < 2300)
![]()
Множитель «а» в последнем уравнении имеет следующие значение:
■ для горизонтальных труб - а =0.74;
■ для вертикальных труб при движении холодного теплоносителя вверх или горячего вниз – а = 0.63;
■ для вертикальных труб при движении холодного теплоносителя вниз или горячего вверх – а = 0.85.
В приведенных уравнениях определяющим размером является внутренний диаметр трубы dв или эквивалентный диаметр канала dэкв. Определяющей температурой в двух первых уравнениях является средняя температура теплоносителя Θт,
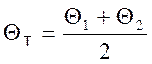
где Θ1 и Θ2 – температуры теплоносителя на входе и выходе трубки соответственно;
ΘТ – температура теплоносителя средняя, град.
а в последнем - Θпл
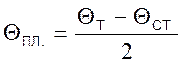
где Θст температура стенки, град.
При движении теплоносителя в кольцевом канале между двумя трубами (внутренний диаметр наружной трубы D, наружный диаметр внутренней трубы dн) коэффициент α теплообмена с поверхностью внутренней трубы определится по уравнению:
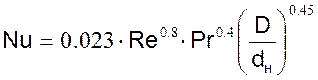 .
.
При движении в межтрубном пространстве кожухотрубных теплообменников в отсутствие поперечных перегородок
![]()
где dэкв – эквивалентный диаметр межтрубного пространства, м).
При наличии перегородок (сегментных или чередующихся дисков и колец):
![]() .
.
В последних двух уравнениях определяющим размером является наружный диаметр трубы dн, а определяющей температурой – Θт. Скорость в выражении для критерия Re, входящего в последнее уравнение, подсчитывается по приведенному сечению (см.[9]).
Для расчета α в сосудах с мешалкой пользуются уравнениями:
■ при теплообмене со стенками сосуда
![]() ;
;
■ при теплообмене со змеевиком
![]()
В этих уравнениях критерий Reм определяют по формуле
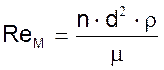
где n – число оборотов ротора мешалки в минуту, об/мин;
d – диаметр ометаемой лопастями поверхности, м;
ρ – плотность жидкости, кг/м3;
μ – вязкость жидкости, (Н·с)/м2.
При стекании жидкости по наружной поверхности горизонтальных труб, расположенных друг над другом с шагом по вертикали, равным h, коэффициент α определяется по уравнениям:
■ при 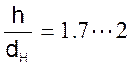
![]() ;
;
■ при 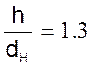
![]()
Определяющей температурой для двух предыдущих уравнений служит θТ.
При стекании жидкости по вертикальной поверхности:
■ для
турбулентного течения (Reпл. > 2300) ![]() ;
;
■ для
ламинарного течения (Reпл. < 2300) 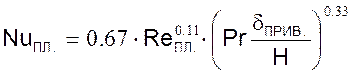
где Н – высота поверхности, м;
δПРИВ. – приведенная толщина пленки 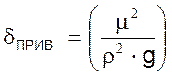
где μ – вязкость жидкости, (Н·с)/м2;
ρ – плотность жидкости, кг/м3;
g – ускорение свободного падения, 9.81 м/с2.
Определяющей температурой для двух предыдущих уравнений является θПЛ.
Критерий ReПЛ во всех критериях подсчитывается для пленки по формуле:
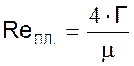 ,
,
где Г – линейная плотность орошения, кг/(м·с).[12]
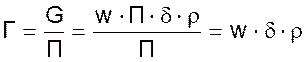
где П – периметр поверхности по которой движется пленка;
w – скорость движения пленки, м/с;
δ - толщина пленки, м;
ρ – плотность жидкости, кг/м3;
G – расход жидкости, кг/с.
Критерий Нуссельта подсчитывается по определяющему параметру δПРИВ:
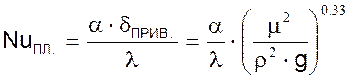 .
.
[1] Лебедев А.Н. Моделирование в научно-технических исследованиях. - М. «Радио и связь», 1989. [25]
[2] Веников В.А. Теория подобия и моделирования. М. «Высш. школа», 1976. [51]
[3] Веников В.А. Теория подобия и моделирования. М. «Высш. школа», 1976. [54]
[4] Веников В.А. Теория подобия и моделирования. М. «Высш. школа», 1976. [60]
[5] Плановский А.Н., Рамм В.М., Каган С.З. Процессы и аппараты химической технологии. М., «Химия», 1966 [148].
[6] Плановский А.Н., Рамм В.М., Каган С.З. Процессы и аппараты химической технологии. М., «Химия», 1966 [385].
[7] Плановский А.Н., Рамм В.М., Каган С.З. Процессы и аппараты химической технологии. М., «Химия», 1966 [388].
[8] Плановский А.Н., Рамм В.М., Каган С.З. Процессы и аппараты химической технологии. М., «Химия», 1966 [389].
[9] Плановский А.Н., Рамм В.М., Каган С.З. Процессы и аппараты химической технологии. М., «Химия», 1966 [444].
[10] Плановский А.Н., Рамм В.М., Каган С.З. Процессы и аппараты химической технологии. М., «Химия», 1966 [390].
[11] Плановский А.Н., Рамм В.М., Каган С.З. Процессы и аппараты химической технологии. М., «Химия», 1966 [390].
[12] Плановский А.Н., Рамм В.М., Каган С.З. Процессы и аппараты химической технологии. М., «Химия», 1966 [169].
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.