Теория подобия. Теоремы подобия. Условия осуществления подобия. Подобие уравнений общего вида, страница 3

Очевидно, что и бесконечно малые приращения (дифференциалы) также будут связаны масштабами

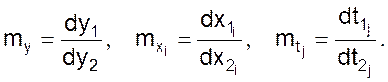                                               (04)

Обратим внимание на последний масштаб m_pj в выражении 2.3. Найдем отношение двух производных 

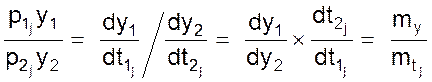                                         (05)

откуда

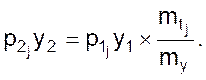                                                                         (06)              Если учесть, что

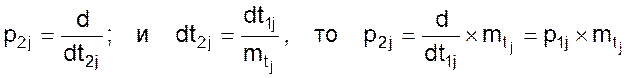             (07)

откуда

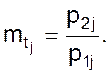                                                                                       (08)

Но полученное отношение не, что иное, как величина обратная масштабу операторов m_pj.

Тогда

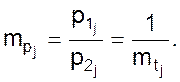                                                                             (09)

Это позволяет нам:

■  рассматривать производную p_2jy₂ как произведение двух сомножителей p_2j и y₂;

■  заменять p_2j на p_1j и y₂ на y₁ раздельно при помощи масштабов m_tj и m_y.

При таком подходе

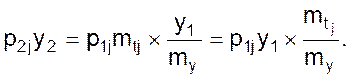                                                     (10)

Вторая производная  по тому же принципу может быть заменена сходственной переменной

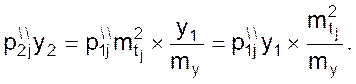                                                    (11)

Все изложенное распространяется на частные и смешанные производные.

Как и в предыдущем случае, масштабные уравнения, которые позволяют определить масштабы, можно получить двумя способами: способом подстановки и при помощи критериев подобия.

 При этом

Сущность способа подстановки состоит:

■  в замене переменных в одном из сходственных уравнений сходственными переменными второго уравнения с помощью масштабных коэффициентов;

■  в обеспечении тождественности промежуточного уравнения и второго сходственного уравнения;

■  в получении масштабных уравнений как условий тождественности промежуточного уравнения и второго сходственного уравнения.

Сущность способов критерия подобия состоит в следующем:

■  сходственным уравнениям придается безразмерная форма;

■  определяются критерии подобия;

■  масштабные уравнения получают приравниванием единице отношения сходственных критериев подобия.

3.1.  Четвертое условие подобия.

Обратившись к ситуации, когда объекты описываются уравнениями общего вида, мы предположили, что три ранее сформулированных условия подобия остаются в силе. При этом мы рассматривали случай, когда каждое из сходственных уравнений имеет единственное решение. Однако такое положение сохраняется далеко не всегда. Например, к математическим описаниям объектов, имеющим не единственное решение, помимо уравнений общего вида относятся дифференциальные уравнения, в том числе и в частных производных.

В случае если уравнение, предназначенное для описания объекта, имеет несколько решений, то ввиду того, что состояние реального физического объекта всегда однозначно, требуется указать, какое решение соответствует действительности.

Условия, конкретизирующие одно решение из нескольких, называют условиями однозначности.

Пусть математические описания представляют собой конечные уравнения и неизвестными в них являются функции y₁=y₁(t_1j)  и  y₂=y₂(t_2j). Пусть каждое из уравнений имеет два решения. При этом можно сказать, что каждое из них определяет две однозначные функции y₁₁=y₁₁(t_1j) ,  y₁₂=y₁₂(t_1j)  и y₂₁=y₂₁(t_2j)  и  y₂₂=y₂₂(t_2j) соответственно.

Пусть сходственными однозначными функциями являются y₁₁=y₁₁(t_1j) и y₂₁=y₂₁(t_2j), а также y₁₂=y₁₂(t_1j) и y₂₂=y₂₂(t_2j). В случае подобия рассматриваемых конечных уравнений  при любых значениях t_1j, t_2j, связанных масштабом

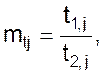                                                                                        (12)

масштаб

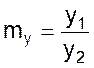                                                                                         (13)

связывает только значения сходственных однозначных функций

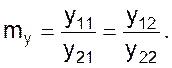
Таким образом:

■  в случае подобия объектов их однозначные состояния должны определяться сходственными однозначными функциями. Если данное условие не соблюдается, подобие объектов невозможно, несмотря на очевидное подобие сходственных уравнений;

■  в случае если математические описания объектов представляют обыкновенные дифференциальные уравнения, условиями однозначности являются начальные условия.

При этом соответствующими масштабами связываются не только t₁  и  t₂, а также y₁ и  y₂, но и производные y’₁ и  y’₂ , y’’₁ и  y’’₂, . . . , При этом должно быть

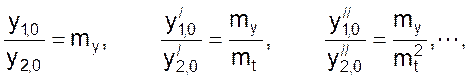                                    (14)

что означает подобие начальных условий (в данном случае условий однозначности).

Аналогично, подобие начальных условий необходимо и при описании объектов дифференциальными уравнениями в частных производных.

Таким образом, к трем условиям подобия, сформулированным выше, должно быть добавлено четвертое условие подобия  – сходственность условий однозначности решений сходственных уравнений, содержащихся у математических описаниях объектов, и пропорциональность содержащихся в них сходственных переменных.

3.2.  Пятое условие подобия.

Для подобия двух объектов описываемых функциями, имеющими неоднозначное решение,  недостаточно правильного выбора численных значений масштабов m_xi = x_1i / x_2i,  необходимо также обеспечить подобие функций независимых переменных  x_1i(t_1j), x_2i(t_2j).

Если задана функция x_1i(t_1j), то должно выполняться условие

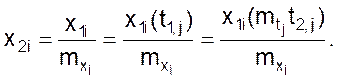                                                      (15)

Если задана функция x_2i(t_2j), то

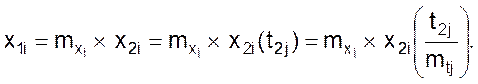                                  (16)

Из изложенного вытекает пятое условие подобия – сходственность заданных функций, содержащихся в математических описаниях объектов, и пропорциональность содержащихся в этих функциях сходственных  переменных.

Итак, для подобия двух объектов необходимо и достаточно:

1.  Иметь сходственность математических описаний;

2.  Иметь связь сходственных переменных масштабами;

3.  Иметь выбор масштабов согласно масштабным уравнениям;

4.  Иметь сходственность условий однозначности решений сходственных уравнений, содержащихся в математических описаниях объектов, и пропорциональность содержащихся в них сходственных переменных.

5.  Иметь сходственность заданных функций, содержащихся в математических описаниях объектов, и пропорциональность содержащихся в этих функциях сходственных  переменных.

4 .  Процесс подобного моделирования.

4.1.  Исходные данные, необходимые для подобного моделирования.

Для создания подобного объекта-модели необходимо располагать исходными данными, к которым относятся:

1.  Математическое описание оригинала;

                                                                  (17)