Теория подобия. Теоремы подобия. Условия осуществления подобия. Подобие уравнений общего вида, страница 4

2.  Пределы  фигурирующих  в  математическом описании  переменных величин y_o, x_oi, t_oj, если это возможно;

3.  Условия однозначности решения уравнения, описывающего оригинал;

4.  Функциональные зависимости

                                                                                    (18)

4.2.  Этапы подобного моделирования.

Процесс подобного моделирования условно можно подразделить на 8 этапов:

1.  Создаются, или выбираются из уже существующих, если это возможно, объект-модель с математическим описанием

2.  Определяются критерии подобия для оригинала Π_о и модели Π_м;

3.  Составляются масштабные уравнения;

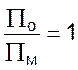                                                                                            (19)

4.  Вводятся масштабы сходственных переменных

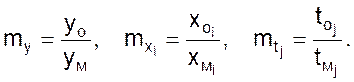                                                    (20)

и масштабным уравнениям в критериальной форме (19) придают окончательный вид;

5.  Анализируется система масштабных уравнений, при этом исключаются зависимые уравнения и устанавливается противоречивость системы масштабных уравнений, при которой если она есть подобное моделирование невозможно;

6.  Выбираются конкретные численные значения масштабов с учетом предельных значений сходственных переменных; 

7.  Определяются условия однозначности модели, подобные условиям однозначности оригинала;

8.  Рассчитываются функциональные подобные зависимости  подобные зависимостям   .

6.2.4.1.1 Пример 1.

Став обладателями атомной бомбы, американцы, в пропагандистских целях, сняли кинофильм о разрушениях, вызываемых взрывом бомбы.

Просматривая этот фильм, один американец установил, что за некоторое время t волна распространяется на расстояние R. Располагая этими данными, выполнив анализ размерностей определяющих величин, (в СИ: t - время до скачка давления, [t] = T;  R – расстояние до скачка давления в момент времени t, [R] = L; W – энергия взрыва,  [W] =L²MT^-2; r - плотность атмосферы, [r] = L^-3M) он получил критерий подобия

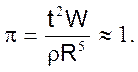                                                                                   (П1.1)

и вычислил секретную характеристику атомной бомбы: энергию взрыва W.

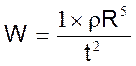                                                                                   (П1.2)

6.2.4.1.2 Пример 2.

Моделированию подлежит объект (оригинал),

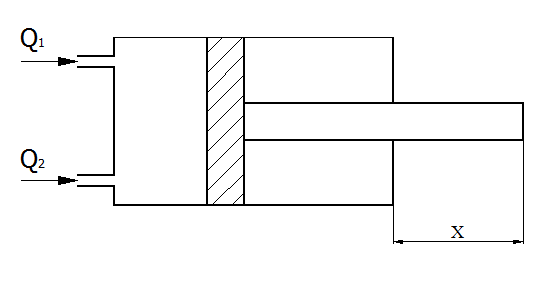
описываемый уравнением

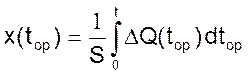,                                                                  (П2.1)

где     ΔQ – расход жидкости, м³/с;

          S – площадь поперечного сечения гидроцилиндра, м²;

          x – длина свободного конца штока гидроцилиндра, м;

          t_ор – время, с.

1. В качестве объекта-модели выбран генератор линейно изменяющегося напряжения, описываемый уравнением, сходственным с П2.1.

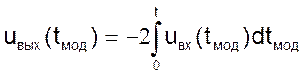                                                           (П2.2)

Введем операторы дифференцирования

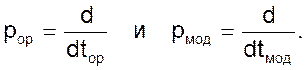
Предыдущие уравнения в операторной форме примут вид

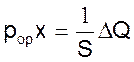                                                                                    (П2.3)

                                                                              (П2.4)

2. Приведем дифференциальные уравнения к безразмерной форме

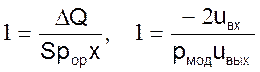
и определим критерии подобия

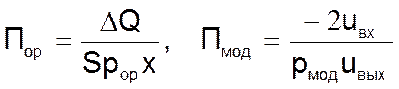
3. Масштабное уравнение в общем виде

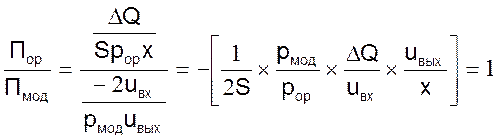                                (П2.5)

4. Введем масштабы. Для учета знака минус перед скобками сделаем следующее: в одной из пар сходственных переменных ΔQ и u_вх или  x и u_вых возьмем переменные с разными знаками

  

    

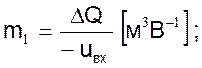
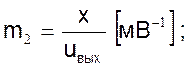
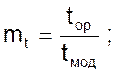
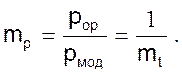
С учетом сделанных преобразований масштабное уравнение примет вид

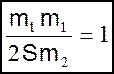                                                                                      (П2.6)

5. Полученное масштабное уравнение непротиворечиво уже в силу своей единственности.

6. Примем: S = 0.01, м²; m₁ = 4, м³В^-1; m₂ = 20, мВ^-1. Тогда m_t = 0.1. При таком масштабе процессы, протекающие в модели аналогичны по форме процессам, протекающим в оригинале, но протекают в 10 раз медленнее.

7. Нулевые начальные условия являются подобными условиями однозначности при любых масштабах.

Для расчета функции модели u₁ = u₁(t_мод), подобной заданной функции оригинала ΔQ = ΔQ(t_ор) запишем уравнение

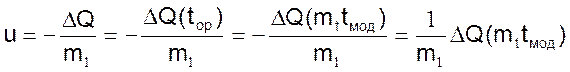                     (П2.7)

или с учетом принятых нами значений масштабов

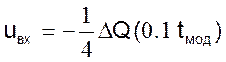
8. С учетом изложенного, если

то

5 .  Критерии подобия гидромеханических процессов[5].

Подобными, при моделировании гидромеханических процессов, считаются оригинал, и модель для которых в сходственных точках критерии подобия имеют одно и то же числовое значение.

Кинематический критерий (критерий Рейнольдса). Характеризует действие сил трения в подобных потоках и определяет режим движения жидкости (ламинарный или турбулентный). Физически представляет собой отношение сил инерции к силам трения.

.

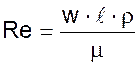Гравитационный критерий (критерий Фруда).  Характеризует действие сил тяжести в подобных потоках и физически представляет собой отношение сил инерции к силам тяжести.

.

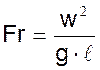Критерий гидравлического сопротивления (критерий Эйлера). Характеризует действие сил давления в подобных потоках и физически представляет собой отношение сил давления в потоке к силам инерции.

.

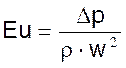Физические величины, которые входят в формулы критериев:

■  w – средняя скорость движения жидкости, м/с;

■  ℓ - основной (определяющий) линейный размер канала ( для трубы ее диаметр) по которому движется жидкость, м;

■  Δр – потеря давления, Н/м²;

■  ρ – плотность жидкости, кг/м³;

■  μ – вязкость жидкости, (Н·с)/м².

Критерии Re и  Fr составлены из величин, определяющих распределение скоростей в потоке (w, ℓ, ρ, μ), и поэтому являются основными (определяющими) критериями гидравлического подобия. Если эти критерии для оригинала и модели равны, то существует одинаковое соотношение между действующими в потоках силами. При равенстве критериев Re и Fr для оригинала и модели равенство критериев Eu получается само собой, так как перепад давления является следствием распределения скоростей в потоке.  

6 .  Критерии подобия для тепловых процессов.

6.1.   Передача тепла конвекцией[6].

Тепловое подобие заключается в том, что температуры в отдельных точках трубы подобны, т. е. отношение разности температур между двумя любыми точками одной трубы к разности температур между сходственными точками другой трубы является постоянной величиной.

Процесс передачи тепла конвекцией определяется рядом критериев подобия (критерии размерности не имеют):

Критерий подобия Нуссельта. Характеризует процесс теплообмена между теплоносителем и стенкой.