Файл Модели\САМРаботы02\САМ07а.doc 2 стр. 122 Кбайт
Раздел.
1. Программирование уравнений, содержащих производные в правой части.
В инженерной практике встречаются дифференциальные уравнения,
правая часть которых является линейной комбинацией вида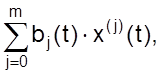 
где
bj(t) – заданные
переменные или постоянные коэффициенты, а x(j)(t) – производная j–го порядка по аргументу t от
заданной функции x(t). Примером
может служить следующая задача:
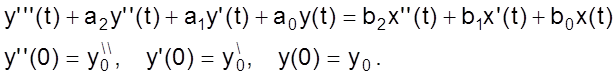(01)
Чтобы решить данное уравнение общим методом необходимо воспроизводить производные функции x(t) в правой части уравнения.
В ряде случаев, для уравнений, которые можно записать в виде суммы полных производных различных порядков (последнему требованию удовлетворяют линейные дифференциальные уравнения и даже некоторые нелинейные), можно избежать воспроизведения производных x(t), сведя дифференциальное уравнение к эквивалентным системам дифференциальных уравнений, не содержащих производных функции x(t).
В качестве примера получим решение уравнения 01.
Для начала представим его в виде суммы полных производных
(02)
Теперь последовательно дважды проинтегрируем полученное выражение. После первого интегрирования получим
(03)
где z1(t)
получено интегрированием из 
После второго интегрирования получим
(04)
где z2(t)
получено интегрированием из 
В результате получим систему дифференциальных уравнений вида:
(05)
С начальными условиями
Очевидно, что система уравнений 5 не содержит производных от функции x(t) поэтому функция x(t) может иметь достаточно произвольный вид и даже разрывы первого рода. Полученную систему уравнений 5 принято называть канонической формой уравнения 1.
В среде SIMULINK структурная схема решения будет иметь вид
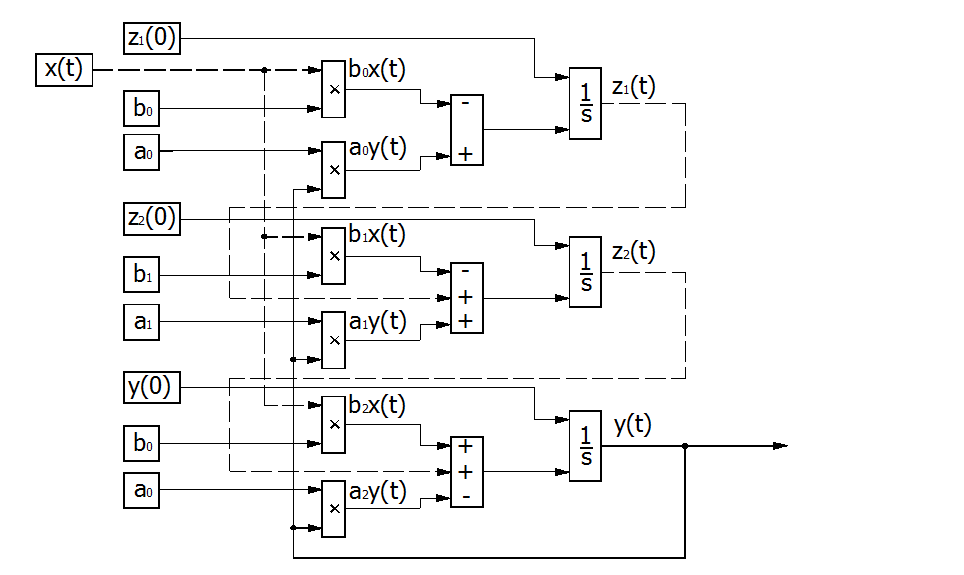
Рис.1. Структурная схема решения дифференциального уравнения в элементах SIMULINK.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
