Программирование уравнений, не разрешенных относительно старшей производной

Файл САМРаботы01\САМ04а.doc          2 стр.            100 КБ

1. Программирование уравнений, не разрешенных относительно старшей производной.

Иногда приходится искать решение дифференциальных уравнений, которые не могут быть разрешены относительно старшей производной.

Например, дана задача Коши n-го порядка

где  и соответственно

в которой дифференциальное уравнение не разрешено относительно старшей производной.

В этом случае для решения задачи можно воспользоваться методом неявных функций. Суть метода состоит в том, что от задачи Коши n-го порядка переходят к задаче Коши n + 1 порядка, в которой дифференциальное уравнение разрешено относительно новой старшей производной.

                  (01)  

где K – коэффициент (достаточно большое число);

производная  предполагается отличной от нуля.

Знак производной вводится в уравнение для того, чтобы всегда имела место отрицательная обратная связь, так как  только в этом случае можно получить устойчивое решение уравнения.

Поскольку последнее уравнение разрешено относительно старшей производной, к нему применим общий метод решения дифференциального уравнения.

Пример 5.

В качестве примера используем задачу отыскания по заданной функции x(t) другой функции m(t), которая определяется выражением

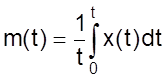                                                                                (02) 

и носит название: «Текущее среднее».

Для воспроизведения m(t) реализуем уравнение первого порядка, не разрешенное относительно производной

                                                                      (03)

Чтобы записать его в виде 01, определим знак частной производной

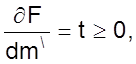
Тогда дифференциальное уравнение примет вид

                 (04)

Решение последнего уравнения средствами SIMULINK может иметь вид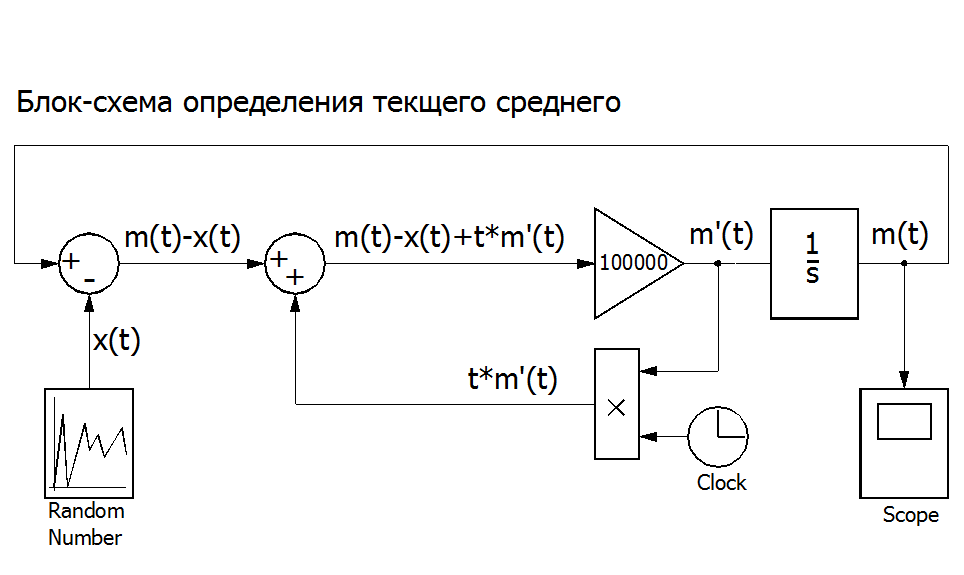

   Рис. П5.1. Блок-схема решения дифференциального уравнения[1].

---