Регулятор давления ПР-1.5, страница 7

          Из рисунка  5  видно ,  что  график не  охватывает  точку  с  координатами  (-1  , j , 0 ) , следовательно система устойчива и в замкнутом состоянии .

[ 9 cтр. 206-230, 258-260].

4  ПОСТРОЕНИЕ И АНАЛИЗ ЛАЧХ НЕИЗМЕНЯЕМОЙ ЧАСТИ СИСТЕМЫ

          4.1 Построение ЛАЧХ неизменяемой части системы

Микропроцессор является машиной дискретного действия , которая выдает результаты через установленные периоды повторения , а в промежутках между выдачей команд выход от микропроцессора сохраняет свое значение постоянным .Поэтому для расчетного исследования дискретной микропроцессорной системы используется  z –преобразование .Дискретность микропроцессора серии К-588 равна десяти .

На вход исследуемой системы подается ступенчатая функция на протяжении всего периода повторения . Найдем передаточную функцию разомкнутой дискретной системы с микропроцессором .

Определим изображение входной величины :

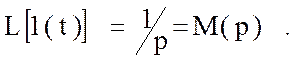                                                                        ( 56 )

Определим изображение выходной величины :

                                                                ( 57 )

          Передаточная функция разомкнутой системы :

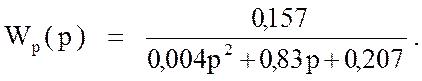                                                              ( 58 )

          Тогда , разделив все члены выражения (58 ) на свободный член 0,207 получим выражение вида :

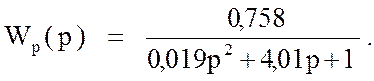                                                                    ( 59 )

          Приведем выражение ( 59 ) к стандартному виду :

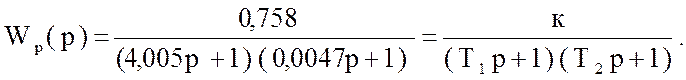                         ( 60 )

          Запишем  z-преобразование для дискретной функции :

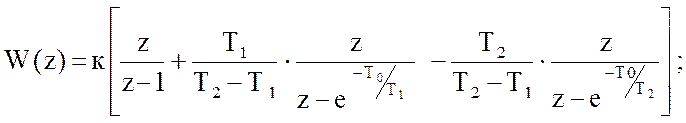                         ( 61 )

           где   Т о – период дискретной функции .

          Для получения переходной функции разомкнутой дискретной системы с запоминанием следует z-преобразование переходной характеристики непрерывной части умножить на 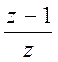 ( фиксатор нулевого порядка ) :

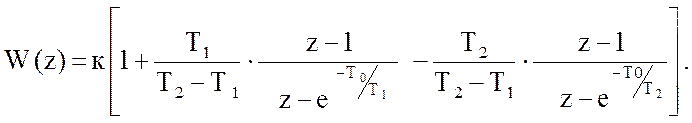                        ( 62 )

          Для использования в расчете метода логарифмических частотных характеристик , необходимо перейти к псевдочастоте . Для этого осуществим w – преобразование :

                                                                                                    ( 63 )

            =

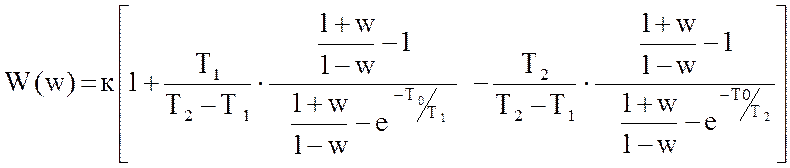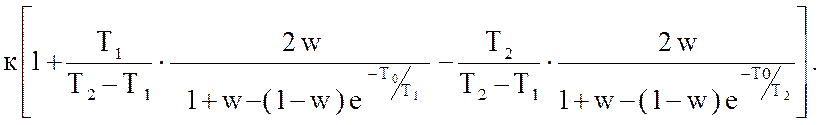          (64)

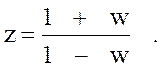
          Перейдем от w – изображения к частотному выражению передаточной функции  . Для этого применяем подстановку :

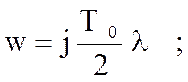                                                                                                  ( 65 )

          где      -  псевдочастота , мин ^–1 .

Тогда передаточная функция от псевдочастоты имеет вид : 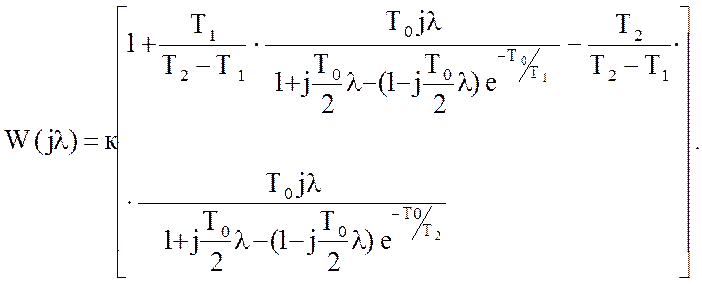                             ( 66 )

          Из условия занятости вычислительной машины период дискретности Т0= 10 с. = 0,166 минут .

          Тогда при подстановке числовых значений в формулу (66 ) получим выражение :

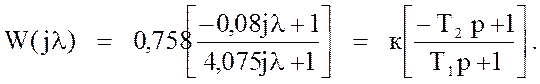                                                ( 67 )

          Таким образом получили выражение комплексной частотной характеристики , на основании которой строится ЛАЧХ . Асимптотическая ЛАЧХ представляет собой ломанную линию , имеющую точки излома в сопрягаемых частотах , определяемых постоянными времени звеньев .

          Частоты сопряжения :

          2 = 1/0,08  =  12,5   .                                                                             ( 68 ) 

          1 = ¼,075 =  0,24   .                                                                               ( 69 )

          Для построения логарифмической амплитудной характеристики найдем 20 lg / W ( j  ) / .

          20 lg / W ( j  ) /=20lg 0,758 + 20lg /(1-0,08jw)/ -20lg/(1+4,075 j)/ . (70)

          В формуле (67) выражение вида ( 1+Тр ) , стоящее в числителе , соответствует увеличению наклона ломанной на 20дб/дек , а в знаменателе – уменьшение на 20дб/дек .

          Построение  ЛАЧХ начинается с проведения горизонтальной линии на высоте 20lg к , где к = 0,758 . Эта линия проводится до пересечения с асимптотой проходящей  через l1  перпендикулярно оси  lg l . В точке пересечения происходит преломление ЛАЧХ на величину – 20дб/дек . При пересечении прямой с асимптотой , проведенной через l2 снова происходит излом и наклон кривой увеличивается на 20дб/дек . Полученная ломанная соответствует ЛАЧХ неизменяемой части , которая показана на рисунке  6 .

4.2  Анализ ЛАЧХ неизменяемой части

Из формулы (67) передаточной функции проанализируем форсирующее звено с запаздыванием ( из-за наличия знака минус ) и апериодическое звено первого порядка .

На графике ( рисунок 6 ) проведем вертикальные прямые через сопрягающие частоты . Для частот , меньших l1 = 0,24 выражение записывается в виде :

L (jl)= 20 lg к .                                                                                   (71)

Выражению вида (71) соответствует прямая линия , параллельная оси частоты , иначе колебания низких частот пропускаются величиной , равной коэффициенту передачи звена к .

Для частот , больших l1 выражение можно записать в виде :

L (jl)= 20 lg 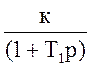   .                                                                      (72)

Выражению (72) соответствует прямая с отрицательным наклоном 20дб/дек .

Рассмотрим форсирующее звено с запаздыванием . Асимптотическая ЛАЧХ представлена в виде двух прямых . Одна прямая с нулевым наклоном при l2 < 1/Т2 , а другая прямая  имеет  положительный  наклон   20дб/дек   при

l2 >1/Т2 . При l2 >1/Т2 происходит компенсация двух звеньев : - 20дб/дек апериодического звена и 20дб/дек форсирующего звена  . В итоге при сопрягающей частоте l2 получаем прямую с нулевым наклоном .

[ 8  стр.110-122 ], [ 9  стр. 162-190].

          5 ПОСТРОЕНИЕ И АНАЛИЗ ЖЕЛАЕМОЙ  ЛАЧХ

          Все методы построения желаемой ЛАЧХ ( построение желаемой ЛАЧХ по В.В. Солодовникову , по Е.А. Санковскому – Г.Г. Сигалову ) содержат некоторые допущения , кроме того графические этапы расчета вносят неизбежные неточности .Поэтому расчет чаще всего дает лишь приближенные значения необходимых параметров .Однако они легко уточняются при испытании макета САР . Учитывая эти обстоятельства я использую упрощенный метод построения желаемой ЛАЧХ .