Регулятор давления ПР-1.5, страница 2

-  номинальная мощность Nе , кВт ----------------------------------------    56 ;

-  частота вращения коленчатого вала при

     номинальной мощности nN об/мин-------------------------------------  5600 ;

-   число цилиндров , i  ------------------------------------------------------------ 4 ; 

-  максимальный крутящий момент Ме макс , Н*м (кГ*м) ---105,9 (10,8) ;

-  инерционность двигателя ,мс  ----------------------------------------  до 20   ;

-  частота вращения коленчатого вала

     при макс. крутящем моменте  n м  , об/мин  --------------------------- 3500 ;

-  минимальный удельный расход топлива  g е мин. , г/кВт * ч ----- 307   ;

-  плотность топлива , р т , г/cм ²  ----------------------------------------- 0,542 ;

-  коэффициент самовыравнивания двигателя , к д  -------------------  0,07 ;

-    тактность двигателя  , t ---------------------------------------------------      4 .

2.1.2      Расчет передаточной функции ДВС

Установившийся режим работы двигателя, (постоянство угловой скорости ) ,  поддерживается при выполнении условия  :

                                                                                      ( 1 )

    где    Ме –момент сопротивления потребителя энергии (Н·м) ;

    Мс – крутящий момент (Н·м).

Режим работы двигателя характеризуется совокупностью параметров (в ряде случаев их средним значением за цикл ) обуславливающих его эффективную работу . К числу таких параметров можно отнести крутящий момент М е , угловую скорость коленчатого вала w , цикловую подачу топлива g ц , и ряд других ) . Совокупность этих и других параметров может быть  выражена обобщенными функциональными зависимостями  вида :

                                                      (2 )

Режим работы двигателя установившийся , при котором параметры входящие в зависимость  ( 2 ) с течением времени не изменяются . ( Для некоторых из этих параметров , например для М е и w ,  понятие постоянства во времени относится к их среднему значению за цикл работы .)

          Нарушение установившегося режима может произойти вследствие изменения моментов М е или М с . Уравнение динамического равновесия при этом имеет вид :

I dw/dt = (М е + Δ М е ) – ( М с + Δ М с ) ;                                             ( 3 )

          где          I – приведенный к валу момент инерции двигателя

          и связанных с   ним агрегатов потребителя ( мм/сек);

          Δ М е  и Δ М с – приращения соответствующих моментов ( Н·м) .

C учетом равенства ( 1 )  :

           I dw/dt  = Δ М е – Δ М с  .                                                                    ( 4 )

Момент сопротивления Мс потребителя зависит от скоростного режима и нагрузки ( настройки потребителя) , определяемой обобщенной координатой N . Следовательно  , М с = f (w ; N ) . При разложении полученной зависимости в ряд и линеаризации получаем :

.                                                 ( 5 )

          Крутящий момент  М е двигателя зависит от скоростного режима  w  , и цикловых подач топлива . В свою очередь цикловая подача топлива определяется положением « h » органа управления , и угловой скоростью коленчатого вала  w  . Следовательно :   М е = f (w ; h ) . После разложения в ряд Тейлора и линеаризации получаем :

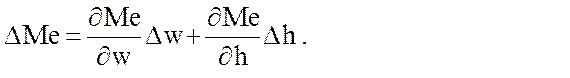                                        (6 )

          Для оценки устойчивости режима работы двигателя может быть использовано отношение :

           Fд = ∆ ( ∆ М ) / ∆ w = ( ∆ М с - ∆ М е ) /∆ w   ;                                    ( 7 )

           где      F д  - фактор устойчивости двигателя .   

Приращение момента  ∆ М е  при изменении угловой скорости  на ∆ w может быть найдено путем разложения функции  М е = f ( w )   в ряд Тейлора . После замены dw на конечное малое приращение ∆ w  :

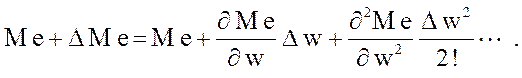                                               ( 8 ) 

Если отклонение  ∆ w от равновесного значения мало , то членами разложения в ряд Тейлора со второй и более высокими степенями ∆ w можно пренебречь , и тогда ∆ М е = (дМ е / д w ) ∆w  и аналогично :

           ∆ М с = (дМ с / дw ) ∆w  .                                                                   ( 9 )

После подстановки выражения ( 7 ) в ( 9 )  получим формулу ( 10 ) :

           F д = дМ с / дw – дМ е / дw   .                                                            (10 )

Подстановка выражений ( 5 )  и ( 6 ) в исходное уравнение ( 4 ) позволяет с учетом формулы ( 10 ) получить дифференциальное уравнение собственно двигателя  в виде :

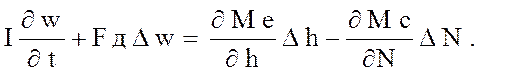                                              (11) 

Если в полученное уравнение ввести относительные величины отклонений параметров от их значений на равновесном режиме ( угловой скорости w₀ коленчатого вала , положения h ₀ органа управления и настройки потребителя N₀  ) в виде отношений -   ;   ; и разделить все члены уравнения на коэффициент при  , то уравнение ( 11 ) примет вид :

          Т_д dφ / dt + к_дφ = η – θ _д  a _д .                                                             ( 12 )

В этом уравнении время двигателя  Т_д =  I w₀ / ( q _{м h} h ₀ ) – характеризует инерционность двигателя как регулируемого объекта и не должно превышать 20 мс .

          Коэффициент самовыравнивания  к_д  = F_д w₀ / ( q _{м h} · h ₀)  -  характеризует   устойчивость    режимов     работы    двигателя  .   Принимаем

к_д =0,07.

          Дифференциальное уравнение можно записать в операторной форме . Уравнение ( 12 ) в операторной форме примет вид :

d (p)j = h - q _д · a _д   ;                                                                         ( 13 )  где     d( p)  -  собственный оператор собственно двигателя .

           a ( р ) = Т_д р + к _д .                                                                                  ( 14 )

Левая часть дифференциального уравнения ( 13 ) определяет собственные динамические свойства двигателя , а в правой части сосредоточены члены , определяющие возмущающие воздействия на двигатель .