Регулятор давления ПР-1.5, страница 5

          W _{( p )}   = U _макс / a _макс  = 3 / 700  = 0,0043 .                                       ( 38 )

[ 5 стр. 17-20 ] .

2.6  Выбор датчиков теплового состояния двигателя и окружающего воздуха , и определение их передаточной функции

          В качестве датчиков теплового состояния двигателя и окружающего его воздуха  я выбираю термопреобразователи с унифицированным токовым сигналом марки ТСПУ – 9313 .

          Термопреобразователь ТСПУ – 9313 применяется для измерения температуры жидких и газообразных сред .

          Технические характеристики :

      -   показатель тепловой инерции , с.  --------------------   не более –3 ;

      -   выходной сигнал   ---------------  4-20 мА, 0-5 мА , 0-5 В , 0-10 В ;

      -   напряжение питания , В   ------------------------------------  12 ¸ 42   ;

      -   потребляемая мощность , Вт  --------------------------  не более 0,9 ;

      -   зависимость выходного сигнала от измеряемой

           температуры   ------------------------------------------------- линейная ;

      -   схема включения  ------------------------------------- двухпроводная ;

      -   покрытие   -----------------------------------------    антикоррозийное ;

      -   длина , l  ( мм )  --------------------------------------------------------100 .   

Передаточная функция   –    линейная зависимость выходного  сигнала ( мА ) от оптимальной температуры .  Оптимальная  температура двигателя –30 ^оС .

Передаточная функция имеет вид :

 W _{(  p )}     =   5 / 30   =   0,17   .                                                             ( 39 )         

3 ПЕРЕДАТОЧНАЯ ФУНКЦИЯ НЕИЗМЕНЯЕМОЙ ЧАСТИ  СИСТЕМЫ. ОЦЕНКА УСТОЙЧИВОСТИ СИСТЕМЫ

На основании того , что определены передаточные функции элементов системы , я строю структурную схему системы . Структурная схема системы автоматического регулирования расхода топлива в двигателе показана на рисунке 2 .

К неизменяемой части относятся элементы , которые присутствуют для обеспечения работоспособности системы , а именно двигатель , топливоподающий электронасос , датчики соответственно расхода , ускорения , частоты и температуры . Изменяемой частью системы является микропроцессор .

Передаточная функция неизменяемой части системы имеет вид :

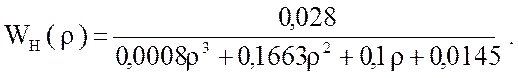                                      ( 41 )

Устойчивость системы автоматического регулирования расхода топлива можно достаточно легко исследовать путем введения типовых трапецеидальных частотных характеристик . При этом необходимо заменить  в передаточной функции р  на jw и разделить передаточную функцию на действительную и мнимую части . После необходимых преобразований формула  ( 40 ) принимает вид :

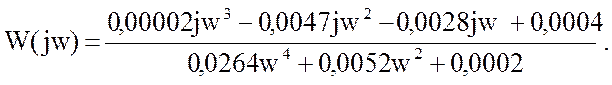                        ( 42 )

Действительная часть :

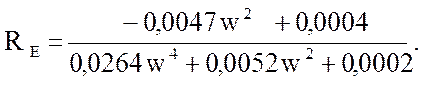                                                   ( 43 )

Мнимая часть :

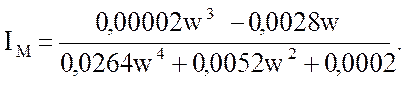                                                      ( 44 )

 Для построения переходного процесса методом трапеций запишем действительную частотную характеристику системы :

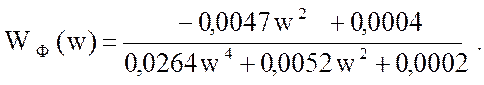                                                    ( 45 )

Построим зависимость  от изменяющейся частоты wпо таблице 1.

           Таблица 1 . Зависимость  от частоты  w .

w	WФ( w )	w	WФ( w )	w	WФ( w )	w	WФ( w )
0	2	0,4	-0,2	1	-0,135	100	-0,00002
0,2	0,47	0,5	-0,25	2	-0,04	¥	0

          Зависимость  действительной частотной характеристики   от изменения частоты w показана на рисунке 3 .

          При замене действительной вещественной частотной характеристики  прямолинейными отрезками всю площадь , заключенную между осями координат и частотной характеристикой я разбиваю на ряд трапеций : авс , свde , lfmn ,  mnkи .

Трапеция  авс : U _{Ф 01} = 1,53                    Трапеция свde: U _{Ф 02} = 0,67               

                              w _d1 = 0                                                       w _d2 = 0,2

                              w ₀₁ = 0,2                                                    w ₀₂ = 0,4

                              c ₁  = 0                                                         c ₂  = 0

Трапеция lfmn : U _{Ф 03} = -0,115                    Трапецияmnkи: U _{Ф 04} = -0,04                

                              w _d3 = 0,5                                                        w _d4 = 1

                              w ₀₃ = 1                                                           w ₀₄ = 2

                               c ₃ = 0,5                                                          c ₄ = 0,5

          В таблице 2 рассчитаны значения ординат х _n переходных процессов для единичных трапецеидальных действительных частотных характеристик при разных значениях времени t_{n ,}при определенных для каждой из трапеций значениях  c .

           х _n = U _{Ф o  n}   · h (x _n ) .                                                                           ( 46 ) 

           t = t / w _{o n} .                                                                                            ( 47 )                     

          На рисунке 4 построен график переходного процесса рассчитанного в таблице 2 . Из графика 4 определим качество процесса регулирования .

Время регулирования  t _рег  равно 25 секунд .

          Перерегулирование :

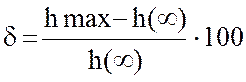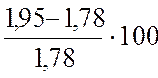         % =  % = 9,55 % .                          ( 48 )

          Устойчивость режимов работы системы автоматического регулирования расхода топлива в двигателе определяется характером его переходных процессов и следовательно алгебраическим знаком корней характеристического уравнения . Однако часто порядок дифференциального уравнения двигателя оказывается достаточно высоким , в связи с чем определение корней характеристического уравнения является задачей достаточно трудоемкой . Чтобы избежать трудностей при оценке устойчивости работы системы воспользуемся критерием Рауса-Гурвица .