Логарифмические эквивалентные амплитудные и
фазовые характеристики сложных нелинейных элементов
Для подавления автоколебаний или распределения областей устойчивых состояний в некоторых типах нелинейных систем применяют сложные нелинейные элементы, представляющие собой сумму параллельно нелинейных или последовательных соединений нелинейностей, разъединенных линейным звеном и линейных элементов, образующих внутренние контуры с отрицательной и положительно обратной связью.
 |
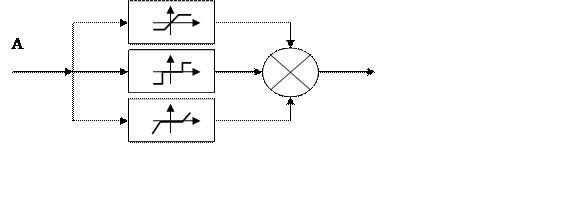Рисунок 31
Для получения логарифмических и фазовых характеристик сложных нелинейных характеристик используются шаблоны характеристик каждого элемента, по которым строится суммарная характеристика.
 |
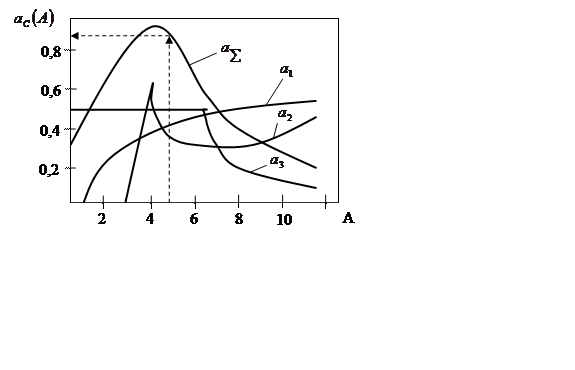Рисунок 32
Статическая линеаризация существенных
дискретных нелинейных элементов
Квантование по времени в ЛСА осуществляется импульсными устройствами на основе трех типов модуляции: АИМ, ШИМ, ЧИМ. Быстродействующие устройства с АИМ являются линейными импульсными элементами, а устройства с ШИМ и ЧИМ – нелинейными.
Нелинейный импульсный элемент для удобства математического описания можно представить в виде совокупности линейного и нелинейного элемента. Сигнал на выходе с двухзначного нелинейного элемента записывается в виде:
,
(126)
где
.
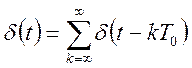(127)
При этом будем считать, что входной сигнал является гармоническим, то есть
, (128)
где
;
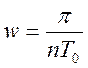(129)
- полупериод
гармонического колебания, (
).
.
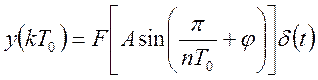(130)
При учете первой гармоники, выходной сигнал будет равен:
,
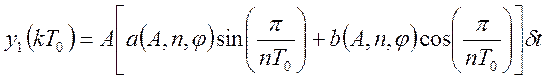(131)
Определим условие наилучшего квадратичного приближения
к 
для
этого запишем соотношение:
,
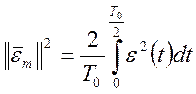(132)
где
- полупериод функции 
.
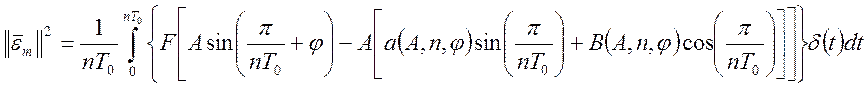. (133)
После преобразования получим
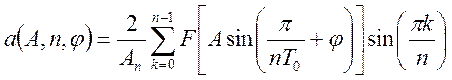, (134)
.
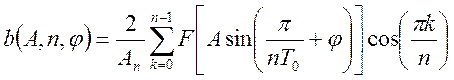(135)
Пользуясь этими двумя формулами, найдем эквивалентную передаточную функцию.
,
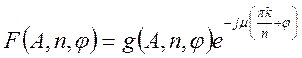(136)
где
,
(137)
.
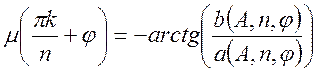(138)
Вычислительные процедуры для определения коэффициента гармонической и статической линеаризации нелинейных элементов
Для сложных видов дискретных нелинейностей довольно трудно получить формулы, позволяющие вычислить коэффициент гармонической и статической линеаризации. В этом случае можно рекомендовать пользоваться программами, составленными на языке ПЛ/1 для различных численных процедур интегрирования. Так, например, программа TRP, предназначенная для вычисления коэффициентов в гармонической неоднозначной нечетно-симметричной нелинейности методом трапеции.
Математическая модель САР
Большинство ЛСА можно привести к двум структурам, упрощенная схема которых:
 |
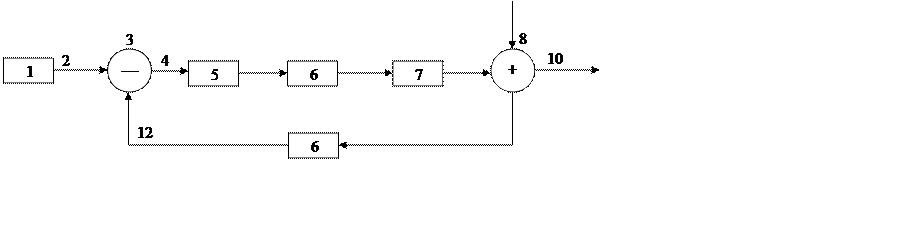а)
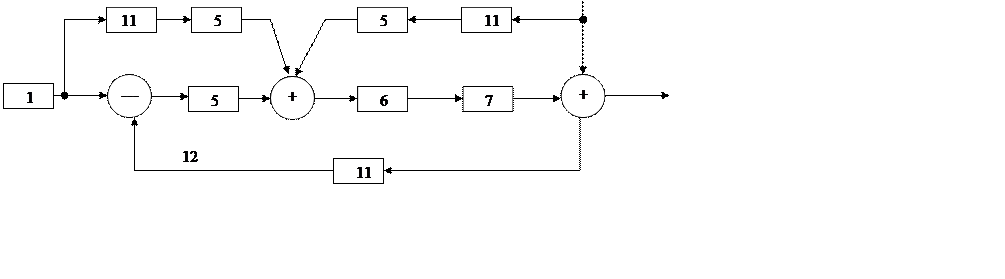б)
Рисунок 33
На этих схемах управляющий сигнал 2 формируется в задающем устройстве. Он сравнивается в устройстве 3 с выходными сигналами, который измеряется датчиком параллельно. В результате сравнения сигналов образуется сигнал разноси4, поступающий через устройство управления 5 и 6 на объект регулирования 7. От действия сигнала возмущения 8, поступающего в систему через сумматор 9 происходит некоторое искажение выходного сигнала 10. Замыкание системы осуществляется с помощью главной ОС 12. Если в этих рисунках исключить задатчик, то получим систему автоматической стабилизации, обрабатывающий сигнал возмущения.
Рисунок 33 б) от а) отличается тем, что в нем для получения более высокой точности применения три датчика параллельно. Которые не только измеряют выходной сигнал 10, но и сигнал управления 2 и возмущения 8. Эти два сигнала после прохождения устройства 5, поступают на сумматор 13 и уменьшают влияние синтеза и анализа на ошибку ЛСА. Практически все ЛСА при решении задач синтеза и анализа сводится к этим двум схемам. При этом пользуются правилами преобразования структурных схем, выделяют линейную, нелинейную и цифровую части.
Наряду с передаточными функциями линейных элементов используются эквивалентная передаточная функция нелинейных элементов. Для однозначных нелинейностей они совпадают с коэффициентами гармонической линеаризации.
Если система имеет сигналы на выходах и входах в векторной форме, то в ЛСА несколько входных исполнительных и корректирующих устройств.
В векторно-матричном уравнении, описываемом ЛСА, по своему описанию ничем не отличается от соответствующих уравнений объектов. Только в них входные расширенные матрицы, в которых учитывается уравнениями корректирующих и исполнительных устройств.
Так как в современных ЛСА входные управляющие ЭВМ. При необходимом для реализации численных процедур любой дискретной модели.
Для определения дискретных моделей необходимо пользоваться предварительной реализацией на ЭВМ специальные программы.
Управляемость и наблюдаемость
Позволяет оценить правильность выполнения структурных преобразований, при этом следует иметь в виду, что управляющие сигналы должны переводить системы из любого начального состояния в установившемся за конечное время – это управляемость и по выходному сигналу однозначно определить начальное состояние системы – это наблюдаемость.
Процессы называются управляемыми, если на каждую переменную состояния можно целесообразно воздействовать с помощью сигнала взаимодействия, в течение конечного действия.
Если переменное состояние не зависит от управления, то отсутствует возможность требуемого ее изменения во времени, и она является не управляемой.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.