Понятие локальных систем автоматики. Общие подходы к проектированию, страница 2

Пример № 2. Уравнение вертикально стартующей вверх ракеты род действием силы тяги двигателя.

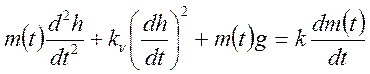                                            ,                                 (15)

- уравнение не линейное и не стационарное.

где    - высота подъема,

 - коэффициент пропорциональности,

 - коэффициент трения,

 - ускорение свободного падения.

Ведем следующие обозначения:

                                                                ,                                                        (16)

                                                                .                                                        (17)

                                            

                                                      .

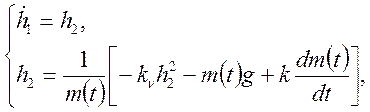
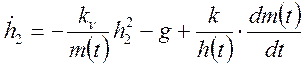При описании элементов дискретного действия в общем виде используют уравнения:

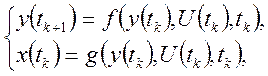                                                                                            (18)

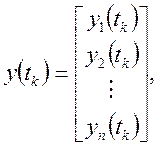
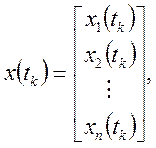
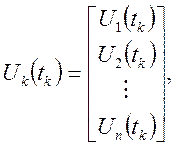                                                   (19,20,21)

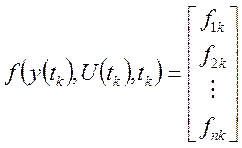                                             ,                                                  (22)

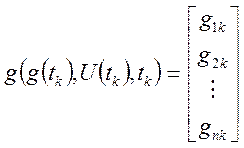                                             .                                                  (23)

Наиболее распространенным случаем, является случай, когда такт квантования равен постоянному времени .

Тогда уравнение (18) запишется в виде:

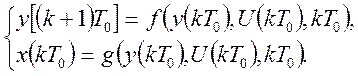                                                                               (24)

Составим разностное уравнение для численных процедур интегрирования и их реакции на управляющей ЭВМ.

Пусть

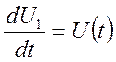                                                             .                                                    (25)

Начальные условия:

                                                                  ,                                                  (26)

                                                                  .                                                  (27)

Для метода Тейлора:

                                                             .                                          (28)

Для метода Адаме-Башворта:

                                                           .                                       (29)

Для метода Адамс-Мультон:

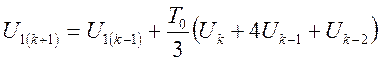                                           ,                                (30)

Уравнения (28), (29) и (30) реализуются в виде рабочих программ на управляющей ЭВМ.

Методы линеаризации уравнений

Дифференциальные уравнения можно линеаризовать следующими методами:

1. нелинейная функция рабочей области раскладывается в ряд Тейлора.

2. Заданные в виде графов нелинейные функции линеаризуются в рабочей плоскости прямыми.

3. Вместо непосредственного определения частных производных, вводятся переменные в исходные нелинейные уравнения.

                                                     ,                                                           (31)

                                                    ,                                                             (32)

                                                     .                                                         (33)

4. Данный метод основан на определении коэффициентов по методу наименьших квадратов.

Пример: Пневмопривод с встроенной трубкой.

 

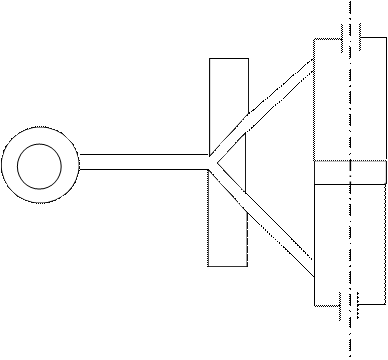
Рисунок 6

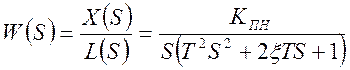,                                                                               (34)

где    - постоянное времени пневмопривода;

  - передаточный коэффициент пневмопривода;

 - коэффициент демпфирования пневмопривода.

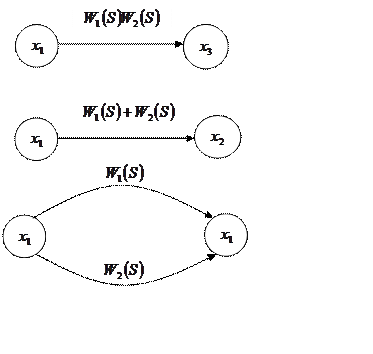
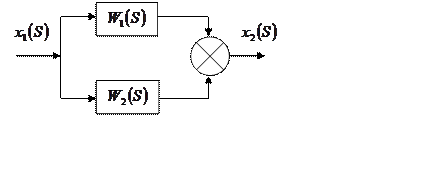
Внутреннее строение элементов САР наиболее просто определяется с помощью структурных схем графов. В отличие от известных структурных схем в графах, переменные указываются в виде времени, а дуги обозначают или параметры, или передаточные функции типовых звеньев. Между ними существует четное соотношение.

 

 

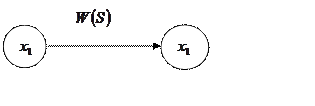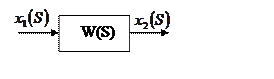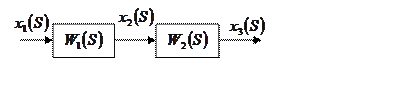Рисунок 7

Существует 49 звеньев в таблице с амплитудными, фазовыми и амплитудно-фазовыми характеристиками. Типовых звеньев и 49 типовых звеньев с ЛАЧХ и ЛФЧХ.

Пример № 1.

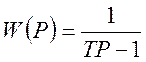.                                                                                                             (35)

 

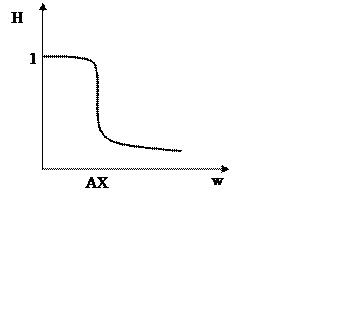Рисунок 8 – Амплитудная характеристика

 

Рисунок 9 – Фазовая характеристика

 

Рисунок 10 – Амплитудно-фазовая характеристика

Пример № 2.

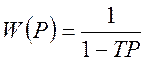.                                                                                                             (36)

 

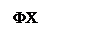Рисунок 11 – Амплитудная характеристика

 

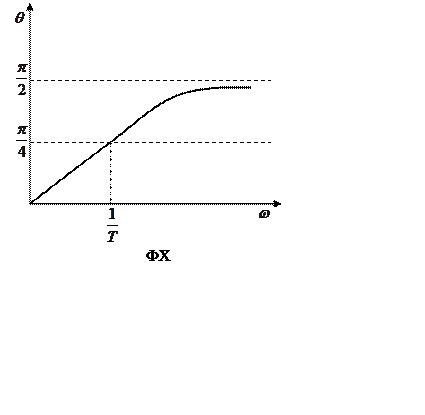Рисунок 12 – Фазовая характеристика 

 

Рисунок 13 – Амплитудно-фазовая характеристика

Существует таблица поправок логарифмическим характеристикам, монограмма замыкания, используется регрессивный анализ для получения математической модели ОУ. Дается монограмма № 1 , предназначенная для вычисления коэффициентов регрессивной модели. При проектировании непрерывных, дискретно-непрерывных и дискретных САР, надо знать статическое моделирование ОУ.

Дискретная система, передаточная функция, частотные характеристики, импульсные переходные функции, удобно лишь при моделировании. При высоких порядках математического моделирования модели также процедуры требуют использования значительных временных затрат. Именно поэтому стали пользоваться векторно-матричными формами записи данных уравнениями. При этом один линейный объект входит две матрицы А и В.

Стационарный объект можно записать в виде векторно-матричного уравнения:

,                                                                                                        (37)

,                                                                                                  (38)

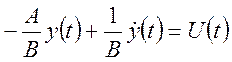 - нормальная форма записи.                                                 (39)

где     и  - векторы размерности  и .