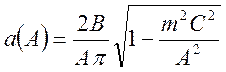 ,
(95)
,
(95)
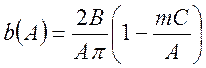 ,
(96)
,
(96)
![]() .
.
С помощью шаблонов находят амплитуды и частоты автоколебаний в нелинейных системах и строим области устойчивых и неустойчивых состояний по параметрам линейной и нелинейной части.
Существует два типа двухзначных нелинейностей: пассивные и активные.
Под пассивными – понимается такие двузначные нелинейности, которые за один период входного сигнала нелинейная характеристика обходится против часовой стрелки. В этом случае в выходном сигнале наблюдается фазовое запаздывание. Если обход нелинейной характеристики проходит по часовой стрелке, то двузначная нелинейность является активной и в выходном сигнале имеет место фазовое опережение. Активные нелинейности применяют в устройствах коррекции СА для обеспечения устойчивости. Реализация таких устройств может быть выполнена на электронных элементах или в виде рабочей программы.
Рассмотрим гармоническую линеаризацию нелинейности, когда на их вход поступает сигнал вида:
![]() ,
(97)
,
(97)
где
![]() - постоянная составляющая основного
сигнала.
- постоянная составляющая основного
сигнала.
![]() , (98)
, (98)
![]() - функция смещения
входного сигнала;
- функция смещения
входного сигнала;
![]() - коэффициент
гармонической линеаризации.
- коэффициент
гармонической линеаризации.
![]() .
(99)
.
(99)
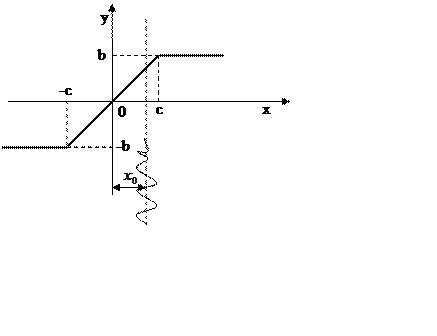 |
Рисунок 28
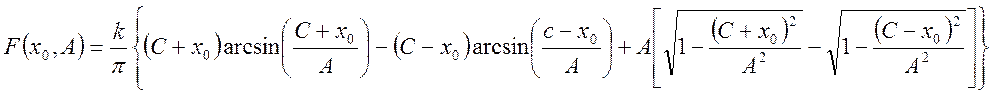 ,
,
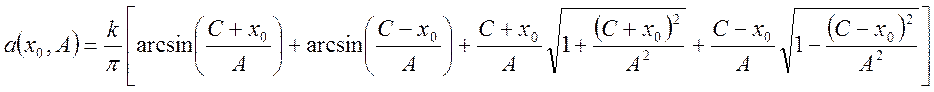 ,
(101)
,
(101)
при ![]() -
для однозначной нелинейности со смещением.
-
для однозначной нелинейности со смещением.
Для двухзначной нелинейности
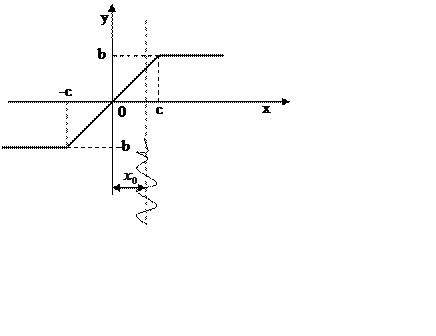 |
Рисунок 29
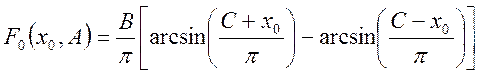 , (102)
, (102)
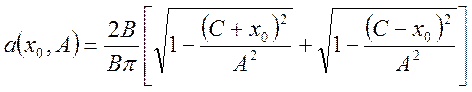 ,
(103)
,
(103)
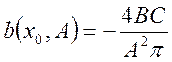 .
(104)
.
(104)
В нелинейных системах при недостаточном уровне подавления линейной части высших гармоник, необходимо учитывать дополнительные гармонические составляющие – автоколебания. При этом эквивалентная передаточная функция зависит от двух сигналов: частотного или многочастотного сигналов. Использование таких передаточных функций в нелинейных системах целесообразно, если требуется оценить влияние высших гармоник на появление автоколебаний.
Например: если в системе на первой гармонике открывают автоколебания, а действие третей появится.
Пусть на вход двузначной нечетной нелинейности поступает сигнал:
![]() ,
(106)
,
(106)
где
![]() - сдвиг фазы третьей гармоник.
- сдвиг фазы третьей гармоник.
Тогда на выходе
![]() .
(107)
.
(107)
Пусть ![]() ,
,
![]() ,
(108)
,
(108)
где
![]() и
и ![]() -
коэффициенты линеаризации по первой и третьей гармонике.
-
коэффициенты линеаризации по первой и третьей гармонике.
![]() .
(109)
.
(109)
Статическая линеаризация существенных нелинейных элементов
В системах в реальных условиях эксплуатации на вход существенных нелинейных элементов, наряду с детерминированием, поступают и случайные сигналы.
Существенные строгие методы анализа нелинейных систем со случайными сигналами требует учета закона распределения случайных величин, что приводит к громоздким вычислениям, затрудняющим процесс проектирования. Поэтому в инженерной практике принять использование приближенными методами. Методы статической линеаризации, сущность которого состоит в замене нелинейного элемента – статической линеаризованным. То есть однозначно нечетная нелинейная характеристика заменяет линеаризованность.
![]() , (110)
, (110)
![]() , (111)
, (111)
где
![]() - коэффициент по математическому
ожиданию;
- коэффициент по математическому
ожиданию;
![]() - математическое
ожидание;
- математическое
ожидание;
![]() - коэффициент,
при центральной случайной составляющей.
- коэффициент,
при центральной случайной составляющей.
![]() ,
(112)
,
(112)
где
![]() - подбирается таким образом, чтобы
максимально приблизить значение
- подбирается таким образом, чтобы
максимально приблизить значение ![]() к
к ![]() .
.
При статической линеаризации существует два подхода определения коэффициентов статической линеаризации.
1.
![]() ,
(113)
,
(113)
![]() .
(114)
.
(114)
2. Коэффициенты статической линеаризации выбирают из
условия минимума квадрата ошибки от замены ![]() на
на
![]() .
.
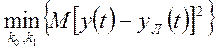 ,
(115)
,
(115)
где
![]() и
и ![]() находятся
из уравнения.
находятся
из уравнения.
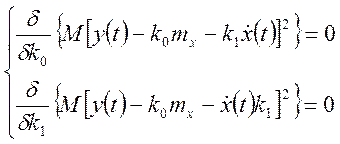 ,
(116)
,
(116)
Пример.
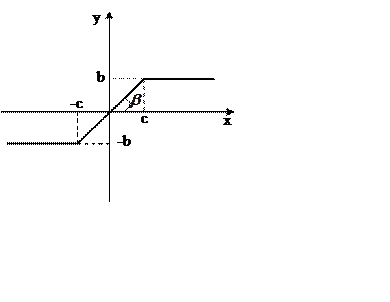 |
Рисунок 30
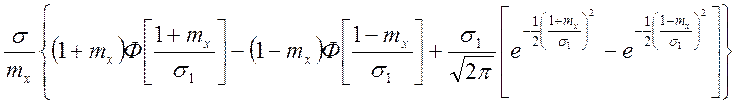 , (117)
, (117)
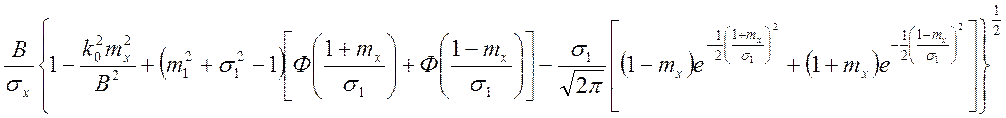 .
.
(118)
Совместная гармоническая и статическая линеаризация
При поступлении на вход нелинейного элемента сумма двух сигналов периодического случайного:
![]() .
(119)
.
(119)
Коэффициенты линеаризации являются периодическими функциями времени, то есть
![]() . (120)
. (120)
Применить выражение (120) совместную гармоническую и статическую линеаризацию, получит приблизительную зависимость:
![]() , (121)
, (121)
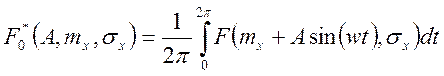 , (122)
, (122)
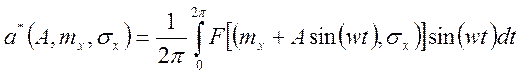 , (123)
, (123)
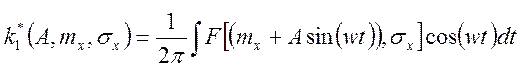 . (124)
. (124)
Выражение (110), (114), (115) представляет собой
усредненные за период ![]() значение гармонической
составляющей передаточной функции и статических коэффициентов.
значение гармонической
составляющей передаточной функции и статических коэффициентов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.