В дальнейшем сравнение формулы для определения коэффициентов линеаризации простейших нелинейностей при подаче на их вход периодических сигналов: синусоидального, треугольного, покажем целесообразность применения получаемых эквивалентных передаточных функций.
Перейдем к распределению обобщенного метода описания коэффициентов линеаризации на двухзначные нелинейности.
В этом случае, учитывая соотношение (50) и (52), можно записать:
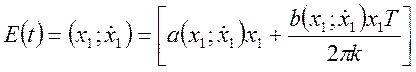 ,
(57)
,
(57)
Уравнение (52) примет вид
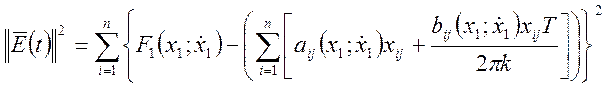 .
(58)
.
(58)
Коэффициент линеаризации определим (58) ![]() ,
, ![]() .
.
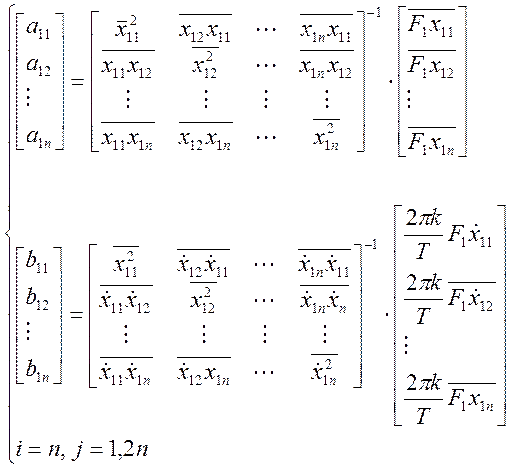 ,
(59)
,
(59)
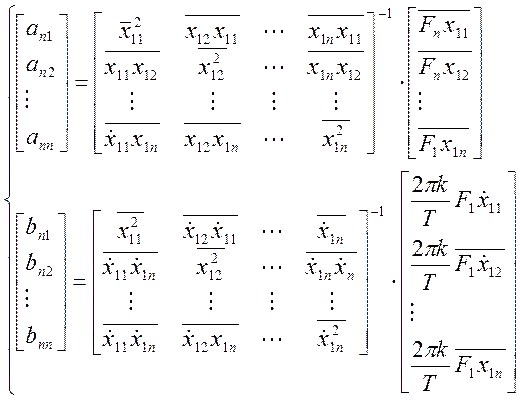 .
(60)
.
(60)
Пример. Определить коэффициент линеаризации двузначной нелинейности, когда на ее вход поступает первая гармоника синусоидального сигнала и имеет один вход. Из системы матриц (60), получим:
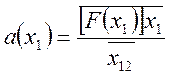 ,
(61)
,
(61)
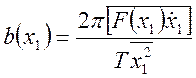 .
(62)
.
(62)
В данном примере входной сигнал запишем в виде:
![]() ,
(63)
,
(63)
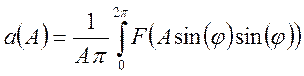 ,
(64)
,
(64)
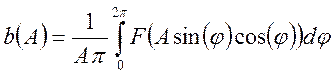 . (65)
. (65)
Когда для двузначной нелинейности общая эквивалентная функция:
![]() .
(66)
.
(66)
Гармоническая линеаризация типовых нелинейных элементов
Классическая – предлагает, что сигнал, снимаемый с выхода нелинейности, является периодическими и имеют основную частоту с частотой синуса входного сигнала. В результате этого допущения при нахождении эквивалентных передаточных функций или коэффициентов гармонической линеаризации учитывают только первую гармонику, а влияние высших корней пренебрегают. Это справедливо для систем, линейная часть которых является низкочастотной и подавляет колебание высоких частот.
Пусть на вход однозначной нелинейности поступает сигнал:
![]() .
(69)
.
(69)
Тогда выходной сигнал:
![]() .
(70)
.
(70)
Или
![]() .
(71)
.
(71)
Запишем выражение (71) через коэффициенты гармонической линеаризации.
![]() ,
(72)
,
(72)
![]() ,
(73)
,
(73)
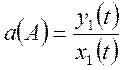 ,
(74)
,
(74)
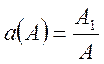 .
(75)
.
(75)
Коэффициент гармонической линеаризации однозначной нелинейности представляет собой коэффициент усиления, определяемый отношением амплитуды первой гармоники выходного сигнала к гармонике входного сигнала.
При гармонической линейности двузначной нелинейности, выходной сигнал имеет вид:
![]() ,
(76)
,
(76)
где
![]() - сдвиг фазы, зависящий от величины
амплитуды входного сигнала.
- сдвиг фазы, зависящий от величины
амплитуды входного сигнала.
![]() ,
(78)
,
(78)
![]() ,
(79)
,
(79)
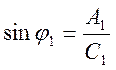 ,
(80)
,
(80)
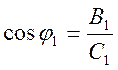 (81)
(81)
![]() ,
(82)
,
(82)
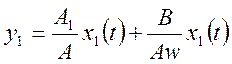 ,
(83)
,
(83)
![]() , –
эквивалентная функция.
(84)
, –
эквивалентная функция.
(84)
![]() ,
(85)
,
(85)
![]() ,
(86)
,
(86)
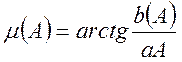 .
(87)
.
(87)
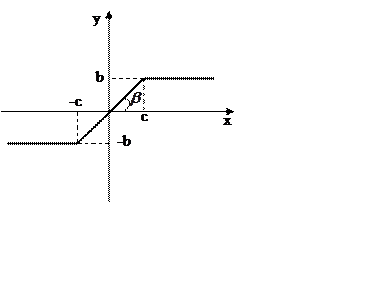 |
Рисунок 17
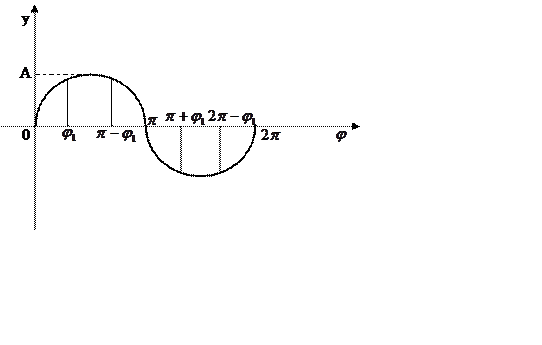 |
Рисунок 18
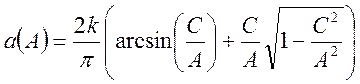 ,
(88)
,
(88)
![]() .
.
 |
Рисунок 19
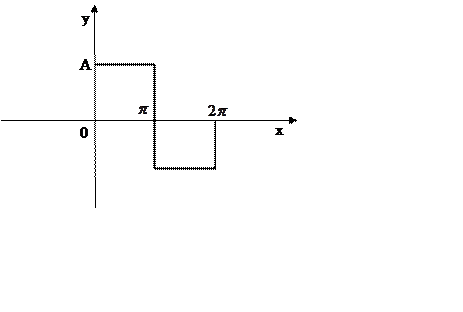 |
Рисунок 20
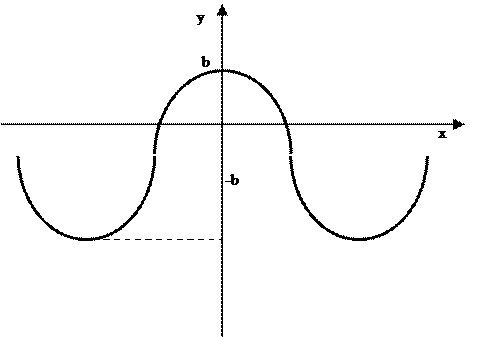 |
Рисунок 21
 |
Рисунок 22
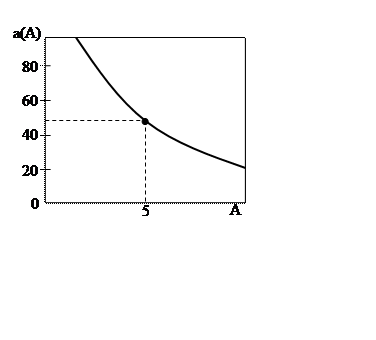 Шаблоны
Шаблоны
Рисунок 23
Двузначная нелинейность
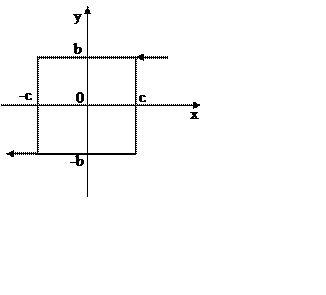 |
Рисунок 24
 |
Рисунок 25
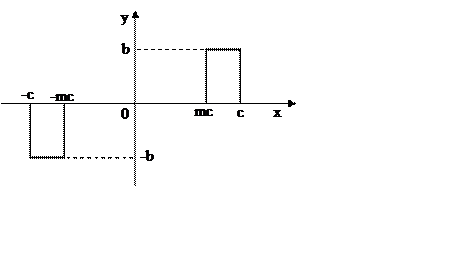 |
Рисунок 26
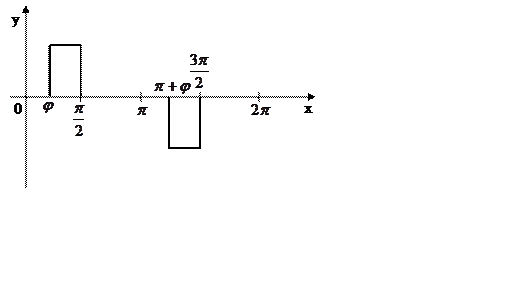 |
Рисунок 27
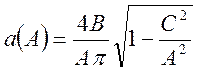 ,
(89)
,
(89)
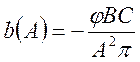 ,
(90)
,
(90)
![]() ,
,
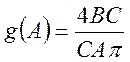 , (91)
, (91)
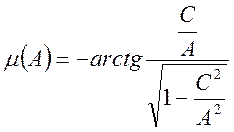 ,
(92)
,
(92)
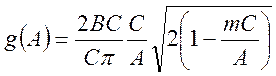 ,
(93)
,
(93)
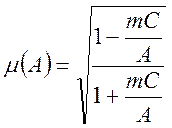 ,
(94)
,
(94)
при ![]() ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.