Математическое моделирование систем и процессов. Часть 3: Методические указания к выполнению лабораторных работ и самостоятельной работы

Н. В. ГОЛУБЕВА

МАТЕМАТИЧЕСКОЕ  МОДЕЛИРОВАНИЕ  СИСТЕМ  И

  ПРОЦЕССОВ

ЧАСТЬ 3

ОМСК  2008

Министерство транспорта Российской Федерации

Федеральное агентство железнодорожного транспорта

Омский государственный университет путей сообщения

_________________________

Н. В. Голубева

МАТЕМАТИЧЕСКОЕ  МОДЕЛИРОВАНИЕ  СИСТЕМ  И

  ПРОЦЕССОВ

Часть  3

Утверждено редакционно-издательским советом  университета

в качестве  методических  указаний  к выполнению лабораторных  работ  и

самостоятельной  работы  по дисциплине

 «Математическое  моделирование систем  и процессов»

Омск  2008

УДК 681.32.06:518.5

ББК 22.311я7

Г62

Математическое моделирование систем и процессов. Часть 3: Методи-ческие указания к выполнению лабораторных  работ и самостоятельной работы по дисциплине «Математическое моделирование систем и процессов» / Н. В. Голубева; Омский гос. ун-т путей сообщения. Омск, 2008. 32 с.

Рассматриваются принципы формирования математических моделей различных классов, пути решения некоторых типов задач, возникающих в процессе  математического моделирования и особенности их реализации в интегрированной среде  MathCAD.

Предназначены для студентов 2-го курса, обучающихся по направлению 657700 − «Системы обеспечения движения поездов» − по специальностям «Автоматика, телемеханика и связь на железнодорожном транспорте», «Электроснабжение железных дорог», по направлению 140100 − «Теплоэнергетика» − по специальностям «Промышленная теплоэнергетика», «Тепловые  электрические станции», «Энергообеспечение предприятий» и по направлению 657600 − «Подвижной состав железных дорог» − по специальности  «Локомотивы»,  для студентов заочного обучения, а также для обучения с использованием  дистанционных образовательных технологий.

Библиогр.: 5 назв. Табл. 2.  Рис. 2.

Рецензенты: доктор техн. наук, профессор  В. Н. Горюнов;

канд. техн. наук, доцент А. Т. Когут.

Омский гос. университет

путей  сообщения, 2008

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ

Математическое моделирование является важнейшим научным приемом, инструментом изучения окружающих объектов и явлений. Внедрение новых информационных технологий значительно повышает возможности  математического моделирования и делает его самым перспективным средством познания мира. Компьютерные математические системы  и пакеты, такие как Derive, MathCAD, Maple, Mathematica, MatLAB, позволяют  решать задачи математи-ческого  моделирования  процессов  и  устройств  различной физической  природы.

Методические указания (часть 3) включают в себя две лабораторные работы. В лабораторной  работе 9 рассматриваются принципы и особенности  реализации типовых моделей двух классов случайных последовательностей, используемых  при формировании стохастических моделей физических систем. Лабораторная работа 10 знакомит студента с одним из важных разделов теории приближений − задачей  интерполяции, часто возникающей  в процессе моделирования. Рассматриваются особенности применения различных видов интерполяционных функций и средства решения задачи интерполяции в системе MathCAD.

В процессе выполнения лабораторных работ студент должен уяснить важность правильной постановки задачи, выбора метода ее решения и способа отображения результатов моделирования и умения правильно интерпретировать их.

Методические указания предназначены для студентов 2-го курса очного и заочного обучения, а также для обучения с использованием  дистанционных образовательных технологий.

Лабораторная  работа  9

РЕАЛИЗАЦИЯ  ТИПОВЫХ  МОДЕЛЕЙ  СЛУЧАЙНЫХ

ПОСЛЕДОВАТЕЛЬНОСТЕЙ  ПРИ  ФОРМИРОВАНИИ 

СТОХАСТИЧЕСКИХ  МОДЕЛЕЙ  ФИЗИЧЕСКИХ  СИСТЕМ

9.1.Постановка  задачи

Физическая система, функционирующая в условиях влияния внутренних и внешних случайных факторов (шумов), наиболее адекватно (достоверно) может быть описана  стохастической  математической  моделью.

          В отличие от  детерминированной модели стохастическая модель учитывает случайный характер процессов в моделируемой системе. Во многих задачах это реализуется посредством включения в математическую модель случайного мешающего процесса (шума) ω(t), воздействующего на вход системы аддитивно или мультипликативно.

В дискретных стохастических моделях понятие «случайный процесс»  заменяется понятием  «случайная последовательность».

          В связи с этим на этапе исследования и аппробации сформированной стохастической модели важное значение приобретают алгоритмы и инструменты реализации  типовых моделей случайных процессов (случайных последовательностей). Для этой цели в любой среде программирования созданы генераторы случайных  чисел.

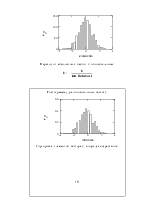
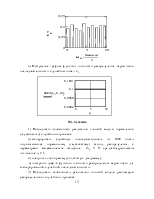
          Часто  в  процессе  моделирования  приходится  решать следующую задачу: определять характер  распределения некоторой случайной  величины  x по результатам ее многократных измерений (наблюдений) . Решение основано на построении гистограммы – ступенчатого графика, аппроксимирующего по результатам  измерения случайной величины плотность ее распределения. Диапазон значений случайной  величины  разбивают на некоторое количество интервалов, а затем  подсчитывают частоту (процент) попадания данных в каждый интервал. Таким образом, гистограмма отображает частоту  попадания значений случайной  величины  в каждый  из интервалов.

9.2 . Информация  к  выполнению  задания 1

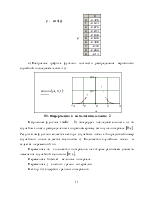
          Встроенная функция rnorm(nn,m_y,σ_y) генерирует последовательность случайных чисел, распределенных по нормальному закону с математическим  ожиданием  m_y и среднеквадратическим отклонением σ_y. Результатом функции является  вектор  y  из  nn  случайных  чисел  y_i.

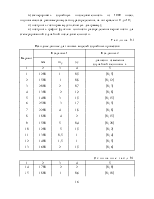
Для вывода графика, иллюстрирующего распределение случайных чисел, необходимо воспользоваться инструментом «Декартов график». При форматировании графика следует  установить параметры: тип – «точки», толщина – «2».

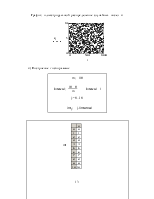
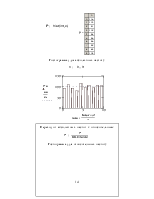
Для  построения  гистограммы  вводятся переменные:

m – количество интервалов, на которые разбиваем диапазон изменения случайной  величины ;

y min – минимальное  значение случайной  величины y, определяемое с помощью  встроенной  функции  min(y) (после  ввода шаблона функции min(y) удалите из диалогового окна «Вставка функции» лишние маркеры ввода, оставив один);