Математическое моделирование систем и процессов. Часть 3: Методические указания к выполнению лабораторных работ и самостоятельной работы, страница 4

Сплайн – это функция, образуемая из последовательности сопряженных (состыкованных в узлах) полиномов. На каждом i-м интервале [x_i-1, x_i] сплайн-функция представляется  i-м  полиномом, определенным для данного конкретного интервала. Полиномы соседних интервалов стыкуются так, чтобы функция и соответствующие ее производные были непрерывны. Наиболее популярна интерполяция кубическими сплайнами.

Кубический сплайн – это кусочнополиномиальная функция, которая образуется путем стыковки (сшивания) в узлах полиномов третьей степени. При этом на i-м интервале [x_i-1, x_i] функция  интерполируется кубическим  полиномом:

                 (10.16)

Для  всего интервала интерполяции [x₀; x_n] необходимо определить n кубических  полиномов, отличающихся  коэффициентами

Коэффициенты полиномов (10.16) сплайна определяются из следующих условий:

каждый i-й  полином проходит через два соседних узла x_i-1 и x_i, т. е. значения сплайна  равны значениям заданной аппроксимируемой функции  в узлах интерполяции (условие интерполирования);

первая  производная сплайн-функции S(x) непрерывна в узлах интерполяции (условие гладкости функции);

вторая производная сплайн-функции S(x) непрерывна в узлах интерполяции (условие гладкости первой производной функции);

граничные условия, задающие поведение сплайн-функции S(x) в граничных точках интервала интерполяции x₀ и x_n (определяются  постановкой задачи).

Достоинством интерполирования кубическими сплайнами является его сходимость. При неограниченном возрастании числа узлов последовательность получаемых сплайн-функций сходится к заданной интерполируемой функции  Использование сплайнов обеспечивает получение наиболее гладкой интерполяционной функции.

10.5. Информация  к  выполнению  задания  1

Матрица  MX формируется из элементов  вектора X согласно выражению (10.7).

Ypol(xx) −это приближенное значение функции , определяемое с помощью интерполяционного полинома в каноническом виде (по формуле (10.9)). Переменная xx задается как ранжированная  для построения графика интерполирующей функции на заданном интервале интерполяции [x₀; x_n].

Пример выполнения задания 1

Пусть функция   задана таблицей значений y_i, определенных  в узлах  x_i:

x	0,5	2,4	5,3	7,9	10	11,6	13	16	17,7	20
y	6,252	3,831	−9	0,904	2	2,735	5	1,721	−4	−6,108

Построить интерполяционный полином в каноническом виде и определить приближенное  значение функции  в точках  xx1 = 3,7;  xx2 = 8,35;  xx3 = 18,9.

1. Задание вектора значений узлов интерполяции X и вектора значений исходной функции Y:

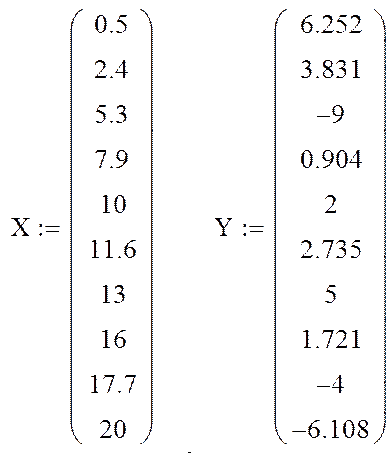
2. Формирование матрицы  MX:

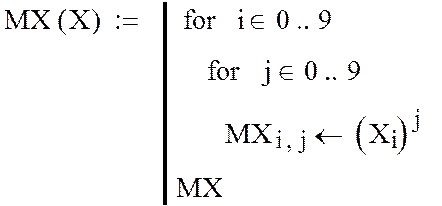
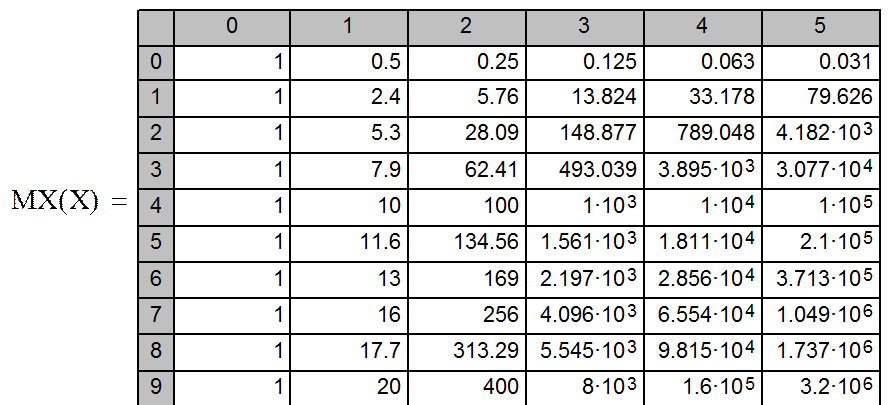
3.  Определение коэффициентов интерполяционного полинома:

 

                                                      

    

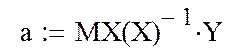
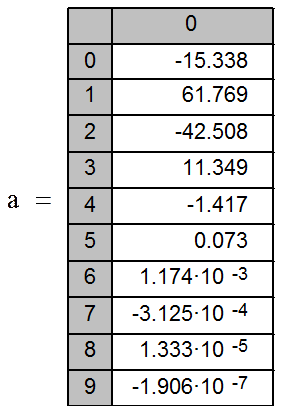
4. Определение приближенного значения функции  в точках xx1, xx2, xx3 c помощью интерполяционного полинома согласно формуле (10.9):

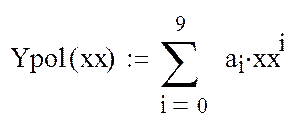
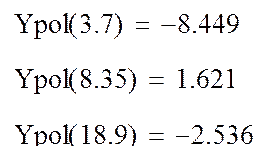
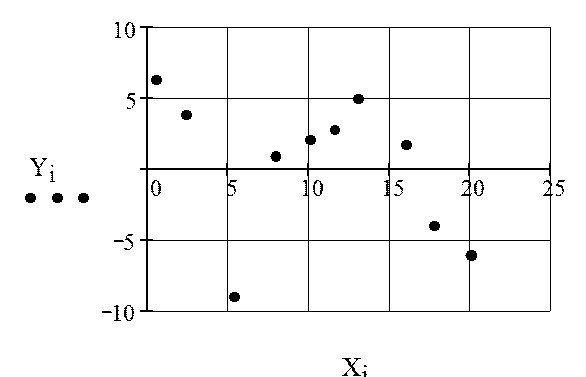
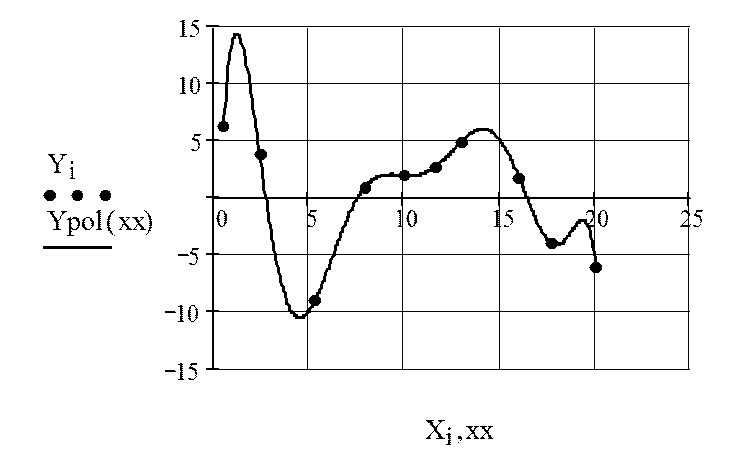
5. Отображение на графике исходной (интерполируемой) функции :

                       

  

6. Построение графика интерполирующей кривой:

10.6.  Информация  к  выполнению  задания  2

L(X,Y,xx) − это приближенное значение функции  в точке xx, определяемое с помощью интерполяционного полинома Лагранжа (по формуле (10.15)). Алгоритм вычисления приближенного значения функции в произвольной точке xx с помощью интерполяционного полинома Лагранжа представлен на рис. 10.2.

Пример выполнения задания 2

1. Вычисление приближенного значения функции в произвольной точке xx с помощью интерполяционного полинома  Лагранжа:

 

…

2. Определение приближенного значения функции  в точках  xx1, xx2, xx3  c помощью интерполяционного полинома  Лагранжа:

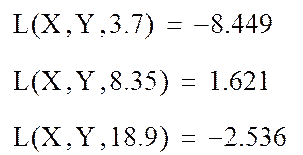
3. Построение графика интерполирующей кривой:

10.7.  Информация  к  выполнению  задания  3

Пример выполнения задания 3

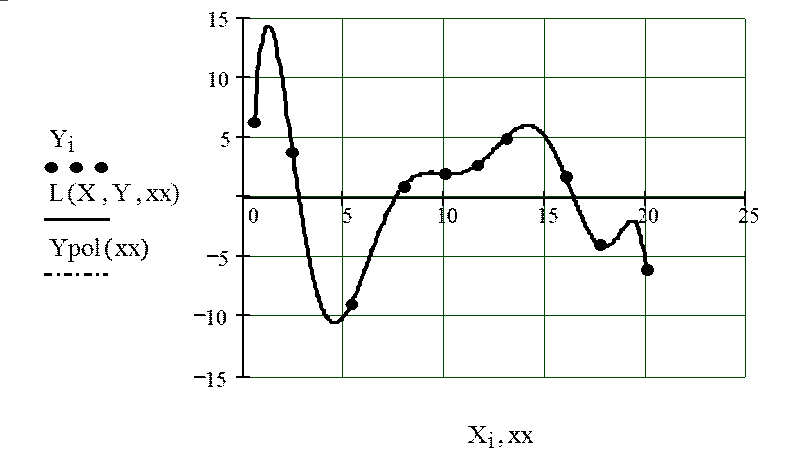
Сопоставление кривых интерполирующих функций, полученных по интерполяционным формулам (10.9) и (10.15):

 

10.8.  Информация  к  выполнению  задания  4

Встроенная функция  cspline(X,Y) вычисляет вектор вторых производных функции , используя приближение сплайн-функции в узлах кубическим полиномом.

Встроенная функция interp(Pr,X,Y,xx) вычисляет значение функции  в произвольной точке xx с помощью интерполяции сплайн-функцией.

Встроенные функции lspline(X,Y) и pspline(X,Y) определяют вектор вторых производных, используя соответственно линейное и квадратичное  (параболическое) приближения  сплайн-функции  в узлах.

Пример выполнения задания 4

1. Определение вектора вторых производных с приближением в узлах кубическим  полиномом:

2. Определение приближенного значения функции  в произвольной точке  xx с помощью интерполяции сплайн-функцией:

3. Определение приближенного значения функции  в точках  xx1, xx2, xx3:

 

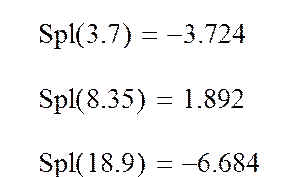
4. Построение интерполяционных кривых с помощью сплайн-функции и полинома  Лагранжа:

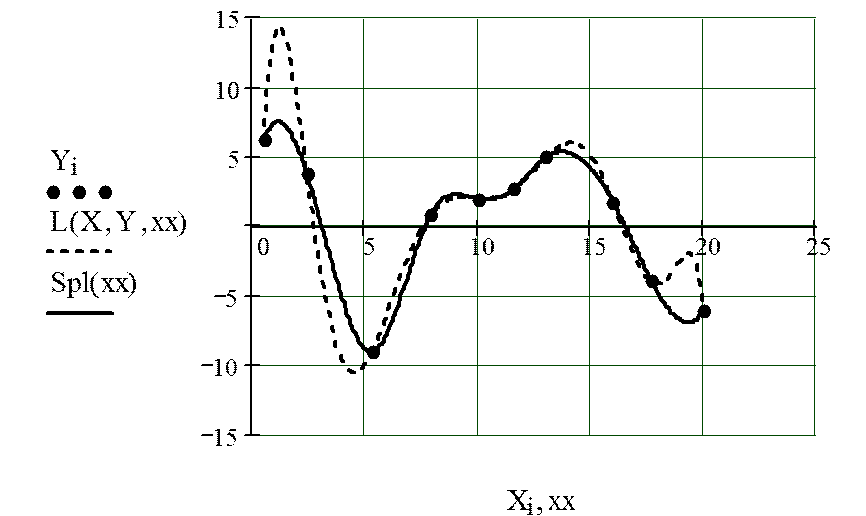
5. Построение графиков трех сплайн-функций, полученных при разных типах  приближений кубического сплайна  в узловых точках:

 

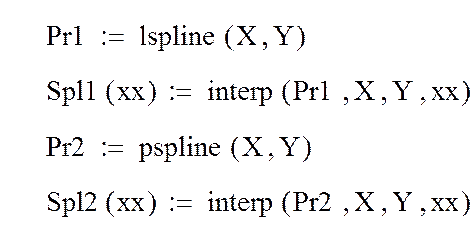
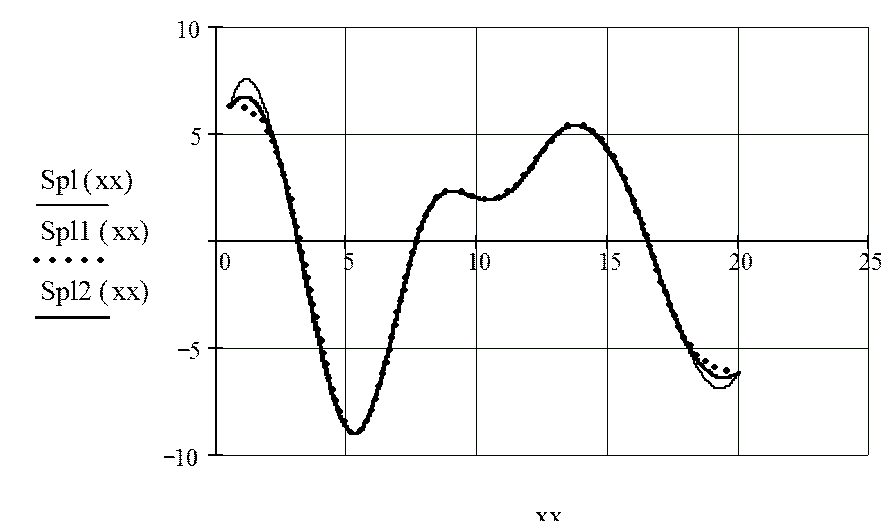
10.9. Задания

1. Для функции  заданной таблично, построить интерполяционный полином  в  каноническом  виде  и определить  приближенное  значение функции в  точках  xx1, xx2, xx3. Построить график интерполяционной функции.