Математическое моделирование систем и процессов. Часть 3: Методические указания к выполнению лабораторных работ и самостоятельной работы, страница 2

y max – максимальное  значение случайной величины y, определяемое с помощью  встроенной  функции  max(y);

linterval – величина  интервала (все интервалы имеют одинаковую величину);

k – счетчик границ  интервалов.

          Вектор interval  содержит  значения  границ  интервалов, где k-я граница  определяется  соотношением:

          Встроенная  функция  hist(cinterval,y) определяет вектор h, элементами  которого являются абсолютные частоты  попадания значений случайной величины  y  в соответствующий  интервал.

          Вектор  cinterval  содержит середины  интервалов.

          Переменная  n  задаeт порядковый номер интервала.

Для построения гистограммы  используется инструмент «Двумерный декартов график». В диалоговом окне «Форматирование» на  вкладке «Графики» в поле  «Тип» следует  установить параметр «столбцы».

Необходимо  проконтролировать правильность установки пределов по оси x, они должны быть близки к значениям y min (нижний предел) и  y max  (верхний предел). По оси  y нижний предел должен быть равен нулю.

Встроенная функция sort(y) упорядочивает элементы вектора y по возрастанию.

Переменная  i – счeтчик  чисел  случайной  последовательности  у.

Встроенная функция dnorm(y_k,m_y,σ_y) определяет плотность распределения  вероятностей случайной  величины  у,  распределeнной  по нормальному  закону.

Пример выполнения задания 1

а) Генерирование  случайной  последовательности  у  из 1000  чисел (nn =1000), подчиняющихся нормальному (гауссовскому) закону распределения, с параметрами  m_y = 0  и  σ_y = 1:

   

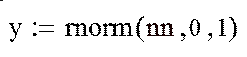
Вывод  вектора  случайных чисел  y:

Построение графика, иллюстрирующего распределение случайных чисел  y:

                              

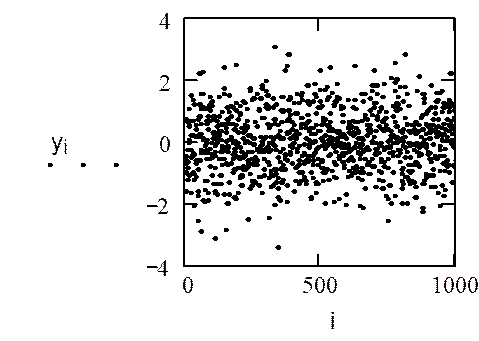
б) Построение  гистограммы:

   

       

 

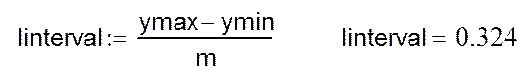
  Гистограмма (для абсолютных частот)

    

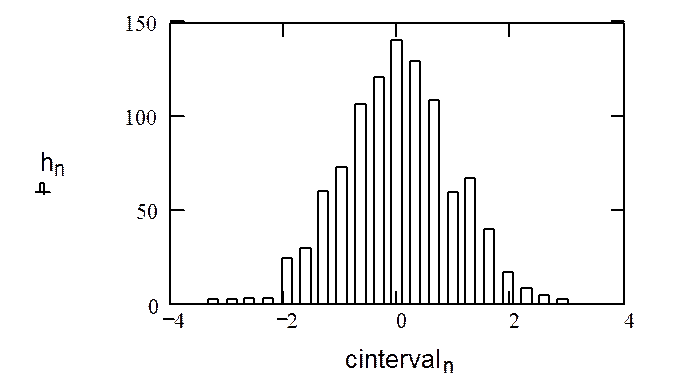
Переход от  абсолютных  частот  к  относительным:

 

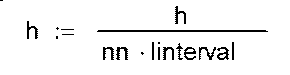
Гистограмма (для относительных частот):

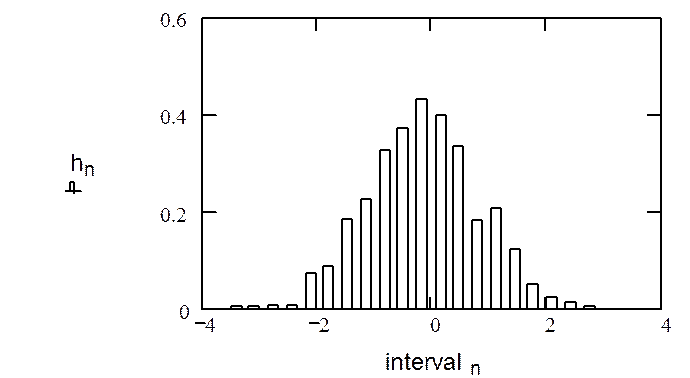
Сортировка  элементов  вектора y  в порядке возрастания:

                                

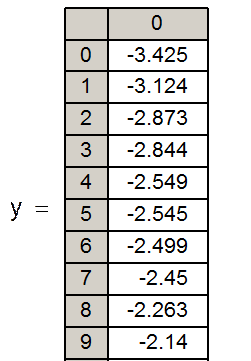
в) Построение графика функции плотности распределения вероятности случайной  последовательности  y_i:

     

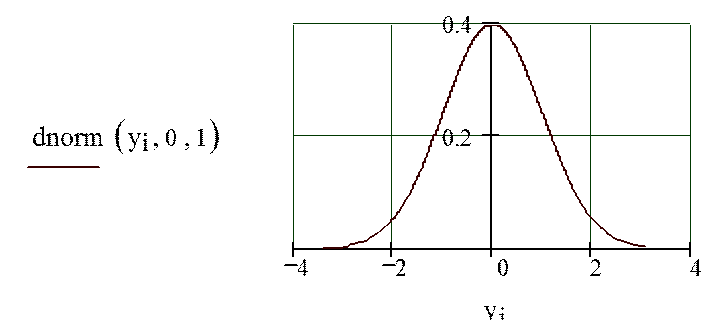
9.3 . Информация  к  выполнению задания  2

Встроенная функция rnd(c − 0) генерирует последовательность из nn случайных чисел, распределенных по равномерному закону на интервале . Результатом функции является вектор x случайных чисел x_i (порядковый номер случайного числа задается счетчиком i). Количество случайных чисел  x_i задается  переменной  nn.

Переменная  m – количество  интервалов, на которые разбиваем диапазон изменения случайной  величины .

Переменная  linterval – величина  интервала.

Переменная  j – счетчик  границ  интервалов.

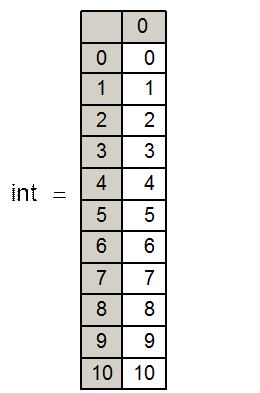
Вектор  int  содержит границы интервалов.

P – вектор частот попадания случайных чисел x_i в интервалы гистограммы.

Переменная  n  задает порядковый номер интервала.

При построении гистограммы по оси абсцисс откладываются середины  интервалов:

.

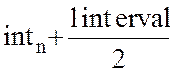Встроенная функция dunif(x_i,0,c) определяет плотность распределения вероятностей случайной величины x, распределенной по равномерному закону в диапазоне .

Пример выполнения задания 2

а) Генерирование случайной последовательности x из 1000 чисел, подчиняющихся  равномерному  закону  распределения в диапазоне :

    

 

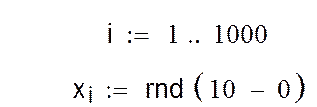
Вывод  вектора случайных чисел  x:

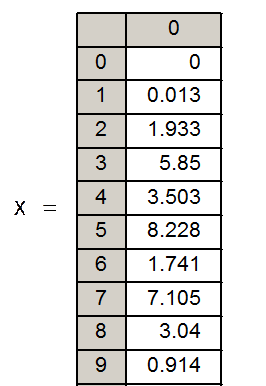
График,  иллюстрирующий  распределение  случайных  чисел  x:

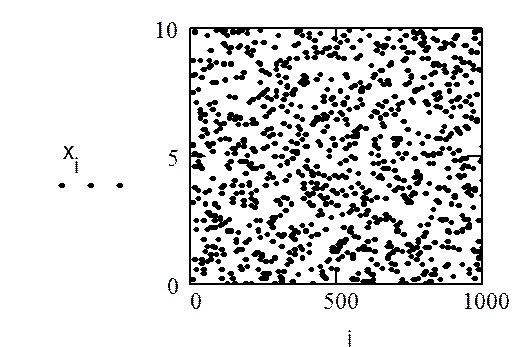
б) Построение  гистограммы:

    

     

 

                        

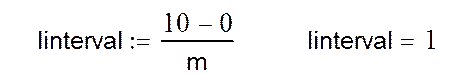
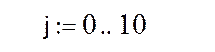
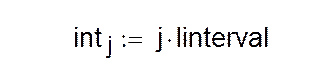
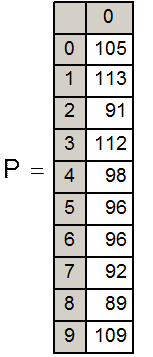
Гистограмма (для абсолютных частот):

 

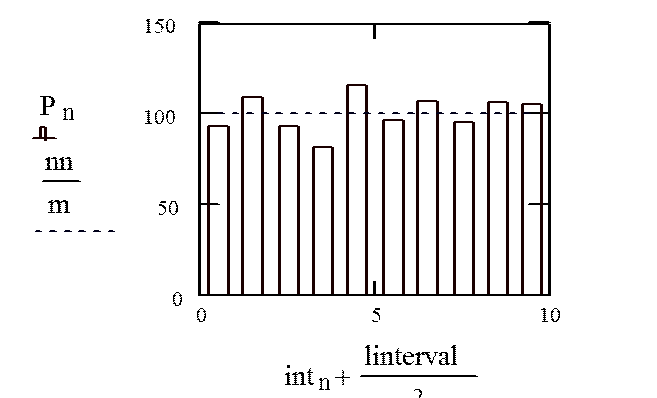
Переход от  абсолютных  частот  к  относительным:

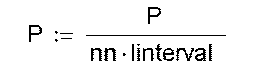
 Гистограмма (для относительных частот):

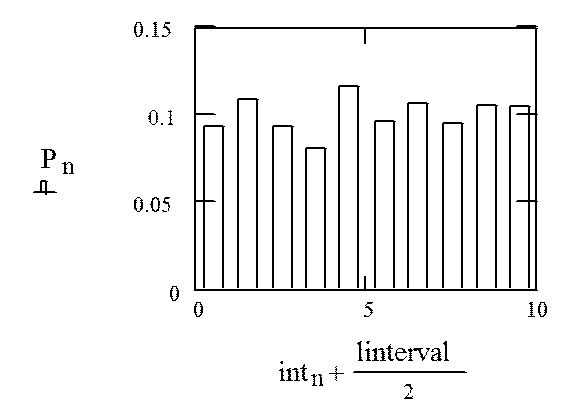
в) Построение графика функции плотности распределения вероятности последовательности  случайных чисел  x_i:

                               

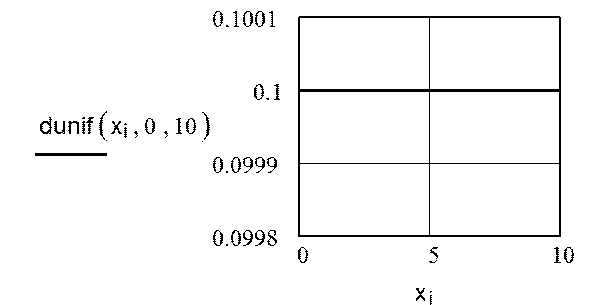
9.4. Задания

1) Исследовать особенности реализации типовой модели нормального (гауссовского) случайного процесса:

a) cгенерировать случайную последовательность из 1000 чисел, подчиняющихся нормальному (гауссовскому) закону распределения, с параметрами: математическое ожидание  m_y = 0; среднеквадратическое отклонение σ_y = 1;

б) построить гистограмму (столбчатую диаграмму);

в) построить график функции плотности распределения вероятности для сгенерированной случайной последовательности.

2) Исследовать особенности реализации типовой модели равномерно распределенного случайного процесса:

a) сгенерировать случайную последовательность из 1000 чисел, подчиняющихся  равномерному закону распределения, на интервале от 0  до 10;

б) построить гистограмму (столбчатую диаграмму);

в) построить график функции плотности распределения вероятности для сгенерированной случайной последовательности.

Таблица 9.1

Исходные данные для типовых моделей случайных процессов

Вариант	К заданию 1			К заданию 2
	nn			диапазон  изменения случайной  величины  x
1	2	3	4	5
1	1200	1	0,5	[0; 5]
2	1500	−1	0,8	[0; 12]
3	2000	2	0,7	[0; 3]
4	1300	−2	1,2	[0; 8]
5	1400	3	1,5	[0; 15]
6	2500	−3	1,7	[0; 5]
7	2200	4	1,8	[0; 8]
8	1800	−4	2	[0; 15]
9	1500	5	0,4	[0; 20]
10	1200	−5	1,5	[0; 2]
11	1300	0,5	1	[0; 4]
12	1400	1,5	1	[0; 5]
13	1600	2	1,5	[0; 6]