Математическое моделирование систем и процессов. Часть 3: Методические указания к выполнению лабораторных работ и самостоятельной работы, страница 3

Окончание табл.  9.1

1	2	3	4	5
14	1700	−2	2	[0; 9]
15	1800	−1	0,6	[0; 10]
16	1900	1	0,7	[0; 8]

Лабораторная  работа  10

МАТЕМАТИЧЕСКОЕ  МОДЕЛИРОВАНИЕ.

РЕШЕНИЕ  ЗАДАЧИ  ИНТЕРПОЛЯЦИИ

10.1. Постановка  задачи

В процессе математического моделирования как на стадии формирования модели, так и на этапе решения модели часто появляется необходимость аппроксимировать ту или иную функциональную зависимость. Под  аппроксимацией понимают приближение (приближенную замену) исходной функции другой функцией, более простой  и легко вычисляемой.

Решение многих задач электроники, электротехники, физики, радиотехники, теории автоматического управления предполагает аппроксимацию вольтамперных характеристик нелинейных элементов, амплитудно-частотных и фазочастотных  характеристик фильтров, усилителей и т. д. Аппроксимация широко используется в научных исследованиях для представления (описания) физических закономерностей на основе полученных экспериментально (эмпирических) данных. В некоторых задачах, связанных со сложными многомерными моделями, приходится иметь дело с функциями, заданными громоздкими аналитическими  выражениями. Анализ таких функций затруднен, вычислительные операции над ними трудоемки. Проблема решается с помощью аппроксимации  данной функции другой функцией с такими свойствами, которые упрощают  работу  исследователя.

Выбор критерия близости (критерия согласия) аппроксимирующей и аппроксимируемой функций определяется постановкой задачи. Если в качестве критерия близости принято условие совпадения аппроксимирующей и аппроксимируемой функций в заданном ряде дискретных точек (в узлах), то приходят к задаче  интерполяции или  интерполирования. Основная задача  интерполяции – нахождение  значения таблично заданной функции в промежуточных точках между узлами.  Если требуется определить значение функции в точке, находящейся за пределами заданного интервала аппроксимации, то решают  задачу  экстраполяции.

Конкретизируем задачу интерполяции. Пусть функция  задана таблицей значений, определенных  в точках   (узлах):

                  (10.1)

Требуется построить интерполирующую (аппроксимирующую) функцию  принадлежащую известному  классу и принимающую в узлах интерполяции те же значения, что и заданная функция   т. е. такую, что

                   (10.2)

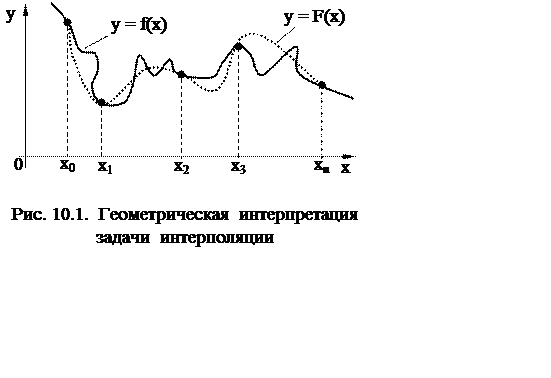Геометрически это означает, что надо построить кривую  определенного типа, проходящую через точки с координатами   (рис. 10.1).

В такой постановке задача интерполяции имеет бесчисленное множество ре-шений. Однозначное  решение можно получить, если  в  качестве аппроксимирующей функции  выбрать полином (многочлен)  степени не выше n, удовлет-воряющий  условиям:

                (10.3)

Полиномы имеют очевидные преимущества перед другими классами интерполирующих функций: они являются линейными функциями своих коэффициентов, их можно легко  вычислять, складывать, умножать, интегрировать и дифференцировать. 

В зависимости от решаемой задачи используют различные формы (формулы) представления интерполяционного полинома (в каноническом виде, формулы  Лагранжа, Ньютона, Стирлинга, Бесселя и т. д.)

10.2.  Интерполяция  полиномом  в каноническом  виде

          Пусть для функции  заданной таблично, требуется найти полином   для  которого будут выполняться  условия  интерполяции (10.3).

В качестве интерполирующей функции выберем полином  степени  n  в каноническом  виде:

                                (10.4)

Определим  коэффициенты   полинома (10.4). Для этого исходя из условия совпадения аппроксимирующей и аппроксимируемой  функций в  n + 1 узлах (10.3) составим  систему алгебраических уравнений

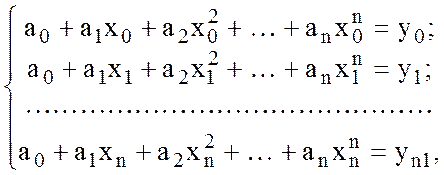                              (10.5)

которая  в  векторно-матричной форме имеет  вид:

                                                     (10.6)

где  – вектор свободных членов;  – вектор неизвестных  коэффициентов полинома;  MX – матрица  вида:

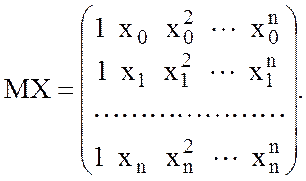                                      (10.7)

Так как среди узлов x_i  нет совпадающих, определитель системы (10.5) отличен от нуля, то данная система, а следовательно, и поставленная задача имеют единственное решение.

Решаем  систему (10.5)  матричным  методом:

                                              (10.8)

находим искомые коэффициенты  полинома .

Итак, интерполирующий полином найден. Теперь с его помощью можно определить приближенное значение заданной функции  в любой произвольной  точке  xx  интервала  интерполяции [x₀; x_n]:

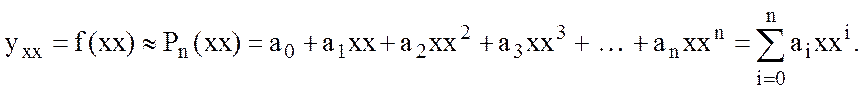  (10.9)

10.3.  Интерполяция  полиномом  Лагранжа

Лагранж предложил строить интерполирующий полином (далее полином  Лагранжа  обозначаем ) в виде линейной  комбинации полиномов  n-й степени:

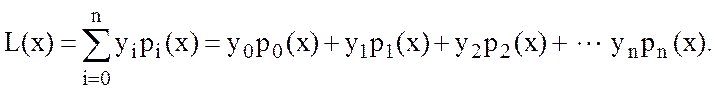       (10.10)

При этом требовалось, чтобы все полиномы  удовлетворяли условию:

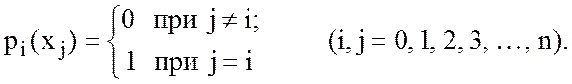                   (10.11)

Условие (10.11) означает, что каждый полином  должен обращаться в нуль во всех узлах интерполяции  кроме  i-го, в котором он примет значение, равное  единице. Таким образом, для  каждого  j-го узла  получим:

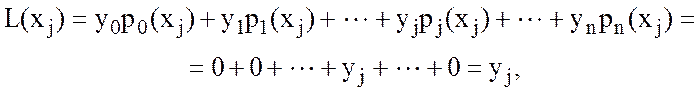          (10.12)

т. е. выполняются условия  интерполяции (10.3).

Легко доказать, что условию (10.11) удовлетворяет  полином:

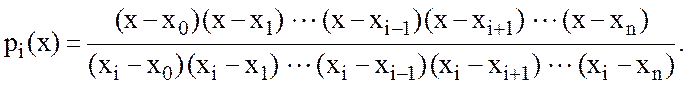          (10.13)

Следовательно, интерполяционный полином Лагранжа имеет  вид:

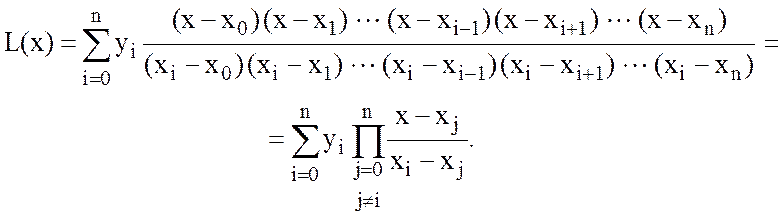   (10.14)

Для определения приближенного значения функции  в произвольной точке xx интервала  интерполяции [x₀; x_n] применяется интерполяционная формула Лагранжа:

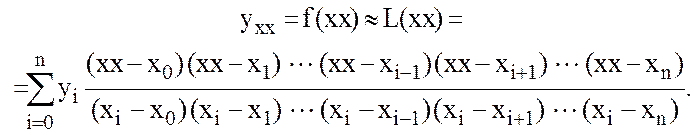          (10.15)

Алгоритм вычисления приближенного значения функции по интерполяционной формуле Лагранжа  (10.15) приведен на рис. 10.2.

10.4.  Интерполяция сплайнами