Реализация датчика случайных чисел с экспоненциальным законом распределения на основе стандартного датчика среды Matlab, имеющего равномерное распределение

Министерство образования и науки

Российской Федерации

СП ГУАП

КАФЕДРА № 43

ОТЧЕТ

ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

                                                      .

должность, уч. степень, звание                 подпись, дата                                      фамилия, инициалы

Отчет о лабораторной работе №2

Датчики случайных чисел. Построение гистограмм.

по курсу  «Компьютерное моделирование»

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР.     4539кф           ______________               Зоз В. Н.                                                                                                                           подпись, дата                      фамилия, инициалы

Санкт-Петербург

2009

Цель работы

Изучение алгоритмов получения на ЭВМ чисел с заданным законом распределения а также основных принципов построения гистограмм.  

В соответствии с вариантом 13 выбран равномерный закон распределения с параметром a=-15; b=-10:

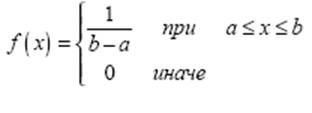
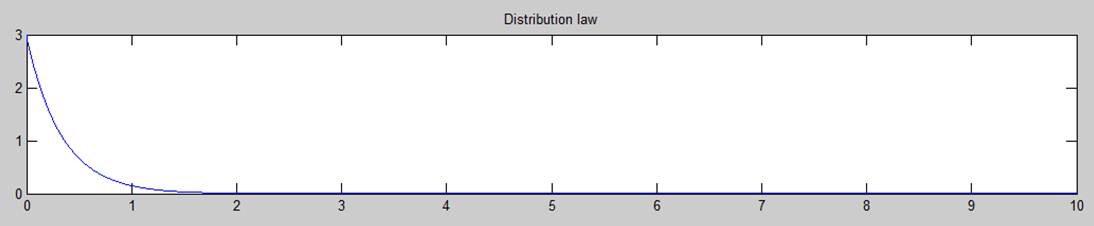
Рисунок 1 – график требуемого закона распределения

Описание разработанной программы

            Программа разработана для среды MatLAB. Текст программы с комментариями приведен ниже.

length = 100000;

base = rand(1, length);

a = -15;

b = -10;

lambda = 3;

k = 10;

UniAB = base .* (b - a) + a;

Exp = log(base) ./ lambda;

Norm = zeros(1, length);

for i = 1 : (length / 2)

    Norm(2 * i) = sqrt(-2 * log (base(i))) * sin(2 * pi * base(i+1));

    Norm(2 * i - 1) = sqrt(-2 * log (base(i))) * cos(2 * pi * base(i+1));

end

Erl = zeros(1, length);

for i = 1 : k

    temp = log(rand(1, length)) ./ lambda;

    Erl = Erl + temp;

end

% пик в k/lambda

figure

subplot(2,1,1);

stairs(UniAB, 'r');

subplot(2,1,2);

hist(UniAB,100);

figure

hold on

subplot(2,1,1);

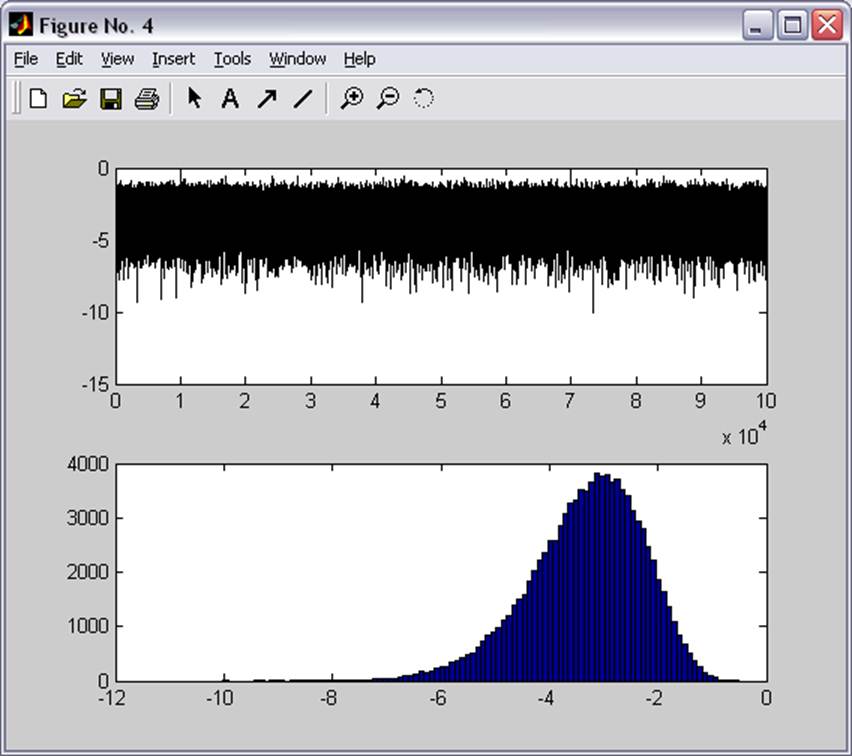
stairs(Exp, 'g');

subplot(2,1,2);

hist(Exp,100);

figure

hold on

subplot(2,1,1);

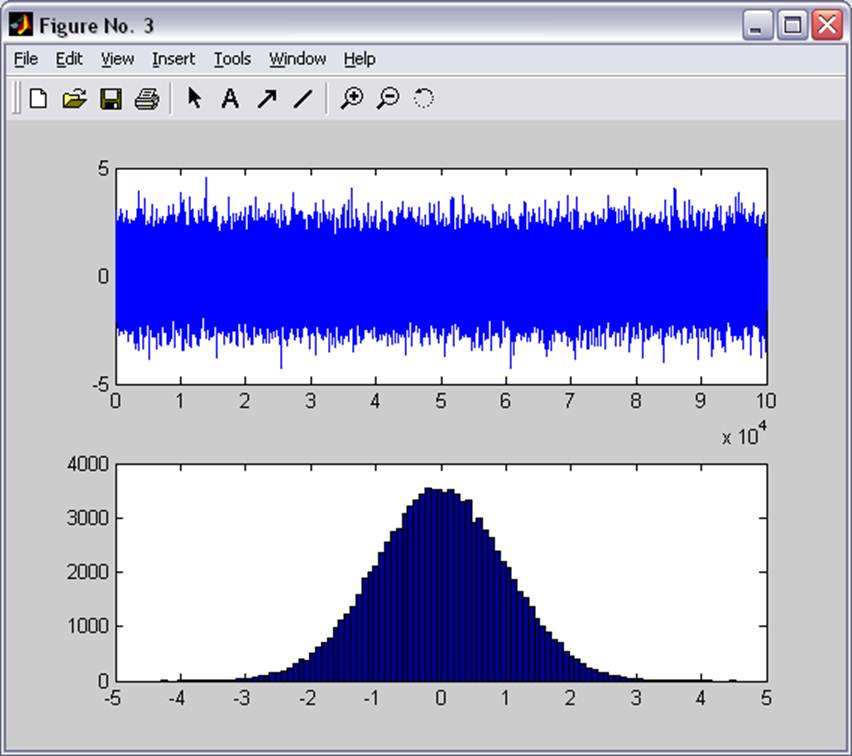
stairs(Norm, 'b');

subplot(2,1,2);

hist(Norm,100);

figure

hold on

subplot(2,1,1);

stairs(Erl, 'k');

subplot(2,1,2);

hist(Erl,100);
Гистограмма и функция распределения сформированной выборки

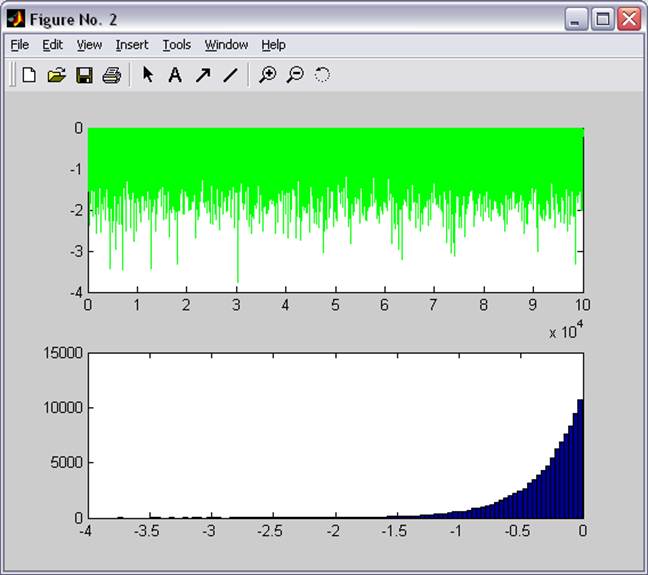
Рисунок 2 – гистограмма и функция распределения сформированной выборки

Графики зависимости оценок математического ожидания и дисперсии от объема выборки.

По оси x отмечена величина i: N_выб=10ⁱ. По оси x отмечены значения матожидания и дисперсии сформированных выборок соответствующего размера. Уровнем отмечены теоретические значения.

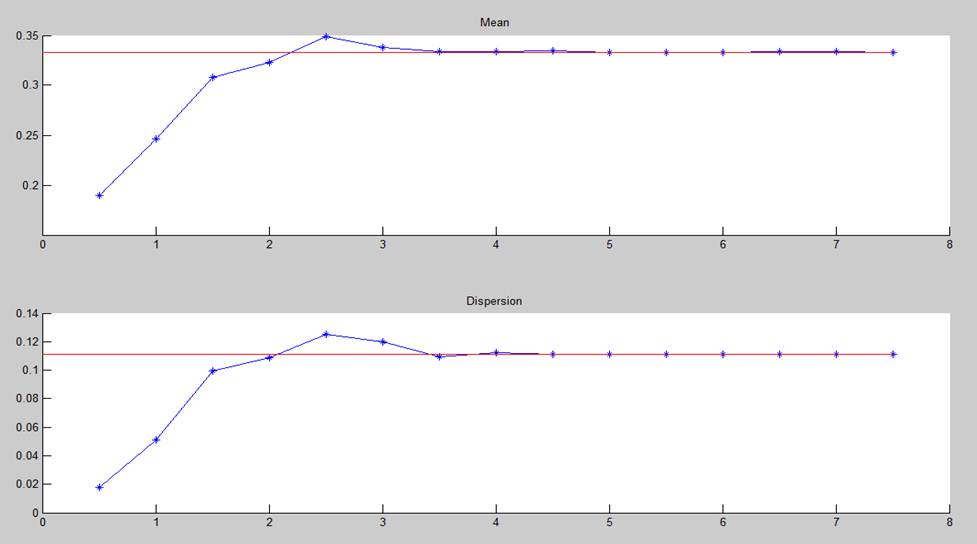
Рисунок 3 – математическое ожидание и дисперсия выборок разного объема

Вывод

В данной работе реализован датчик случайных чисел с экспоненциальным законом распределения на основе стандартного датчика среды Matlab, имеющего равномерное распределение.

На рисунке 2 показаны гистограмма и функция распределения одной из выборок, полученной с помощью реализованного датчика.

Как видно из рисунка 3, при объеме выборки порядка 10⁴ матожидание и дисперсия сходятся к теоретически расчитанному значению.