Методы рентгенографии

Методы рентгенографии:

Анализ фазового состава:

•  Качественный РФА;

•  Количественный РФА.

        Анализ микроструктуры:

•  Анализ размера блоков мозаики, кристаллитов, микродеформаций и микронапряжений решетки;

•  Анализ простр-х дефектов (упаковки, дислокаций и т.д.)

•  Текстурный анализ (поликристаллов ):

        Анализ атомной кристаллической структуры (рентгеноструктурный анализ):

•  Определение параметров кр.решетки и кристаллографических индексов (индицирование);

•  Уточнение параметров кр.решетки;

•  Определение модели атомной кр. структуры;

•   Уточнение атомной кр. структуры и точечных дефектов.

Абсолютную интегральную интенсивность монохроматического рентгеновского излучения, дифрагированного от плоского толстого однофазного  поликристаллического образца в дифрактометре с фокусировкой по Брэггу-Бретано можно представить как:

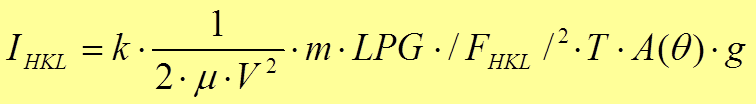       (1)

где К - постоянная, зависящая от физических констант и условий съемки,

m-линейный коэффициент поглощения,

V-объем элементарной ячейки,

LPG-Лоренц-поляризационный и геометрический факторы,

A-угловой фактор поглощения,

T-общий тепловой фактор,

F-структурный фактор,

g-фактор текстурируемости.

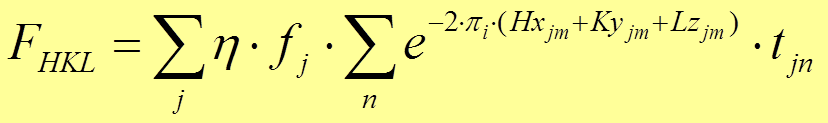     (2)

Где j,n-суммирование по атомам, соответственно, независимой и зависимой части ячейки;

h-коэффициент заполнения кристаллографической позиции;

f_j-атомный фактор рассеяния;

x,y,z-координаты атома в долях ячейки;

H,K,L-кристаллографические индексы;

Угловой фактор поглощения

A=1/(2m)

Тепловые факторы атомов

   t_jm - анизотропный тепловой фактор атома j позиции m

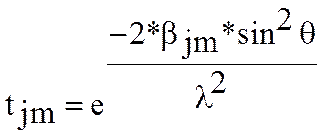                                                    (3)

или изотропный t_j:

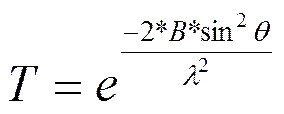                                        (4)                   

Лоренц-поляризационный и геометрический факторы

Для монохроматизированного излучения:

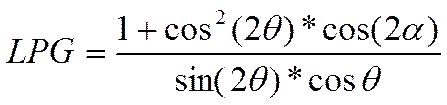                      (5)

где   a-угол отражения от монохроматора.

Факторы текстуры

   поправка на текстуру i-й линии c индексами (hkl):

   Фактор Ритвельда:

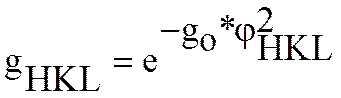                                             (6)

где  g_o -уточняемый параметр текстуры;

  j -угол между нормалью к плоскости (H, K, L) и направлением текстуры.

   или Фактор Марча-Далласа:

ghkl=(G²cos²f_h+ sin²f_h / G)^-3/2       (10)

где f_h – угол между направлением предпочтительной ориентации и вектором обратного пространства R_hkl, соответствующим дифракционной линии с индексами (hkl), G – уточняемый по МНК параметр.

Интегральная интенсивность линии фазы jмногофазного образца

I_hkl,j = K_iI^расч_hkl,jV_j/ m_{j                                                  (*)}

Метод полнопрофильного анализа Ритвельда

Метод полнопрофильного уточнения кристаллических структур многофазных поликристаллических веществ Ритвельда (Rietveld, 1969) [1] дал мощный импульс структурному анализу поликристаллов и является одним из перспективных методов бесстандартного количественного фазового анализа. Метод требует знания структурной модели для каждой фазы анализируемого вещества.  Идея метода состоит в использовании интенсивности рассеяния в каждой точке полного дифракционного профиля дифрактограммы при подгонке рассчитанного профиля к экспериментальному путем варьирования профильных и структурных параметров модели дифрактограммы методом наименьших квадратов.

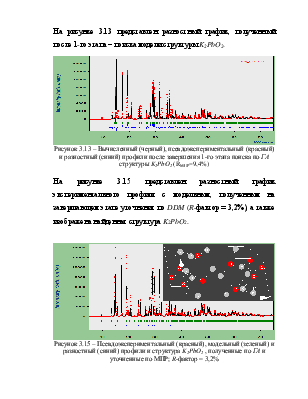
На рисунке 3.13 представлен разностный график, полученный после 1-го этапа – поиска модели структуры K₂PbO₂.

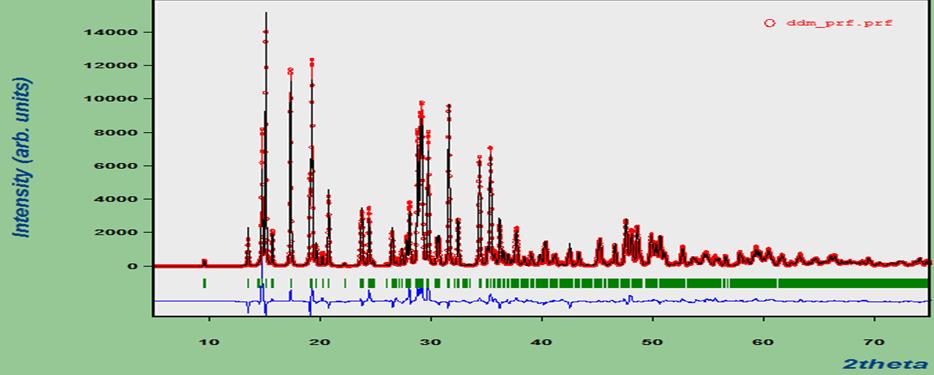
Рисунок 3.13 – Вычисленный (черный), псевдоэкспериментальный (красный) и разностный (синий) профили после завершения 1-го этапа поиска по ГА структуры K₂PbO₂ (R_MПР=9,4%)

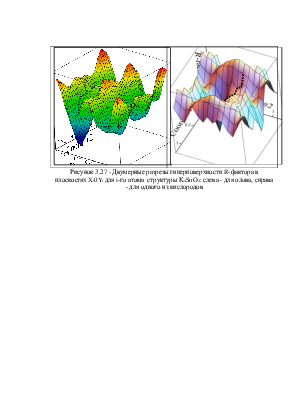
На рисунке 3.15 представлен разностный график экспериментального профиля с модельным, полученным на завершающем этапе уточнения по DDM (R-фактор = 3,2%), а также изображена найденная структура K₂PbO₂.

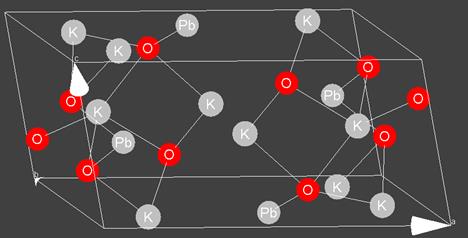
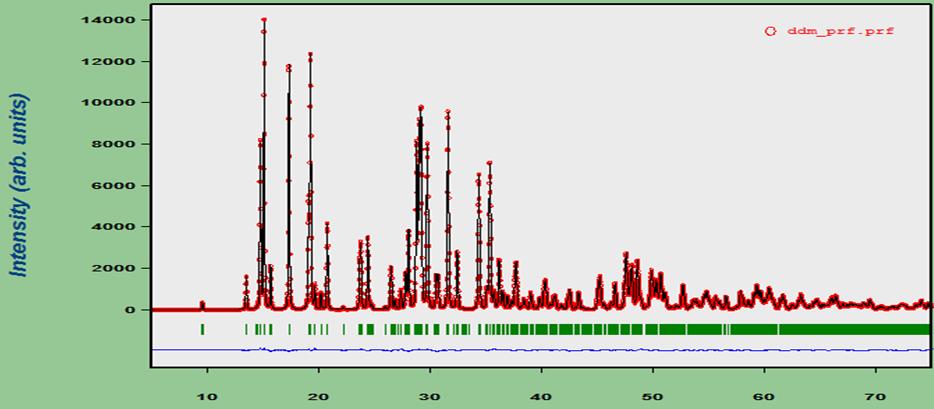
Рисунок 3.15 – Псевдоэкспериментальный (красный), модельный (зеленый) и разностный (синий) профили и структура K₂PbO₂ , полученные по ГА и уточненные по МПР; R-фактор = 3,2%

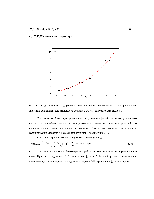
Рисунок 3.27 - Двумерные разрезы гиперповерхности R-фактора в плоскостях X_i0Y_i для i-го атома  структуры K₄SnO₄: слева - для олова, справа - для одного из кислородов

1. Математический аппарат метода Ритвельда

Математическая формулировка метода Ритвельда представляет классический метод наименьших квадратов Ньютона-Гаусса. Метод сводится к минимизации квадрата разности между экспериментальным и рассчитанным профилем с оптимизацией набора профильных и структурных параметров фаз-компонентов анализируемого материала. Формализуя подход, перейдем к следующей математической задаче оптимизации.

Пусть задан некоторый класс параметрических функций Y(P,Q) (многопараметрические функции метода Ритвельда), P– набор их параметров (вектор длины n), Q – независимый аргумент (угол дифракции). По данной дискретной выборке Y^эксп.(Q_j) = {2Q_j, Y_j} значений функции и исходным приближениям ее параметров P₀ требуется найти функцию Y^мод. из класса Y^.(P, Q) (т.е. найти оптимальный набор параметров Р*) такую, чтобы выполнялось условие (1).

Функционал МНК:

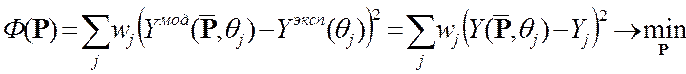(1)

Здесь  и  - интенсивности экспериментальной и вычисленной дифрактограмм в точках  j =1, 2,..., N, образующих профиль рентгенограммы; - вес измерения.

Интенсивность  вычисляется по формуле:

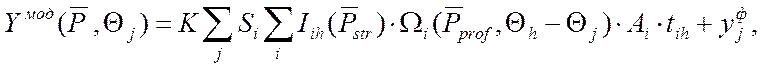           (2)

где К-коэффициент приведения к единой шкале;

- модельная функция фона рентгенограммы;

S_i– масштабный коэффициент для расчетной рентгенограммы фазы i;

 -  вектор параметров,  включающий профильные и структурные параметры фаз,

- интегральная интенсивность рефлекса (hkl) фазы i, определяемая выражением  (*) в п.1 и являющаяся функцией структурных параметров  фазы i;

t_ih – набор мультипликативных поправок на интенсивность рефлекса (hkl)_i фазы i (текстура и т.п.);

- функция профиля i-й фазы для рефлексов (hkl)_i ;

A_i – набор мультипликативных поправок на профиль рефлексов (hkl)  фазы i (асимметрия, и т.п.);

Искомый минимум достигается при некотором P* = P₀+DP.Найдем этоP*.

Необходимое условие минимума функционала:

dF(P*, Qj) / dPi = 0, i = 1, …, N.                                  (3)

Из (1) и (3):

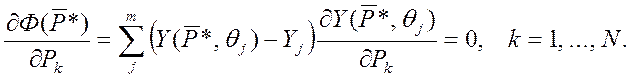                  (4)

Решить систему (4) точно относительно P* не представляется возможным ввиду ее существенной нелинейности. Будем решать приближенно, линеаризуя (4) относительно DP.

Разложим Y(P₀+DP, Qj) по формуле Тейлора:

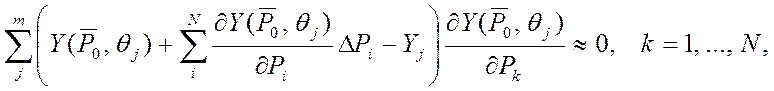
откуда

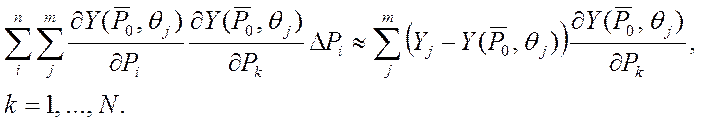         (5)

Получаем систему линейных уравнений (5) от n неизвестных, которую можно решить методом Гаусса. Последовательно находя DP₁ , DP₂ , …  (уточняя значения P₀), будем приближаться к искомому P*.

2. В качестве характеристики «качества» решения применяются один или несколько R-факторов [2].

1.  Профильный (R_p):

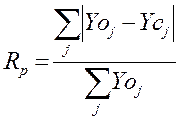,                                                                     (6)

где Yo_j – измеренные в точке θ_j интенсивности, поправленные на фон; Yc_j – расчетные значения.

2.  Взвешенный профильный (R_wp):

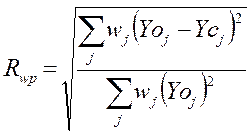,                                                                   (7)

где w_j – весовой коэффициент, отражающий надежность проведенного измерения, обычно равный 1/ Yo_j   [3].

3.  R-фактор по интегральным интенсивностям (R_I – брэгговский) – то же, что и R_p но с использованием интегральных интенсивностей.

4.  Ожидаемый R-фактор (R_exp):

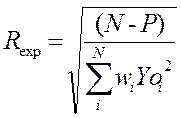,                                                                            (8)

где N – число измерений, P – число параметров.

R_exp – статистически ожидаемый R-фактор, к которому должен приблизится взвешенный профильный фактор.