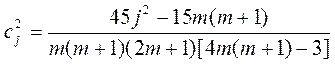Методы рентгенографии, страница 6

                                                          (7)

Фактор соответствия (R-фактор), характеризующий степень различия между наблюдаемой и расчетной дифрактограммами задается выражением:

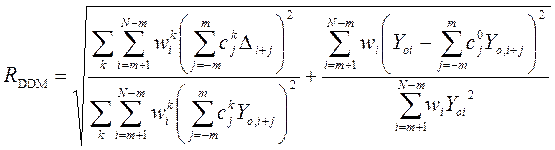                             (8)

R-фактор, вычисляемый в таком виде, наименьшим образом зависит от выбора интервалов свертки [-m, m] и, для дифрактограм с умеренной кривизной фона, сравним с профильным R-фактором R_wp, используемым в методе Ритвельда [4]. Однако, в общем случае, абсолютные величины R_DDM и R_wp не могут сравниваться напрямую при оценке качества уточнения.

Процедура выбора интервала свертки для каждой точки профиля требует особого рассмотрения, поскольку от нее зависит качество и стабильность уточнения параметров модели. С одной стороны, интервалы не должны превышать определенных величин, при которых вычисление профильных производных СГ дает корректные значения. С другой стороны, слишком узкие интервалы свертки делает процедуру оптимизации менее чувствительной к плавным модуляциям разностной кривой. Если рассматривать производную разностной кривой как разность производных расчетной и экспериментальной дифрактограм, можно предложить ряд критериев выбора интервалов свертки, основанных на свойствах процедуры Савитского-Голая. В формализме СГ множители  являются коэффициентами полинома, аппроксимирующего кривую в интервале [-m, m], поэтому в качестве оптимальных можно рассматривать такие интервалы свертки, для которых полином СГ обеспечивает корректную аппроксимацию кривой в пределах экспериментальных ошибок (статистического шума). Наиболее простым является выбор интервала свертки, равного среднему значению полуширины дифракционных максимумов. При этом для большинства точек профиля дифрактограммы вычисление производных будет корректным. Однако, как показывает практическое применение МРП [17,5], более оптимальным является выбор интервалов свертки отдельно для каждой точки экспериментального профиля исходя из его кривизны и величины статистического шума. Процедура заключается в нахождении максимально широкого интервала свертки для каждой точки профиля, при котором среднее отклонение полинома СГ от профильных интенсивностей в точках интервала не превышает величины статистического шума. Данный критерий обеспечивает выбор более узких интервалов для участков профиля с острыми, интенсивными, хорошо разрешенными пиками и более широких интервалов для участков со слабыми, зашумленными и/или перекрывающимися пиками.

Процедура МПР была реализована в пакете компьютерных программ для структурного и фазового анализа поликристаллических веществ [6]. Применение процедуры для дифракционного анализа кристаллических [7,8,19] и мезоструктурированных материалов [9-18] показало, что при малой кривизне фона качество уточнения структурных параметров методом МПР аналогично тому,  что дает применение метода Ритвельда с эмпирической моделью фоновой кривой  [16,17].  При наличии аморфной составляющей и других источников модуляций фона МПР позволяет существенно улучшить качество уточнения по сравнению с методом Ритвельда. Более того, МПР дает возможность определять и уточнять плохо контролируемые параметры, уточнение которых методом Ритвельда может быть невозможным по причине систематических ошибок, возникающих вследствие некорректного моделирования фоновой составляющей. Для ряда веществ была продемонстрирована, в частности, возможность независимого уточнения МПР позиций атомов водорода [17,19].

На рисунке 2 показаны результаты определения и уточнения кристаллической структуры тетразол-нитрогуанидина калия по данным порошковой дифракции [5] методом МПР.

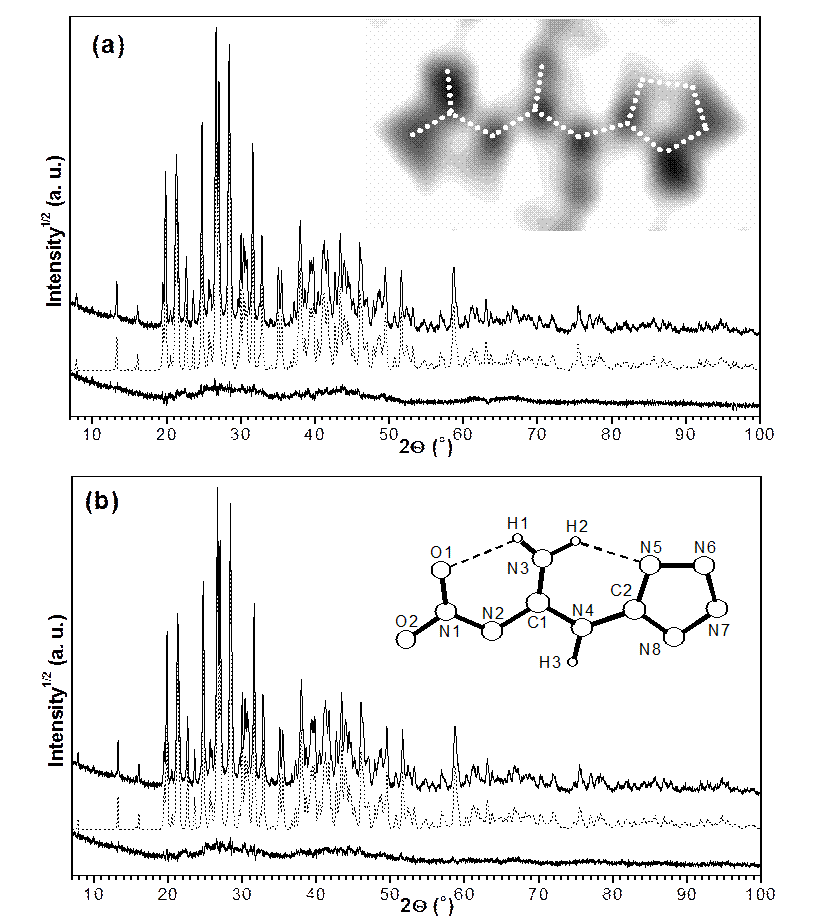
Рисунок 2 - (а) Результаты МПР  декомпозиции рентгенограммы тетразол-нитрогуанидина калия. На вставке показано сечение синтеза Паттерсона, на котором проявляется конформация молекулы. (b) Соответствие между расчетом и экспериментом и уточненное методом МПР расположение атомов структуры

Расположение основных атомов структуры было найдено из синтеза Паттерсона на основе структурных факторов, определенных путем декомпозиции рентгенограммы методом МПР. В результате уточнения структуры и анализа распределения электронной плотности были определены все атомные позиции, включая атомы водорода. При этом координаты атомов водорода уточнялись без каких-либо ограничений на длины и углы связей, что свидетельствует о высокой точности и стабильности метода. Как видно на рис. 2, разностная кривая после уточнения МПР имеет несколько широких максимумов, указывающих на наличии аморфной составляющей в образце. Естественно, что моделирование такой сложной кривой при использовании метода Ритвельда составляет существенную проблему.

2.2. Реализация метода в компьютерной программе DDM

Метод минимизации производной разности реализован в компьютерной программе полнопрофильного дифракционного анализа DDM (Derivative Difference Minimization). Данная программа позволяет уточнять кристаллические структуры и проводить количественный фазовый анализ по порошковым дифракционным данным с использованием метода МПР, а также, для сравнения по желанию пользователя,  метода Ритвельда, встроенного для этой цели в DDM.

Интенсивности профиля дифрактограммы Yc_i рассчитываются путем суммирования формы  дифракционных максимумов всех кристаллических компонент (фаз) образца и необязательной кривой фона Yb_i:

Yc_i = S_p s_p {S_k [ |F_k|² f(2q_i - 2q_k) L_k P_k Sa ]}_p + Yb_i,

где s_p – масштабный коэффициент фазы, F_k – структурный фактор,  f – функция формы пиков, L_k – фактор Лоренца и поляризации, P_k – функция преимущественной ориентации, Sa – коррекция на поглощение (включая микропоглощение) и толщину образца.

Функция формы пиков имеет несколько вариантов:

(0)         exp[-C_o(2q_i - 2q_k)² /H_k²] ÖC_o /H_kÖp                         Gaussian

(1)         [1+C₁(2q_i - 2q_k)² /H_k²]^-1 ÖC₁ /pH_k                            Lorentzian

(2)         [1+C₂(2q_i - 2q_k)² /H_k²]^-2 2ÖC₂ /pH_k                          Lorentzian Mod 1

(3)         [1+C₃(2q_i - 2q_k)² /H_k²]^-1.5 ÖC₃ /2H_k                          Lorentzian Mod 2

(5)         nL + (1 - n)G,  n = NA + NB*2q                             pseudo-Voigt

(6)         (C₄/H_k) [1 + 4(2^1/m - 1) (2q_i - 2q_k)² /H_k²]^-m               Pearson VII

m = NA + NB/2q + NC/(2q)²

             H_k = [(U + Aniso₂)tan²q +V tanq +W + (Z + Aniso₁Fder)/cos²q ]^1/2