В [29] метод Ритвельда применен для количественного определения кристаллических и аморфных фаз в керамических материалах. Шесть кристаллических фаз были проанализированы с этой целью в почти полностью (>95% масс.) аморфном материале после добавления известного количества внутреннего стандарта (TiO2). Количественные исследования корректировались с учетом эффекта микропоглощения, размера зерна и коэффициентов поглощения. После идентификации кристаллических фаз, представленных в образце, массовая доля обнаруженных фаз была вычислена обработкой профиля методом Ритвельда с использованием программного обеспечения FullProf. Поскольку материал главным образом аморфный и существенен фон, то для его учета был посчитан полином шестого порядка для его удаления.
Эти исследования продемонстрировали возможность использования метода Ритвельда для определения содержания кристаллических фаз в преобладающе аморфных (>95% веса) материалах. Поправки на микропоглощение привели к завышению конечных результатов по массовым долям для кристаллических фаз. Несмотря на небольшое содержание кристаллических фаз, обработка профиля показала существенные структурные изменения для одной из фаз образца CaMoO4. Эти данные были подтверждены электронным микроисследованием и химическим анализом.
В [30] описывается новый, альтернативный методу Ритвельда, объединенный подход к анализу порошковых материалов, использующий весь профиль рентгенограммы и реализованный в коммерческой программе SNAP-1D. Подход включает предварительную обработку данных, непараметрические статистические процедуры, и процедуру разделения линий для более точного извлечения количественной информации о фазах в смеси. Данный подход не требует знания кристаллических структур фаз так как используются эталонные профили из БД и информация о составе элементарной ячейки. Его точность, определенная на материалах Round Robin по КРФА, составляет 1-5% в зависимости от качества данных. Предел чувствительности для него около 5%. Общее время всех вычислений на ПК составляет меньше 1 минуты.
2. Метод минимизации производной разности
Метод минимизации производной разности (МПР) [2] был создан недавно как альтернатива МНК-процедуре оптимизации невязок между расчетной и экспериментальной дифрактограммами, используемой в методе Ритвельда. Он позволяет проводить полнопрофильный анализ кристаллических компонент порошковой дифрактограммы независимо от кривой фона, которая может содержать различные компоненты аморфного рассеяния и другие паразитные составляющие. Независимость от фона не требует параметрического моделирования кривой фона, как это реализовано в методе Ритвельда, и, следовательно, снижает размерность оптимизационной задачи генетического алгоритма при использовании МПР в качестве метода локальной оптимизации и уточнения профильных и структурных параметров на 2-м уровне ГА. Рассмотрим основы и программную реализацию метода МПР, и его адаптацию, выполненную для использования МПР в генетическом алгоритме.
2.1. Описание метода минимизации производной разности
В методе МПР кривая разности между расчетным и экспериментальным профилем дифрактограммы рассматривается в качестве аппроксимирующей линии фона, которая предполагается плавно меняющейся функцией угла дифракции. В отличие от МНК-процедуры, используемой в методе Ритвельда, в МПР оптимизация структурных, микроструктурных и других параметров, включенных в модель дифрактограммы, производится путем минимизации кривизны и осцилляций разностного профиля, а не абсолютных значений невязок. При большом различии между расчетом и экспериментом кривизна и осцилляции разностного профиля большие, по мере улучшения соответствия между расчетом и экспериментом кривизна и осцилляции разности уменьшаются (рисунок 1). При таком подходе необходимость включения в модель линии фона отсутствует, что позволяет не только облегчить процедуру полнопрофильного анализа, но и минимизировать влияние систематических ошибок, возникающих вследствие некорректного моделирования фоновой составляющей дифрактограммы.
В качестве минимизируемого функционала используется сумма квадратов производных разностного профиля в каждой точке дифрактограммы:
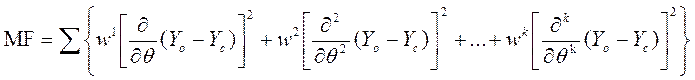(1)
где Yo и Yc – интенсивности экспериментального и расчетного профиля, q – угол дифракции, w – весовой фактор, а суммирование проводится по всем точкам дифракционного профиля. Используя формализм Савитского-Голая (СГ) [3] для вычисления производных минимизируемый функционал может быть представлен в виде:
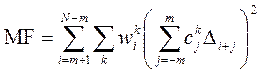(2)
где 
– коэффициенты СГ производной
порядка k для интервала
свертки профиля [-m, m],
N – количество точек профиля, D - профильная разность (D = Yo - Yc).
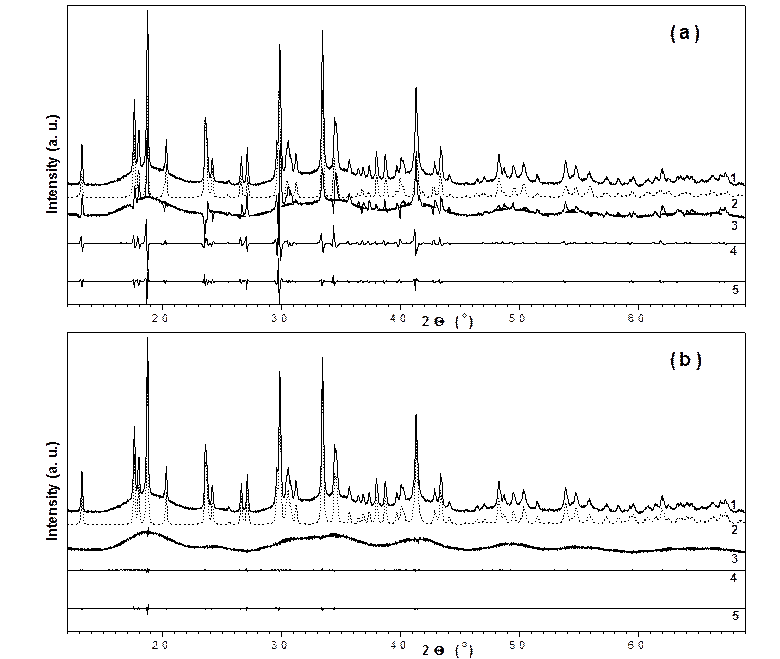
Рисунок 1 - Результат минимизации производной разности для модельной рентгенограммы (1) со сложной кривизной фона. Показаны расчетный (2) и разностный (3) профили, а также первая (4) и вторая (5) производная разности до (a) и после МПР (b)
Уточнение варьируемых параметров модели дифрактограммы vr производится путем решения ортогональных уравнений, соответствующих минимуму функционала (2):
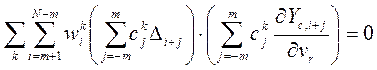(3)
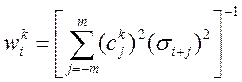(4)
где s i – среднеквадратичная ошибка в измерении профильной интенсивности Ioi. Весовой фактор wik представляет обратную величину ошибки в вычислении производной порядка k в i-й точке профиля. Среднеквадратичная ошибка в определении варьируемых параметров модели определяется как:
si = [Aii-1MF/ (N - P + C)]1/2 (5)
где Aii-1 – диагональные элементы инвертированной нормальной матрицы, N – количество экспериментальных точек, P – количество уточняемых параметров, а C – общее количество ограничений, накладываемых на уточняемую модель.
Для практического использование количество производных и степень полинома
Савитского-Голая необходимо ограничить определенными значениями. Тестовые
прогоны процедуры показали, что приемлемое качество и точность уточнения
достигается при использовании первой и второй производных для полинома СГ
второй степени. Коэффициенты для 1-й и
2-й производных с интервалом свертки [-m, m] вычисляются
следующим образом:
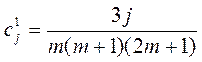(6)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.