Методы рентгенографии, страница 4

Шаг 5. Выполняется циклическая процедура обработки. По умолчанию уточняемые параметры: сдвиг нуля и фоновые коэффициенты (глобальные параметры) и, для каждой фазы, масштабный фактор, параметры ячейки, FWHM (полуширина пика), асимметрия:

Пирсон VII:

Для других функций:

где а – параметр ассиметрии.

               Учет поправки на абсорбцию выполняется в зависимости от способа запрессовки образца [22]:

1. По Дебаю – Шерреру (цилиндрический образец):

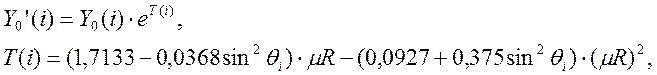
где R – радиус цилиндра. Значение µR  задается пользователем.

2. По Брегу – Брентано (плоский образец):

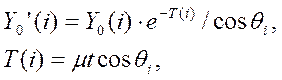
где t – толщина образца. Значение µt задается пользователем.

               Если учитывается РО (предпочтительная ориентация частиц), то фактор РО может  уточняться с помощью функции March-Dollase [23,24]:

                                                              (40)

α – угол между направлением предпочтительной ориентации и вектором h.

               Существенные эффекты предпочтительной ориентации, вероятно, будут характеризованы наименьшей величиной параметра G. Величины G – обычно недооцениваются процедурой. Максимально может быть задано три направления РО, тогда общая поправка для каждого вектора h:

где f_i – предпочтительная ориентация частиц в i-ом направлении, с ограничением:

               Анизотропное уширение пиков учитывается с помощью эмпирической функции, предложенной Ле Бэйлом (1997) [25] для моделирования изменений FWHM и пиковой формы:

H_h = [W_h + V_h tgθ_h  + U_h tg²θ_h]^1/2,

и

W_h=d²_h(W₁₁h²a^*2+W₂₂k²b^*2+W₃₃l²c^*2+2W₁₂hka*b*+2W₁₃hla*c*+2W₂₃klb*c*).

             Аналогичные выражения получаются для V_h, U_h и для смешенных параметров функций Пирсона и  псевдо-войта.     

             Программа останавливается когда

для всех уточняемых параметров; ∆x_j и δ_j - изменение и предполагаемое стандартное отклонение параметра j, соответственно и ε = 0.3 (по умолчанию).

             Стратегия обработки следующая: уточняемые параметры вовлечены в минимизацию наименьших квадратов; применяются числовые ограничения  параметров и динамические вариации затухающих факторов; уточнения χ² проверяются цикл за циклом, чтобы  контролировать конвергенцию; параметры, отклоняющиеся от дозволенных диапазонов, блокируются. Как только достигается схождение, вычисляется содержание фаз по формуле (34).

              Чтобы учесть в расчете возможные микроабсорбционные эффекты, необходимо знание среднего значения радиуса частицы каждой фазы. Величины автоматически исправляются согласно теории Брендлея [26].

            Содержание аморфной фазы может быть получено по следующему уравнению:

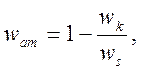
где w_k – количество добавки, w_s – количество стандарта, вычисленное по методу Ритвельда.

            Тогда содержание кристаллической фазы в смеси с учетом внутреннего стандарта:

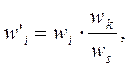
           Отсюда, содержание каждой кристаллической и аморфной фазы вычисляется по следующему уравнению:

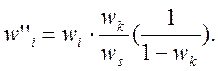
          Следует отметить возможность автоматической процедуры для нахождения направлений предпочтительных ориентаций, которая осуществляется в Quanto после запроса пользователем.

            Литературный обзор научных статей, посвященных  инновациям в области разработок метода Ритвельда, показал, что одно из актуальных направлений заключается в стремлении авторов повысить точность и найти универсальный способ по определению аморфной составляющей в различных объектах исследования. Ниже приводится анализ некоторых таких попыток.                

        Рядом  авторов, например, предпринимались попытки по количественному определению фаз в системах, в которых фаза с кристаллической структурой как бы «вложена» в аморфную матрицу, то есть это практически полностью аморфные системы. Например, КРФА основанный на теории Ритвельда был применен к кристаллическим полимерам [34,37]. В [35,36] также применен метод Ритвельда и предложено рассматривать аморфную фазу как нанокристаллическую, то есть фазу с очень короткой последовательностью. В другом подходе [29] для оценки содержания кристаллической фазы   в частично аморфных соединениях использовался дифракционный профиль образца, в котором аморфные и фоновые вклады вычитались из рентгенограммы (но при этом в  образец было необходимо добавлять аналитический стандарт). Однако все вышеперечисленные подходы наткнулись на серьезную проблему, а именно построение такой структурной модели, которая бы учитывала аморфную полимерную матрицу и поглощенную ею воду.  К тому же, метод Ритвельда требует задания кристаллоструктурных данных для каждой фазы, которые полностью неизвестны для сложных структур органического происхождения.

             С помощью программы GSAS [31] и добавлением известного количества внутреннего стандарта [28] было определено содержание аморфной фазы в силикате кальция, C3S (Ca₃SiO₅), являющегося главным компонентом Портлендского цемента, Из нескольких стандартов (α-Al₂O₃, MgO, TiO₂, SiO₂, CaCO₃) α-Al₂O₃ дал наилучшие результаты. С его помощью содержание аморфной фазы определено по балансу с точностью до 1 масс. %. Пробоподготовка и сам анализ были тщательно отработаны, для минимизирования систематической ошибки. Анализ образцов, содержащих фазы с сильным эффектом предпочтительной ориентации частиц привел к очень высоким ошибкам в определении аморфной составляющей. Для  оценки влияния эффекта микропоглощения по методу Бриндлея были изучены образцы, фазы которых имеют различные  коэффициенты поглощения (LaGa_0,87Mg_0,13O_2,9 и Al₂O₃; LaGa_0,87Mg_0,13O_2,9 и TiO₂).  Размер частиц определялся с помощью электронного микроскопа Jeol SM 840.    Значение R_F - фактора для C3S выше, чем таковые для аналогичных составов, потому что эта фаза имеет сложную сверхструктуру с множеством пиков низкой интенсивности, определение которых затруднено. Определение содержания аморфной фазы для этой системы очень важно, потому что она имеет огромное влияние на кинетику гидратации. Кроме того, процедура, описанная в этой работе, может применяться для  определения количества аморфного C-S-H геля при гидратации кальциевых силикатов.