Исходными данными метода Ритвельда являются порошковая дифрактограмма, результаты индицирования (параметры решетки и пространственные группы симметрии фаз), структурные модели фаз и исходные приближения основных параметров профиля. Структурный анализ обычно проводится в две стадии:
а) уточнение профиля без структурных данных [5];
б) уточнение профиля и структурных моделей фаз.
В заключение может быть выполнен КРФА, как описано выше в разделе 3.5.
Для контроля за процессом подгонки применяют разностные графики, которые строятся путем вычитания экспериментальной дифрактограммы из расчетной.
Итерационный метод Ритвельда имеет три существенные проблемы.
1). При недостаточно точных начальных приближениях P0 и большом числе параметров n система (4) расходится либо устойчиво попадает в локальный минимум. Чем больше n, тем точнее требуютсяP0 .
2). Сходимость и точность метода существенно зависит от качества моделирования формы линий и фоновой составляющей. Хорошими аппроксимациями формы линий признаны асимметричные варианты распределений Пирсона VII и псевдо-Войгта, а фона – некоторыми полиномами [4]. Тем не менее, анализ материалов с заметным количеством аморфной фазы, дефектными или структурно разупорядоченными фазами и сложной микроструктурой представляет существенные трудности.
3) Метод не достаточно автоматизирован. На практике его использование трудоемко и требует длительного подбора «хороших» начальных приближений для части основных параметров и постепенного вовлечения в уточнение всех оставшихся.
6.2. Связи между уточняемыми параметрами и структурные ограничения
Кристаллическая структура описывается совокупностью параметров, которые определяют положения атомов, их перемещения и вероятность того, что каждый атом занимает свою позицию. Это параметры координат атомов внутри ячейки, атомные смещения или тепловые параметры, и факторы оккупации. Дополнительный набор параметров описывает порошковый дифракционный профиль через параметры решетки, профильные параметры и коэффициенты фона, текстуры, абсорбции и других эффектов. Эти параметры могут непосредственно влиять на другие параметры через пространственную группу симметрии или через отношения, которые может фиксировать экспериментатор для уменьшения размерности оптимизационной задачи. Такие отношения могут быть описаны в уточнении как «связи», которые связывают изменения в параметрах Dpi и могут быть представлены как:
![]() (9)
(9)
где kij - это элементы разряженой квадратной матрицы, которая связывают группы параметров в небольшой набор тех, которые действительно уточняются. Это сокращение числа частных производных представляется так:
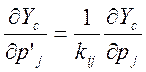 (10)
(10)
В простейшей форме эти связи могут использоваться для атомных координат в специальных позициях (например, позиция x,x,x в кубической пространственной группе), где есть особые отношения между отдельными атомными координатами, а также между отдельными параметрами анизотропных температурных колебаний (например, когда U11 = U22 = U33 и U12 = U13 = U23 для кубических позиций в x,x,x).
Для больших структур число параметров, требуемых для её описания, больше, чем может быть определено из дифракционных данных, полученных в одном эксперименте. Такая ситуация может быть разрешена введением дополнительной информации в задачу уточнения. Очень часто некоторые части структуры имеют хорошо известные стереохимические свойства. Например, может иметься одна (или несколько) фенильных (-C6H5) групп, которые могут быть приняты плоскими с равномерными длинами связей C-C и C-H. Эта информация может быть получена при помощи различных методов анализа. Один из путей – это описание молекулярного фрагмента как «твердого тела», которое имеет свою ориентацию и положение в кристаллической структуре. В начале этот структурный фрагмент может быть описан в локальной системе Декартовых координат заданием списка координат x,y,z его атомов, который затем, в процессе уточнения положения фрагмента как целого, может перемещаться последовательной трансляцией атомов из Декартового начала координат.
Альтерантивный метод получения дополнительной информации для уточнения структуры может включать оценки ошибок различных стереохимических характеристик. Эти дополнительные наблюдения вводят дополнительные условия в функцию минимизации (1) по методу наименьших квадратов:
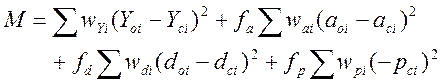 (11)
(11)
Такими условиями являются: a – углы связей, d – длины связей, и p – производные от лучшей плоскости; весовые коэффициенты f выбираются для баланса различных вкладов и предотвращения любого избыточного влияния любым блоком условий. Отдельные веса наблюдений определяются из стандартной неопределенности, связанной с каждым наблюдением. В отличие от жесткого задания фрагментов твердого тела, использование вероятностных ограничений не приводит к уменьшению числа параметров, использующихся для описания кристаллической структуры, но оно включает дополнительную стереохимическую информацию, позволяющую проводить более полное уточнение дифракционного профиля и, соответственно, структуры.
Описанные подходы позволяют выполнять уточнение весьма сложных кристаллических структур, например, белков, представленных чрезвычайно большим числом атомных позиций. В частности, хорошо изученная тетрагональная кристаллическая стрктура белка куриного яйца лизозима имеет 1001 неводородный атом в одной белковой молекуле; другие 100 представляют или молекулы воды или ионы соли. Имеется более 3000 атомных координат x,y,z. Однако уточнение по Ритвельду этой структуры из данных порошковой дифракции [6] было получено с помощью набора ограничений (11), включающих характерные стереохимические характеристики фрагментов, определенные из результатов исследования монокристаллов белковых структур высокого разрешения и их маленьких пептидов.
6.3. Оценка ошибки количественного анализа по методу Ритвельда
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.