Приложение
КРАСНОЯРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Инженерно-физический факультет
Кафедра высокоэнергетических процессов обработки материалов
КУРСОВАЯ РАБОТА
по дисциплине
«Физические основы генерации лазерного излучения»
Вариант № 1
Студента ИФФ, 3 курс,
гр. ИФ 10-1, подпись А. В. Иванов
Руководитель
профессор каф. ВЭПОМ подпись В. П. Тимофеев
Красноярск 2003
Дана усиливающая среда,
представляющая собой газ двухуровневых атомов (рис.1), приведенный в состояние
инверсной заселенности с ![]() . Концентрация атомов среды
. Концентрация атомов среды ![]() , длина среды
, длина среды ![]() . Форма спектральной линии атомного
перехода обусловлена ударным уширением с шириной линии
. Форма спектральной линии атомного
перехода обусловлена ударным уширением с шириной линии ![]() . Длина волны перехода
. Длина волны перехода ![]() , его сила осциллятора
, его сила осциллятора ![]() . На вход среды поступает слабый
монохроматический сигнал с резонансной атомному переходу частотой и с
интенсивностью
. На вход среды поступает слабый
монохроматический сигнал с резонансной атомному переходу частотой и с
интенсивностью ![]() .
Уровни атомного перехода являются невырожденными. Показатель нерезонансных
потерь среды
.
Уровни атомного перехода являются невырожденными. Показатель нерезонансных
потерь среды ![]() .
.
Определить:
1. Коэффициенты Эйнштейна B12, B21, A12.
2. Интенсивность насыщения среды Is.
3. Показатель
линейного усиления среды ![]() .
.
4. Зависимость
выходной интенсивности сигнала ![]() от
длины среды
от
длины среды ![]() , считая
, считая ![]() переменной величиной. Построить
график этой зависимости и дать ее анализ. Указать область значений параметров,
при которых величина
переменной величиной. Построить
график этой зависимости и дать ее анализ. Указать область значений параметров,
при которых величина ![]() будет
оптимальной.
будет
оптимальной.
5. Коэффициент усиления среды.
6. Сделать выводы в целом по заданию №1.
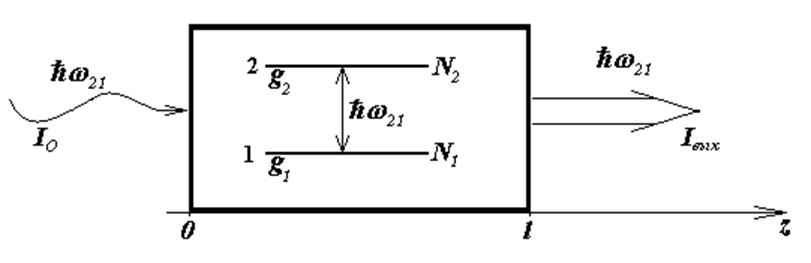
Рис. 1
1. Определение коэффициентов Эйнштейна
Согласно формулам (27) и (28) работы [1], коэффициенты Эйнштейна связаны между собой соотношениями
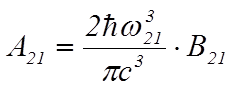 ,
, ![]() , (1)
, (1)
где ![]() и
и ![]() – статистические веса (факторы
вырождения) уровней 2 и 1 соответственно (Рис. 1),
– статистические веса (факторы
вырождения) уровней 2 и 1 соответственно (Рис. 1), ![]() – постоянная Планка, c – скорость света в вакууме,
– постоянная Планка, c – скорость света в вакууме, ![]() – циклическая частота перехода 2 ® 1. Поскольку по условию задания уровни
не вырожденны, то следует положить
– циклическая частота перехода 2 ® 1. Поскольку по условию задания уровни
не вырожденны, то следует положить ![]() .
.
Поступим следующим образом: вначале определим коэффициент ![]() , а через него - коэффициенты B21 и B12.
Согласно работе [4],
, а через него - коэффициенты B21 и B12.
Согласно работе [4],
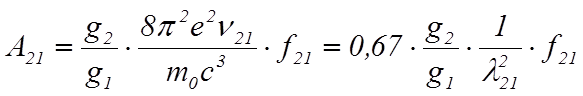 , (2)
, (2)
где e
– заряд электрона, m0 – его масса
покоя, 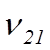 и
и ![]() – соответственно частота и длина
волны перехода 2 ® 1,
– соответственно частота и длина
волны перехода 2 ® 1, ![]() – сила осциллятора этого
перехода. Формула (2) записана в системе СГСЭ, поэтому
– сила осциллятора этого
перехода. Формула (2) записана в системе СГСЭ, поэтому ![]() должна выражаться в сантиметрах.
Подставляя в (2) значения величин, получаем
должна выражаться в сантиметрах.
Подставляя в (2) значения величин, получаем
![]()
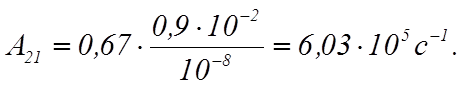 (3)
(3)
Из (1) вычисляем B21 и B12:
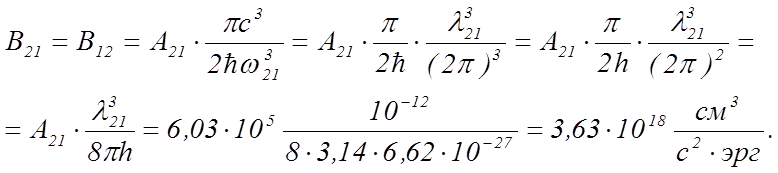 (4)
(4)
2. Определение интенсивности насыщения среды
Согласно формуле (114) работы [1], интенсивность насыщение системы двухуровневых атомов при точном резонансе и в стационарном случае
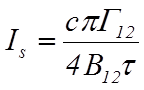 , (5)
, (5)
где ![]() – однородная ширина спектральной
линии перехода,
– однородная ширина спектральной
линии перехода, 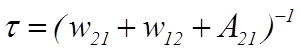 – время
релаксации системы,
– время
релаксации системы, ![]() и
и ![]() – скорости безизлучательной
релаксации системы соответственно сверху вниз и снизу вверх. Поскольку в данном
случае рассматриваемый переход имеет длину волны, лежащую в оптическом
диапазоне, т. е.
– скорости безизлучательной
релаксации системы соответственно сверху вниз и снизу вверх. Поскольку в данном
случае рассматриваемый переход имеет длину волны, лежащую в оптическом
диапазоне, т. е. ![]() , где
, где ![]() – постоянная Больцмана, а Т –
температура газа, то слагаемым
– постоянная Больцмана, а Т –
температура газа, то слагаемым ![]() можно
пренебречь. Кроме того, по условию задачи форма спектральной линии перехода
определяется ударным уширением, следовательно скорость безызлучательной
релаксации системы сверху вниз
можно
пренебречь. Кроме того, по условию задачи форма спектральной линии перехода
определяется ударным уширением, следовательно скорость безызлучательной
релаксации системы сверху вниз ![]() будет
определяться временем свободного пробега атомов и будет превышать скорость
спонтанного распада верхнего уровня, т.е.
будет
определяться временем свободного пробега атомов и будет превышать скорость
спонтанного распада верхнего уровня, т.е. ![]() >>
>>![]() . Таким образом, можно
положить
. Таким образом, можно
положить 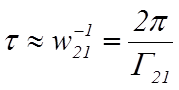 и записать
и записать
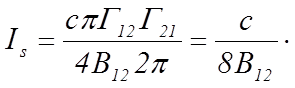
![]() . (6)
. (6)
Чтобы выразить ![]() в обратных сантиметрах, следует в
(6) положить
в обратных сантиметрах, следует в
(6) положить ![]() , где
, где ![]() имеет размерность см-1.
Тогда
имеет размерность см-1.
Тогда
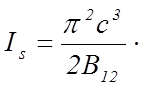
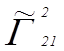
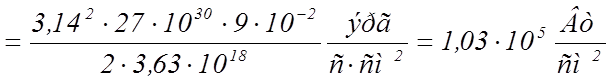 . (7)
. (7)
3. Определение показателя линейного усиления среды
В качестве исходного выражения, описывающего показатель линейного усиления, можно воспользоваться формулой (120) работы [1]:
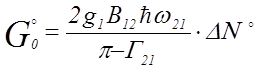 , (8)
, (8)
где ![]() – инверсия среды в начальный момент
времени (до воздействия излучения). Переписывая эту формулу в удобный для
расчета вид, получаем
– инверсия среды в начальный момент
времени (до воздействия излучения). Переписывая эту формулу в удобный для
расчета вид, получаем
![]()
![]()
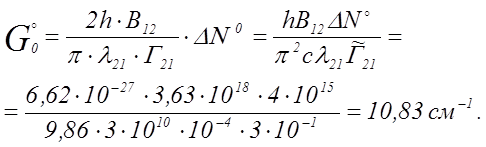 (9)
(9)
4. Определение зависимости выходной интенсивности сигнала от длины усилителя
В данном случае необходимо воспользоваться решением (139), приведенным в работе [1]:
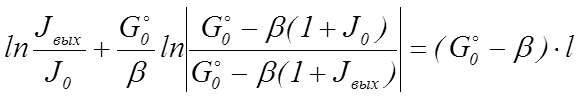 , (10)
, (10)
где ![]() и
и ![]() – значения отношения
– значения отношения ![]() соответственно на входе и на выходе
усилителя. Решение (10) представлено в трансцендентной форме, следовательно,
выразить из него
соответственно на входе и на выходе
усилителя. Решение (10) представлено в трансцендентной форме, следовательно,
выразить из него ![]() в явном виде не
представляется возможным. Поэтому для нахождения зависимости
в явном виде не
представляется возможным. Поэтому для нахождения зависимости ![]() необходимо воспользоваться численным
расчетом на компьютере. Используя, например, пакет программ MatLab,
можно составить следующую программу этого расчёта:
необходимо воспользоваться численным
расчетом на компьютере. Используя, например, пакет программ MatLab,
можно составить следующую программу этого расчёта:
% Определение зависимости выходной интенсивности сигнала
% от длины усилителя
Go=1.083*10^1; Is=1.03*10^5; B=10^(-4);
%-- На нашем промежутке --%
Iv=10^(-4):51400:5.14*(10^7);
Io(1:length(Iv))=10^(-10);
Jv=Iv./Is; Jo=Io./Is;
L=(log(Jv./Jo)+(Go./B).*log(abs((Go-B.*(1+Jo))./(Go-...
B.*(1+Jv)))))./(Go-B);
plot(L,Jv)
grid on; xlabel('L'); ylabel('Jv');
%-- в начале --%
Iv=10^(-2):(10^2):1.115*10^(4);
Io(1:length(Iv))=10^(-10);
Jv=Iv./Is; Jo=Io./Is;
L=(log(Jv./Jo)+(Go./B).*log(abs((Go-B.*(1+Jo))./(Go-...
B.*(1+Jv)))))./(Go-B);
plot(L,Jv)
grid on; xlabel('L'); ylabel('Jv');
%-- до насыщения --%
Iv=10^(-2):(10^5):1.115*10^(10);
Io(1:length(Iv))=10^(-10);
Jv=Iv./Is; Jo=Io./Is;
L=(log(Jv./Jo)+(Go./B).*log(abs((Go-B.*(1+Jo))./(Go-...
B.*(1+Jv)))))./(Go-B);
plot(L,Jv)
grid on; xlabel('L'); ylabel('Jv');
Результат расчета представлен на рис. 2 и
рис. 3 в виде графиков ![]() :
:
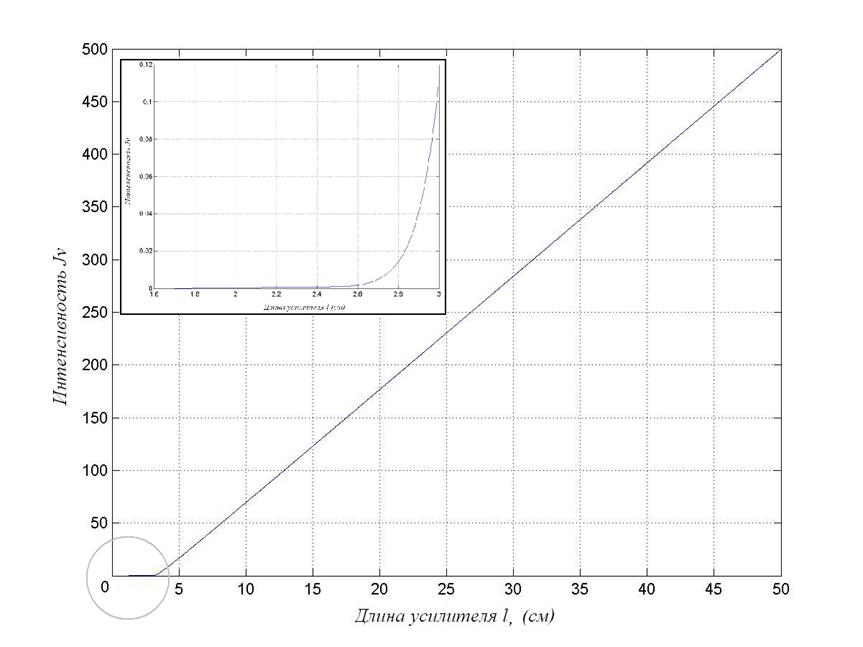
Рис. 2. Зависимость интенсивности выходного сигнала усилителя от его длины
Кривая ![]() переходит
в режим насыщения при
переходит
в режим насыщения при ![]() см.
Это показано на рис. 3.
см.
Это показано на рис. 3.
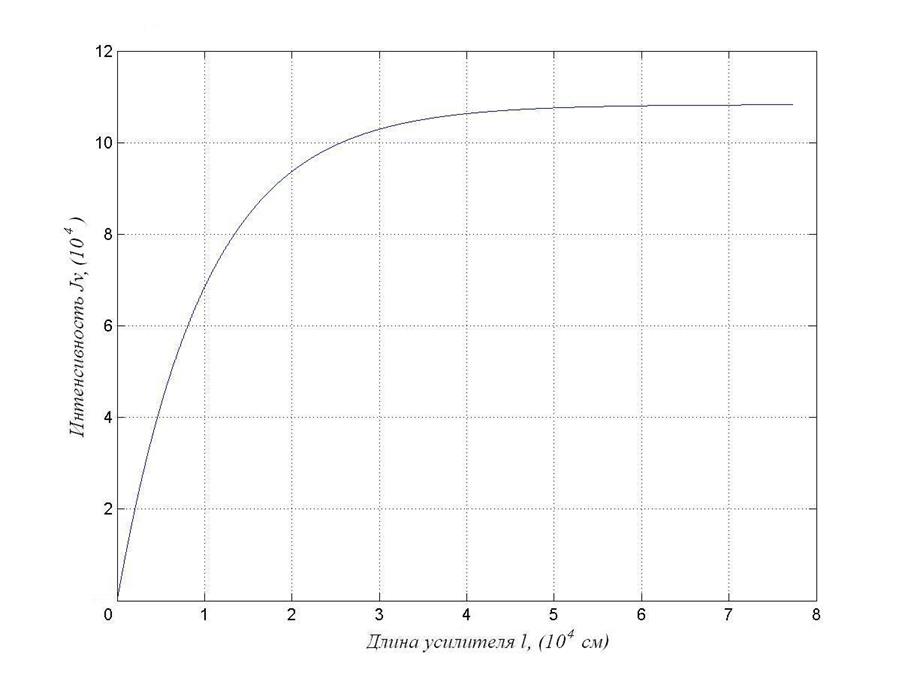
Рис. 3. Зависимость интенсивности выходного сигнала усилителя от его длины
5. Определение коэффициента усиления среды
Коэффициент усиления среды определяется следующим выражением:
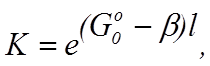 (11)
(11)
где ![]() – показатель
линейного усиления,
– показатель
линейного усиления, ![]() – нерезонансные
потери среды,
– нерезонансные
потери среды, ![]() – длина
резонатора. Подставляя значения соответствующих величин, получаем
– длина
резонатора. Подставляя значения соответствующих величин, получаем
![]() (12)
(12)
6. Выводы по заданию №1
При выполнении задания №1 получены следующие результаты:
1. В разделе 1 определены
коэффициенты Эйнштейна: ![]() ;
; ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.