Решение заданий на усиление излучения, лазерную генерацию и лазерные резонаторы, страница 4

Таким образом, если уменьшить длину активной среды лазера до 21,8 см, а коэффициент отражения выходного зеркала резонатора увеличить до 0,68, то лазер будет работать в режиме максимального КПД, а интенсивность выходного излучения при этом будет наибольшей и равной 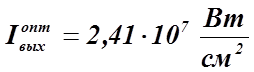. Если в условиях максимального КПД требуется увеличить I_вых, т. е. сделать , то для этого потребуется заменить активную среду на другую, с более подходящими значениями G_o, b, G₂₁, ¦₂₁. Другими словами, при использовании в лазере активной среды, параметры которой заданы вариантом № 1, интенсивность его выходного излучения, генерируемого в условиях максимального КПД, не может быть увеличена свыше .

Задание №3. Лазерные резонаторы

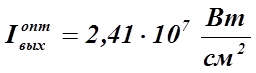Резонатор лазера длиной L=50 см образован двумя сферическими зеркалами круглой формы. Радиусы кривизны отражающих поверхностей зеркал равны r₁=¥ и r₂=105 см, коэффициенты их отражения R₁=0,3 и R₂=1 соответственно, а диаметры одинаковы и равны 0,8 см. Резонатор съюстирован с точностью до угла g=5×10^-3 градуса.

Определить:

1. Число Френеля для данного резонатора.

2. Коэффициент полных потерь  излучения в резонаторе на частоте основной поперечной моды. При этом считать, что основной вклад в них дают потери на пропускание зеркал, потери из-за неточности юстировки резонатора и дифракционные потери.

3. Добротность резонатора на частоте основной поперечной моды, время жизни фотона в этой моде и ширину резонансной кривой резонатора.

4. Является ли данный резонатор устойчивым.

5. Частотный спектр лазерного излучения.

6. Пространственные характеристики лазерного излучения.

7. Сделать выводы в целом по заданию №3.

Решение

1.  Определение числа Френеля

Поскольку диаметры зеркал резонатора одинаковы, то для вычисления числа Френеля необходимо воспользоваться формулой (10) работы [2]:

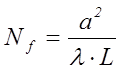                                                           ,                                                                 (26)

где a – радиус зеркал. Подставляя значение входящих в формулу (26) величин, получаем

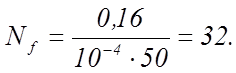                                                                                                                    (27)

2.  Определение коэффициента потерь

Согласно условию полные потери в основном определяются потерями на пропускание зеркал, потерями из-за неточности юстировки резонатора и дифракционными потерями. Каждому виду потерь соответствует свой коэффициент потерь. Следовательно, коэффициент полных потерь будет суммой этих коэффициентов:

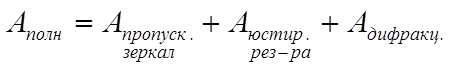                                                                                                     (28)

Для вычисления первого слагаемого в (28) можно воспользоваться формулой (4), второго - формулой (5), а третьего - формулой (6) работы[2]. Тогда

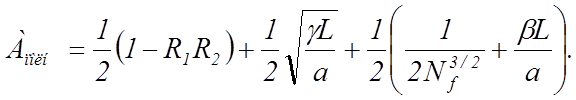                                                                                         (29)

Подставляя в (29) значения соответствующих величин, получаем (a=0,4 см)

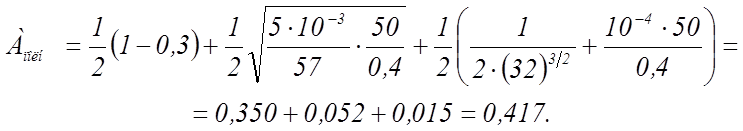                                                                 (30)

3.  Определение добротности резонатора

Известно, что добротность резонатора определяется величиной потерь излучения, распространяющегося внутри него. Поскольку требуется определить добротность для основной поперечной моды, то можно использовать для этого вычисленный выше коэффициент полных потерь (30). В этом случае, согласно работе [2], добротность можно записать формулой (26)

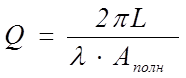                                                       .                                                                 (31)

Подставляя в (31) значения соответствующих величин, получаем

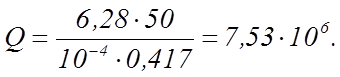                                                                                                             (32)

Время жизни фотона в основной поперечной моде резонатора легко определить из формулы (25) работы [2]:

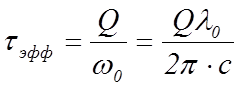                                                   ,                                                                 (33)

где  - центральная частота этой моды,  - ее длина волны, с- скорость света в вакууме. Из (33) следует

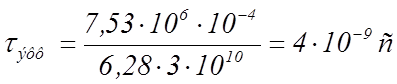                                       .                                                                 (34)

Ширина резонансной кривой, описывающей форму спектральной линии резонатора на частоте основной поперечной моды, может быть вычислена из формулы (37) работы [2]:

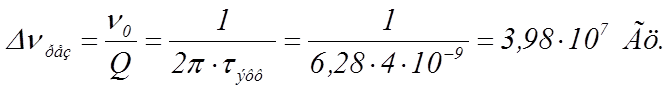                                                                            (35)

4.  Определение степени устойчивости резонатора

Известно, что в геометрическом приближении условие устойчивости резонатора имеет вид (см. формулу (53) в работе [2])

                                                       ,                                                                 (36)

где 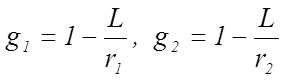 являются обобщенными параметрами резонатора. Вычисление этих параметров дает

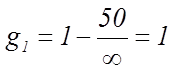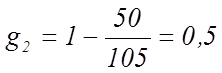                                     ,                                                                       (37)

Произведение  удовлетворяет условию (36), следовательно, резонатор является устойчивым.

5.  Определение частотного спектра лазерного излучения

Резонатор лазера существенным и даже принципиальным образом влияет на свойства выходного излучения. Дело в том, что при своем распространении внутри резонатора между его зеркалами излучение формируется в определенное состояние электромагнитного поля, которые называются типами колебаний резонатораили модами. Каждая мода характеризуется определенной пространственной структурой этого поля (т. е. определенным распределением амплитуды и фазы) в поперечном к оси резонатора направлении, в частности на поверхности зеркал резонатора. Кроме того, каждая мода характеризуется определенным сдвигом фазы за двойной проход резонатора.