Студенты инженерно-физического факультета, обучающиеся по специальности 120700 ²Машины и технология высокоэффективных процессов обработки², а также в бакалавратуре и магистратуре направления 553100 “Техническая физика”, значительный объем часов своих занятий посвящают изучению устройства и принципов действия различных лазеров, а также особенностей их применения на практике (в науке, технике и технологии, биологии и медицине и т.д.). Фактически это изучение начинается уже в четвёртом семестре и включает в себя освоение нескольких дисциплин:
4-ый семестр - ²Оптика и ядерная физика ²;
5-ой семестр - ²Спектроскопия атомов и молекул ²;
6-ой семестр - ²Физические основы генерации лазерного излучения²;
7-ой семестр - ²Лазерная техника²;
8-ой семестр - ²Применение лазеров²;
10-ый семестр - ²Нелинейная оптика²;
11-ый семестр - ²Оптическая спектроскопия².
Первая из перечисленных дисциплин знакомит студентов с общими представлениями, явлениями и законами оптики, а вторая - с различными спектральными характеристиками разнообразных атомарных и молекулярных сред, используемых в качестве активных элементов в лазерах. Общий фундамент для понимания физических основ генерации лазерного излучения закладывается в шестом семестре при изучении третьей дисциплины. После этого, в седьмом семестре, студенты изучают наиболее распространенные, а также наиболее перспективные лазерные системы, их важнейшие узлы и элементы. В дальнейшем им читаются спецкурсы, посвященные конкретным применениям лазеров.
Особенностью этого непрерывного погружения в мир лазерной техники является то, что, наряду с лекционными, практическими и лабораторными занятиями, студенты выполняют расчетно-графические задания (в четвёртом и пятом семестрах) и курсовые работы (в шестом, седьмом и восьмом семестрах). В настоящих методических указаниях приводятся варианты заданий курсовой работы шестого семестра, даются рекомендации и примеры их выполнения и порядок защиты. Курсовая работа по дисциплине ²Физические основы генерации лазерного излучения² выполняется в течении всего семестра по мере освоения материала. Она включает решение задач по трем основным разделам этой дисциплины, в том числе с применением вычислительной техники, построение графиков полученных зависимостей и их анализ. Поэтому каждый вариант курсовой работы разбит на три задания, соответствующих этим разделам.
Дана усиливающая среда, представляющая собой газ
двухуровневых атомов (рис.1), приведенный в состояние инверсной заселенности с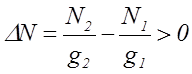 
. Концентрация атомов среды 
, длина среды l. Форма спектральной линии атомного перехода обусловлена
ударным уширением с шириной линии 
. Длина волны
перехода 
, его сила осциллятора 
. На вход среды поступает
слабый монохроматический сигнал с резонансной атомному переходу частотой и с
интенсивностью 
. Уровни
атомного перехода не являются вырожденными. Показатель нерезонансных потерь
среды равен b.
Требуется выполнить следующие расчеты:
1. Определить коэффициенты Эйнштейна для атомного перехода 2«1.
2. Определить величину интенсивности насыщения среды.
3. Определить величину показателя линейного усиления среды.
4. Составить
программу для вычисления, анализа и оптимизации на компьютере интенсивности
сигнала на выходе усилителя 
в
зависимости:
а) от длины среды, считая L переменной величиной;
б) от интенсивности входного сигнала, считая ее переменной величиной;
в) от показателя линейного усиления, считая его переменой величиной;
г) от показателя нерезонансных потерь, считая его переменой величиной.
5. Определить коэффициент усиления среды.
6. Сделать выводы в целом по выполненному заданию №1.
 |
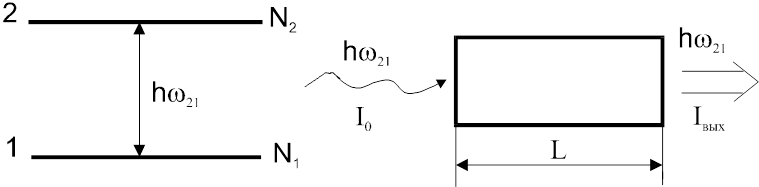Рис.1
Считать, что усилитель работает в стационарном режиме, а входной сигнал имеет форму плоской волны. Варианты задания указаны в табл.1. При выполнении расчетов по пункту 4 требуется решить только одну из четырех указанных задач (ее номер приведен в последней колонке задания №1 в табл.1).
Перед тем, как приступить к выполнению задания необходимо тщательно изучить материал работы [1], изложенный в ее разделах 1-5. Кроме того, необходимо освежить в памяти те сведения об атомных характеристиках, которые изучались в течении пятого семестра в рамках дисциплины «Спектроскопия атомов и молекул». Затем следует четко сформулировать условия задачи соответствующего варианта, перечислить искомые параметры и характеристики и сопроводить все это соответствующими рисунками и схемами. После того, как необходимые приготовления сделаны следует приступить к последовательному выполнению пунктов задания. Пример выполнения первого варианта данного задания приведен в приложении.
Данлазер, работающий в стационарном режиме. Его резонатор образован двумя плоскими зеркалами, одно из которых «глухое», а другое - полупрозрачное с коэффициентом отражения R. Характеристики активной среды лазера аналогичны характеристикам усиливающей среды, приведенным в табл.1 предыдущего задания.
Требуется выполнить следующие расчеты:
1. Определить коэффициент превышения генерации над порогом.
2. Определить пороговое значение длины активной среды и максимальную выходную интенсивность излучения лазера при бесконечной длине.
3. Определить оптимальную длину активной среды, необходимую для достижения максимального КПД лазера.
4. Определить интервал возможных значений коэффициента отражения выходного зеркала лазера.
5. Рассчитать выходную интенсивность лазерного излучения при оптимальных значениях коэффициента отражения выходного зеркала. Построить соответствующие графики и проанализировать их.
6. Сделать выводы в целом по заданию №2.
Расчеты следует выполнять в приближении плоских монохроматических волн. Варианты задания приведены в табл.1, где указаны только значения R. Значения остальных величин и параметров следует брать из соответствующего варианта табл.1 предыдущего задания.
Прежде чем приступить к выполнению задания следует тщательно изучить материал работы [1], изложенный в ее разделе 6. При расчетах считать, что выполняется условие (188) из [1]. Пример выполнения первого варианта данного задания приведен в приложении.
Резонатор лазера длиной L образован двумя сферическими зеркалами круглой формы. Радиусы кривизны отражающих поверхностей зеркал равны r1 и r2, коэффициенты их отражения - R1 и R2 соответственно, а диаметры одинаковы и равны 2а. Резонатор съюстирован с точностью до угла g.
Требуется выполнить следующие расчеты:
1. Определить число Френеля для данного резонатора.
2. Определить коэффициент полных потерь излучения в резонаторе на частоте основной поперечной моды. При этом считать, что основной вклад в них дают потери на пропускание зеркал, потери из-за неточности юстировки резонатора и дифракционные потери.
3. Определить добротность резонатора на частоте основной поперечной моды, время жизни фотона в этой моде и ширину резонансной кривой резонатора.
4. Определить, является ли данный резонатор устойчивым.
5. Определить частотный спектр мод резонатора, считая его пассивным.
6. Определить пространственные характеристики лазерного излучения.
7. Сделать выводы в целом по заданию №3.
Варианты заданий приведены в табл.1. Прежде чем приступить к выполнению задания следует тщательно изучить материал, изложенный в работах [2, 3]. Пример выполнения первого варианта данного задания и его оформления приведен в приложении.
Следует иметь в виду следующие два обстоятельства. Во-первых, некоторые студенты слишком формально подходят к выполнению этой работы. Они ограничиваются лишь тем, что, используя приведённый в приложении пример решения первого варианта заданий, подставляют вместо значений его параметров соответствующие значения из своего варианта. Во-вторых, полученные результаты ими зачастую не анализируются и, следовательно, не осознаётся физический смысл полученных графических зависимостей. Очевидно, что при таком подходе совершенно теряется смысл в выполнении данной работы, поскольку никаких практических навыков по расчёту лазерных систем в этом случае будущий инженер приобрести не сможет. А ведь именно в этом состоит назначение этой работы.
Чтобы избежать подобных ситуаций мы решили пойти следующим путём. Значения параметров всех вариантов, кроме первого, представленные в таблице 1, выбраны таким образом, что при их формальной подстановке в соответствующие формулы в некоторых случаях могут получиться абсурдные результаты. Тогда надо поступить следующим образом: изменить значения параметров задания таким образом, чтобы вновь полученный результат был физически оправдан. Но изменять надо не все параметры, а только их минимальное число.
Поясним сказанное на примере выполнения задания № 1, в
котором используется девять параметров. Допустим, выполняется пункт 4 этого
задания и строится зависимость 
.
Если полученная кривая выходит на насыщение, то это позволит провести её
оптимизацию. В противном случае оптимизация невозможна. Поэтому из девяти
параметров необходимо изменить значения одного из них, чтобы получить кривую
требуемого вида. Если этого недостаточно, то следует изменить значения двух
параметров и т. д. Но всегда следует иметь в виду, что число изменённых
параметров должно быть наименьшим.
Все свои действия необходимо подробно пояснять. Например, почему изменяете именно этот параметр, а не другой; почему вы его уменьшаете, а не увеличиваете (или наоборот); почему при построении графической зависимости выбран именно данный масштаб, а не другой и т. д. и т. п. Это учитывается при защите курсовой работы на кафедре и существенно влияет на результат.
Очевидно, что при подобном подходе от студента потребуется всестороннее знание физических закономерностей рассматриваемых процессов, которые и необходимо приобрести будущему инженеру-физику.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
