




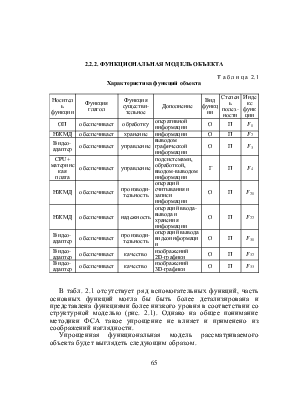

















2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ФСА
Методика и отдельные процедуры ФСА достаточно подробно описаны в литературе [1, 2, 7, 12]. Большая часть перечисленных выше процедур ФСА может быть непосредственно применена в рамках дипломных проектов к любому совершенствуемому или проектируемому объекту или системе. Менее подробно описаны процедуры, касающиеся формирования и выбора вариантов реализации отдельных функций объекта и, как следствие, – окончательного выбора варианта проекта. Дело в том, что количество вариантов реализации отдельных функций объекта может быть весьма большим, а количество вариантов их парного сравнения – вообще плохо обозримым. Кроме этого, процедура морфологического анализа является эвристической и не гарантирует выбора наилучшего сочетания стоимостных и качественных характеристик объекта. Поэтому в дополнение к традиционным процедурам ФСА естественно использовать подход к формированию и выбору наилучших сочетаний функциональных и стоимостных характеристик объекта посредством экономико-математической модели (ЭММ).
2.1. Использование оптимизационных
моделей в рамках ФСА
Рассмотрим один из вариантов ЭММ, не затрагивая различных аспектов построения, выбора и сравнительного анализа самих моделей, поскольку все это входит в задачи совсем других курсов. В соответствии с методикой ФСА в качестве критерия эффективности в модели можно использовать комплексный показатель качества. В самом простом варианте – это линейная свертка критериев степени достижения отдельных функциональных свойств объекта, взвешенных в соответствии со значимостью отдельных функций [1]. В соответствии с той же методикой другим важнейшим показателем является стоимостная оценка всего проекта.
Введем следующие обозначения:
L – множество уровней структуризации функций;
Jl – множества функций l-го уровня;
vlj – множества вариантов реализации j-й функции l-го уровня;
rlj – значимость j-й функции l-го уровня;
yljv – степень исполнения j-й функции l-го уровня при v-м варианте реализации;
yljэ – эталонное значение степени исполнения j-й функции l-го уровня;
yljп – пороговое значение степени исполнения j-й функции l-го уровня;
xljv – переменная выбора варианта реализации j-й функции l-го уровня:
![]() 1 – если выбирается v-й
вариант реализации j-й функции l-го
уровня;
1 – если выбирается v-й
вариант реализации j-й функции l-го
уровня;
xljv =
0 – в противном случае;
при этом 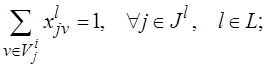
cljv – затраты на
осуществление j-й функции l-го уровня при
v-м варианте реализации;
Qоб – комплексный показатель качества;
P – сумма, необходимая для реализации проекта;
Pmax – максимальная сумма, выделяемая для реализации проекта.
Тогда ЭММ выбора наилучшего варианта реализации проекта (модернизации объекта при корректирующей форме ФСА) можно формально представить в следующем виде:
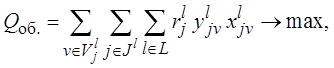 (2.1)
(2.1)
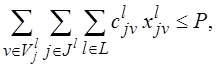 (2.2)
(2.2)
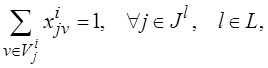 (2.3)
(2.3)
![]() (2.4)
(2.4)
Линейный функционал (2.1), выражающий обобщенный критерий качества, имеет ряд недостатков. Основным из них является возможность выбора вариантов исполнения отдельных функций с недопустимыми качественными характеристиками.
Альтернативным критерием может служить сумма квадратов отклонений выбираемых вариантов реализации отдельных функций от некоторых эталонных значений.
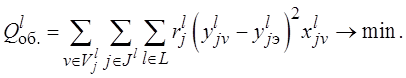 (2.5)
(2.5)
При использовании же критерия (2.1) следует добавить ограничения на пороговые (минимальные) значения уровней исполнения отдельных функций:
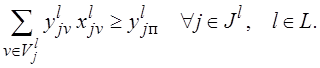 (2.6)
(2.6)
Вариантов реализации ЭММ на основе условий (2.1–2.6) может быть несколько. Кроме задаваемого непосредственно условиями (2.1)–(2.4), (2.6), можно рассмотреть вариант ЭММ с использованием в качестве критерия эффективности минимума затрат (2.2) на осуществление проекта при заданных качественных характеристиках [при ограничениях на показатели (2.1) и (2.6)]. Третий вариант – использование двух критериев эффективности (2.1) и (2.2). В этом случае определяются Парето-оптимальные варианты реализации проекта с последующим выбором окончательного варианта лицом, принимающим решения (ЛПР) в соответствии со своей системой предпочтений. Разновидностью этого же подхода является параметрический анализ модели (2.1)–(2.4), (2.6), где в качестве параметра рассматривается P – цена проекта, при соблюдении дополнительного ограничения:
![]() (2.7)
(2.7)
В результате параметрического анализа ЭММ генерируется множество вариантов решений, при этом окончательный выбор единственного из них также остается за ЛПР. Еще одной разновидностью использования одновременно двух критериальных показателей является их свертка. В ФСА, в частности, используется отношение «значимость/затраты» («качество/затраты») или «затраты/значимость» [1]. Такая свертка будет выглядеть следующим образом:
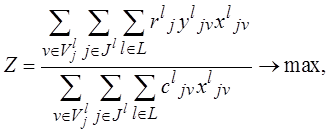 или
или ![]()
В реальных условиях ЭММ могут дополняться ограничениями на количественные (ресурсные) характеристики объекта (проекта), что существенно расширяет возможности методик ФСА, как средств анализа и разработки управленческих решений. В связи с этим следует отметить явную связь ФСА через посредство ЭММ с методами оптимального проектирования.
Рассмотрим численный пример применения методики ФСА с использованием изложенного подхода.
2.2. Пример применения оптимизационной
модели в методике ФСА
Пусть перед ЛПР стоит задача выбора наилучшей комплектации компьютера для нужд производственного процесса. Для простоты ограничимся выбором комплектующих системного блока, поскольку задача комплектования вычислительного комплекса в целом, включая программное обеспечение, внешние устройства и средства связи, ничем не отличается от данной задачи, за исключением объема исходных данных и размерности формируемой ЭММ. Данный объект выбран не случайно. Дело в том, что из-за наличия на рынке огромного числа комплектующих любой мало-мальски квалифицированный пользователь, полномочный принимать соответствующие решения, при желании может выступить в роли конструктора, не полагаясь на типовые, как правило, самые дешевые комплектации, а скомпоновав себе компьютер в соответствии со своими финансовыми возможностями и предпочтениями. В точности так же ведет себя профессиональный конструктор при проектировании любого другого технического объекта, используя типовые решения, узлы или блоки; администратор, формируя организационную структуру своего подразделения. В любом случае перед ЛПР стоит проблема выбора таких состава и структуры объекта, которые бы обеспечивали, с точки зрения ЛПР, наивысшую эффективность функционирования объекта.
В соответствии с общей схемой ФСА построим структурную и функциональную модели объекта.
2.2.1. Структурная модель объекта
Укрупненно, структурную модель системного блока IBM – совместимого персонального компьютера со стандартной архитектурой – можно представить следующим образом (рис. 2.1).
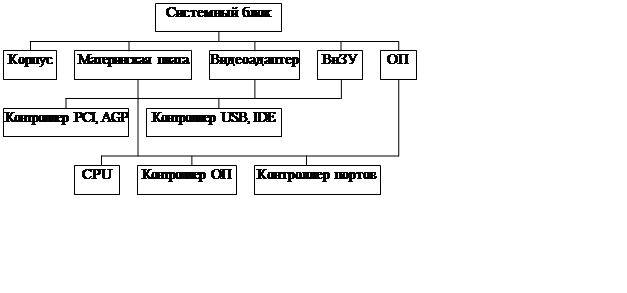 |
Рис.2.1. Структурная модель системного блока персонального компьютера
Используемые сокращения и обозначения:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.