Математические модели в функционально-стоимостном анализе, страница 4

q₃₁₁= 0,01*(1*0,5*30+3*0,3*5+3*0,2*4) = 0,219 …  и т.д.

В соответствии с (2.13), вычислим все коэффициенты q_jvi и занесем их в табл. 2.7–2.10.

Т а б л и ц а  2.7

Матрица коэффициентов комплексного показателя качества для F₁

j = 1,   (ОП)	v=  i=	1	2	3
		(SDRAM.133)	(RDRAM)	(DDR SDRAM)
(128 Мб)	1	2,445	2,56725	2,5917
(256 Мб)	2	4,89	5,1345	5,1834

Минимальное значение показателя качества ОП будет равно 2,445 при 128 Мб и цене $33. Максимальное значение – 15,5502(5,1834*3) при 768 Мб и цене $258.

Т а б л и ц а  2.8

Матрица коэффициентов комплексного показателя качества для F₂

j = 2,  (НЖМД)	v= i=	1	2	3	4	5
		Fujitsu	IBM	Maxtor	Quantum	Seagate
(10 Гб)	1	4,965	5,31255	4,18053	3,91242	4,31955
(20 Гб)	2	9,93	10,6251	8,36106	7,82484	8,6391
(40 Гб)	3	19,86	21,2502	16,72212	15,64968	17,2782

Минимальное значение показателя качества НЖМД будет равно 3,91242 при емкости 10 Гб и цене $70. Максимальное значение – 42,5004(21,2504*2) при емкости 2*40 = 80 Гб и цене $230.

Т а б л и ц а  2.9

Матрица коэффициентов комплексного показателя качества для F₃

j = 3, (Видеоадаптер)	v=   i=	1	2	3	4
		Nvidia	S3	Matrox	ATI Tecnology
	1	0,219	0,112	0,148	0,27

Минимальное значение показателя качества видеоадаптера будет равно 0,112 при цене $30. Максимальное значение – 0,27 при цене $100.

Т а б л и ц а  2.10

Матрица коэффициентов комплексного показателя качества для F₄

j = 4, (Процессор)	v= i=	1	2	3	4
		Pentium III	Celeron	Duron	Athlon
(тактовая частота 850 Мгц)	1	14,384	9,92	12,4	17,856
(тактовая частота 1,2 Ггц)	2	19,344	12,896	17,36	22,32

Минимальное значение показателя качества процессора будет равно 9,92 при цене $180. Максимальное значение – 22,32 при цене $220.

Простой расчет показывает, что значения Q_об лежат в интервале:

Q_minQ_обQ_max,

где Q_min = 16,38942 [баллов], Q_max = 80,6406 [баллов].

Наихудшему качеству соответствует цена $313, наилучшему – $808.

При этом ценовой диапазон (2.7) составит P_minPP_max:

P_min = 33 + 65 + 30 + 150 = $278;

P_max = 88*3 + 115*2 + 100 + 260 = $854.

Заметим, что наихудшее качество не соответствует наименьшей цене, а наилучшее – наибольшей.

С учетом вновь введенных обозначений, опираясь на (2.1), запишем

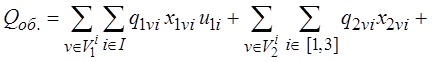
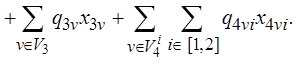                        (2.14)

Обозначим первое слагаемое в формуле (2.14) через Q₁, вто-
рое – через Q₂, третье – через Q₃, четвертое – через Q₄, т.е.

Q_об = Q₁ + Q₂ + Q₃ + Q₄.

2.3.3. Стоимостная оценка комплектации

Пусть c_jvi – цена комплектующего при реализации функции j при v, i-варианте комплектации. Тогда, опираясь на (2.2), запишем выражение для стоимостной оценки комплектации системного блока:

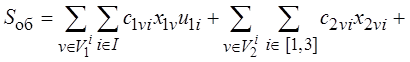
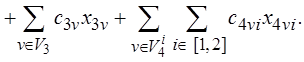                       (2.15)

Также обозначим первое слагаемое в формуле (2.15) через S₁, второе – через S₂, третье – через S₃, четвертое – через S₄, т.е.

S_об = S₁ + S₂ + S₃ + S₄.

2.3.4. ресурсные ограничения

Используя полученные выше оценки, запишем ограничения задачи:

P_minS_обP_max,                                  (2.16)

Q_minQ_обQ_max.                                 (2.17)

Кроме этого, естественным  является ограничение по финан-сам (2.2):

S_обP.                                         (2.18)

Ограничения на ряд технических характеристик. В частности, можно потребовать обеспечения минимально необходимой емкости ОП (E₁) и НЖМД (E₂):

                             (2.19)

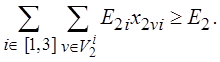                            (2.20)

Такой же характер носит ограничение (2.12).

2.3.5. Логические ограничения

К числу логических ограничений можно отнести все условия (2.8)–(2.11). Их список следует дополнить:

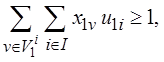                                  (2.21)

либо вместо (2.19) и (2.21) использовать одно:

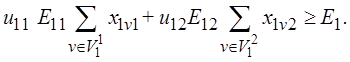               (2.22)

2.3.6. Критерии эффективности

В качестве критерия, как уже упоминалось, целесообразно использовать обобщенный показатель качества (2.14), тогда
Q_обmax; либо критерий минимума затрат на комплектацию (2.15), тогда S_обmin. И в том и в другом случае возможен параметрический анализ соответственно показателей цены и качества. И, наконец, дополнительное решение и оценку эффективности позволяет получить использование критерия «качество/затраты»:

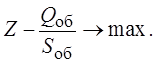                                 (2.23)

В совокупности получаем формальную запись ЭММ: ограничения (2.8)–(2.12), (2.16)–(2.18), (2.20), (2.22) и критерии (2.14), (2.15), (2.23). Для краткости назовем ее задачей (2.8)–(2.23).

2.3.7. Варианты реализации ЭММ

Несколько замечаний относительно сформулированной ЭММ. Несмотря на кажущуюся простоту задачи и дополнительное предельное упрощение, построенная модель позволяет получить представление о сложности задач формирования и выбора решений. Некоторое представление можно составить и о формальном аппарате решения подобных проблем.