Математические модели в функционально-стоимостном анализе, страница 5

Основной особенностью модели является дискретность переменных (большинство из них – булевы) и логические ограничения, позволяющие реализовать высказывания заданной сложности. Еще одной «неприятностью» является наличие нелинейных (квадратичных), относительно неизвестных, компонентов в выражениях (2.14), (2.15), (2.21)–(2.23). Известно, что подобные задачи являются NP-трудными и при больших размерностях требуют значительных затрат времени и вычислительных ресурсов. Однако, если не выходить за рамки методик ФСА, формируемые модели имеют блочные структуры и всего по одному связующему ограничению (2.18). Подобные задачи легко подвергаются декомпозиции (разбиению на более мелкие подзадачи по числу блоков) и, как правило, достаточно просто решаются точными методами.

Еще один прием, используемый для упрощения исходных условий и носящий в литературе название «метод генерации столбцов» [5], можно применить и к нашей задаче в целях исключения нелинейных зависимостей. Суть его состоит в следующем.

Все нелинейные компоненты в задаче связаны с формализацией логических и количественных условий выбора микросхем памяти (функция F₁). Если вместо переменных выбора x_1v , и количественных u_1i, i = 1,2 ввести новые неизвестные переменные выбора из всех возможных вариантов комплектации ОП, то мы тем самым освобождаемся от необходимости использования произведений переменных во всех выражениях. Однако такое упрощение приводит к значительному росту числа неизвестных в задаче. Для иллюстрации перечислим формируемое при этом множество вариантов комплектации (каждому варианту соответствует отдельная переменная). Если v – индекс типа микросхем
(v = 1,3) (см. табл. 2.7), e – индекс емкости микросхемы памяти
(e = 1,2, если e = 1, то 128 К, если e = 2, то 256 К), i – количество микросхем (i = 1,3), то множество вариантов можно перечислить тройками или комбинациями троек: {111, 211, 311, 121, 221, 321, 111+121, 211+221, 311+321, …}. Общее количество допустимых комбинаций составит 3*6 = 18. Первый сомножитель (3) – количество типов микросхем, второй (6) – число возможных значений емкости ОП (128, 256, …, 768). Таким образом, вместо 5 неизвестных получаем минимум 18 (максимум N₁ = 27), что приводит к росту общего количества неизвестных более чем в 1,5 раза. Однако при этом нелинейные составляющие Q₁, S₁ и другие в выражениях (2.14), (2.15), (2.21) – (2.23) становятся линейными. Разумна ли такая плата за упрощение – необходимо решать по обстоятельствам в каждом конкретном случае.  Дело  в  том, что количество генерируемых вариантов (новых переменных) может достигать чрезмерных значений[5].

2.4. Оптимизационные расчеты и анализ

вариантов решения средствами MS EXCEL

Сформированная выше модель легко реализуется средствами MS EXCEL. Соответствующие EXCEL-таблицы (файл с именем ФСА.xls) представлены на рис. 2.3 – 2.6.

На рис. 2.4, а, б приведены фрагменты EXCEL-таблицы с исходными данными, промежуточными вычислениями и результатами оптимизационных расчетов. Первый фрагмент содержит исходные данные из табл. 2.2 – 2.5, коэффициенты значимости функций первого уровня – табл. 2.6 и промежуточные вычисления – в соответствии с табл. 2.7 – 2.10 по формулам (2.13).

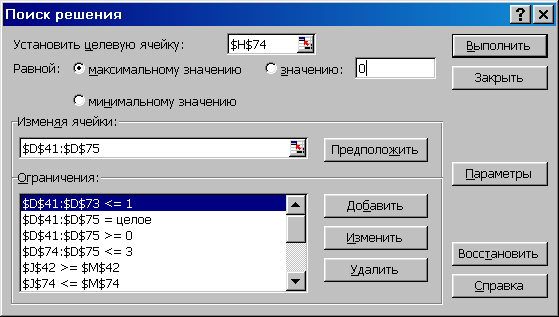
Рис. 2.3, а. Окно надстройки «Поиск решения».

Первый фрагмент условий задачи

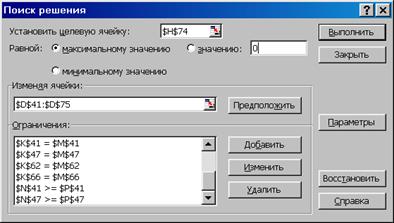
Рис. 2.3, б. Окно надстройки «Поиск решения».

Второй фрагмент условий задачи

Второй фрагмент (рис. 2.4, б) отображает данные модели (2.8) – (2.23): переменные – ячейки D41 – D43, D47 – D75, имена переменных (C41 – C43, C47 – C75), коэффициенты q_jvi (E41 – E73) и c_jvi (F41 – F73), соответствие которых условиям (2.8) – (2.23) дополнительных пояснений не требует.

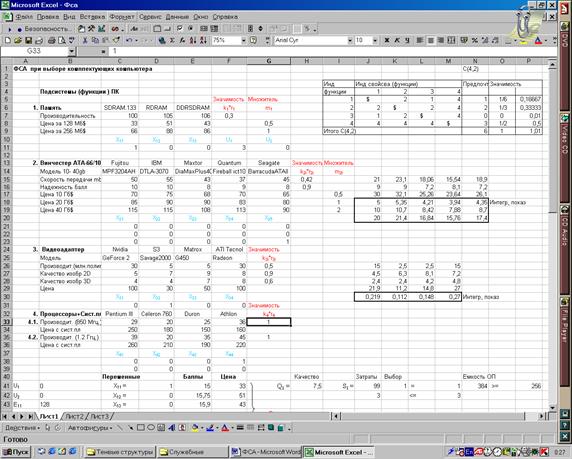
Рис. 2.4, а. Первый фрагмент EXCEL-таблицы с задачей (2.8) – (2.23)

Ячейки H41, H47, H62, H66 содержат значения соответственно Q₁, Q₂, Q₃, Q₄; H74 – выражение (2.14), т.е. Q_об. Ячейки J41, J47, J62, J66 содержат значения соответственно S₁, S₂, S₃, S₄; J74 – выражение (2.15), т.е. S_об. Ячейки K41, K47, K62, K66 содержат левые части условий выбора (2.8), (2.9), (2.10), (2.11) соответственно. Ячейка J42 соответствует левой части ограничения (2.12). Ячейка N41 содержит левую часть ограничения (2.19). Ячейка N47 содержит левую часть ограничения (2.20).

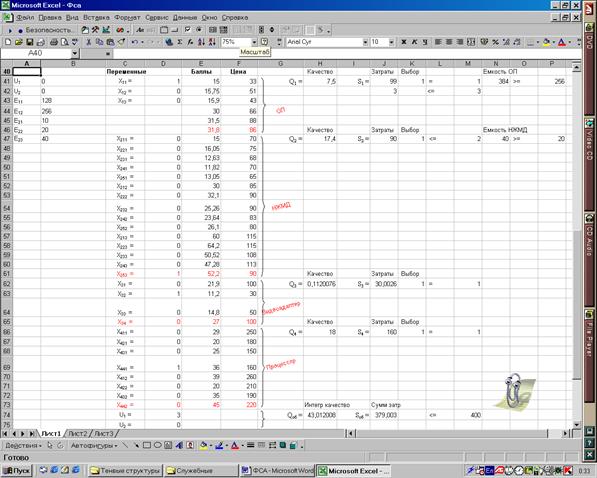
Рис. 2.4, б. Второй фрагмент EXCEL-таблицы с задачей (2.8) – (2.23)

Ячейки M41, M42, M47, M62, M66, P41, P47 содержат правые части ограничений (2.8), (2.9), (2.10), (2.11), (2.12), (2.19) и (2.20) соответственно. Ячейка M74 соответствует значению P – правой части ограничения (2.18). На рис. 2.4, б это значение равно $400.

Для решения оптимизационных задач в EXCEL используется надстройка «Поиск решения». Данное средство вызывается из меню Сервис (рис. 2.6). На рис. 2.3, а и 2.3, б отображено диалоговое окно процедуры поиска решения, в котором задаются: целевая ячейка (соответствует критерию эффективности), переменные задачи (окно «изменяя ячейки») и ограничения задачи (окно «ограничения»). Все данные вводятся из EXCEL-таблицы
(рис. 2.4, а и 2.4, б) с помощью стандартных диалогов Windows. В диалогах создаются ссылки на ячейки, содержащие формулы – ограничения задачи и критерий эффективности. Рис. 2.3, а и б отображают все необходимые условия для решения задачи (2.8) – (2.23).

Кроме этого, для успешного поиска оптимальных решений задачи (2.8) – (2.23) необходимо установить дополнительные параметры вычислений (кнопка «параметры»). Их значения приведены на рис. 2.5.

На рис. 2.4, б приведен также один из результатов оптимизационных расчетов, отображаемый в ячейках переменных и ограничений. Этот результат интерпретируется следующим образом:

1) x₁₁ = 1, u₁₁ = 3, u₁₂ = 0, что означает выбор типа ОП SDRAM.133, 3 микросхем по 128Мб. Общая емкость ОП составит при этом 384 Мб, цена – $99, Q₁ = 7,5 балла;