Анализ микроданных обследования о расходах на определенную группу услуг (налоги) и уровня благосостояния домохозяйств по выбранному территориальному округу, страница 8

a  Dependent Variable: LnY

Оценки значимых параметров изменились незначительно, значит, этот признак мультиколлиниарности отсутствует.

- Все оценки параметров имеют логичные знаки и величины с экономической точки зрения, значит, этот признак отсутствует.

- У всех значимых оценок  коэффициентов регрессии имеются небольшие стандартные ошибки и большая значимость, в то время, как всё уравнение в целом значимо (большое значение коэффициента детерминации). Значит, этот признак мультиколлинеарности отсутствует.

Так как все три признака не выполняются, значит, мультиколлинеарность отсутствует.

3)  Регрессионная модель 3.

Таблица 39 – Дисперсионный анализ

Model		Sum of Squares	df	Mean Square	F	Sig.
1	Regression	4141,251	2	2070,626	8228,478	,000(a)
	Residual	9632,784	38280	,252
	Total	13774,035	38282

a  Predictors: (Constant), F2, F1

b  Dependent Variable: LnY

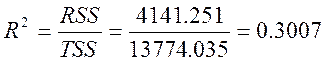
Таблица 40 – Сводка для модели

Model	R	R Square	Adjusted R Square	Std. Error of the Estimate
1	,548(a)	,301	,301	,50164

a  Predictors: (Constant), F2, F1

Значения коэффициента детерминации рассчитанного вручную и взятого из таблицы совпали. Значение коэффициета далеко от 1, значит, уравнение не совсем точно описывает данные.

И так как F_ст.>F_кр., модель в целом является значимой. Значит, эту модель можно использовать для прогнозирования.

Сделана проверка на мультиколлинеарность.

- Изменены исходные данные путем изъятия малого количества (3) наблюдений и оценены неизвестные параметры (табл.41).

Таблица 41 - Коэффициенты

Model		Unstandardized Coefficients		Standardized Coefficients	t	Sig.
		B	Std. Error	Beta
1	(Constant)	7,320	,022		338,458	,000
	F1	1,41E-005	,000	8,945	40,348	,000
	F2	-1,08E-006	,000	-8,362	-37,717	,000

a  Dependent Variable: LnY

Оценки значимых параметров изменились незначительно, значит, этот признак мультиколлиниарности отсутствует.

- Все оценки параметров имеют логичные знаки и величины с экономической точки зрения, значит, этот признак отсутствует.

- У всех значимых оценок  коэффициентов регрессии имеются небольшие стандартные ошибки и большая значимость, в то время, как всё уравнение в целом значимо (большое значение коэффициента детерминации). Значит, этот признак мультиколлинеарности отсутствует.

Так как все три признака не выполняются, значит, мультиколлинеарность отсутствует.

9.  На рисунке 18 изображены исходные данные и все три линии регрессии.

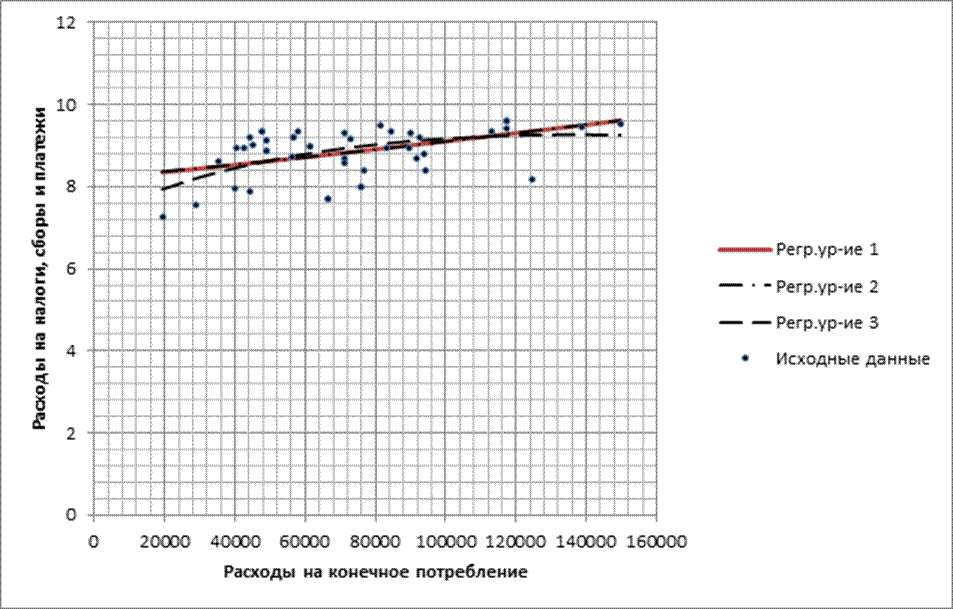
Рисунок 18 – Исходные данные и линии регрессии

10.  Выбрано наилучшее регрессионное уравнение: регрессионная модель 3, уравнение которой выглядит следующим образом:

У данной модели коэффициент детерминации выше, чем у двух других и по графику видно, что линия, построенная по данному уравнению, ближе всего к исходным данным.

11.  Для выбранного уравнения построен 95%-ый доверительный интервал на всем диапазоне исходных данных.

Доверительный интервал и линия регрессии изображены на рисунке 19.

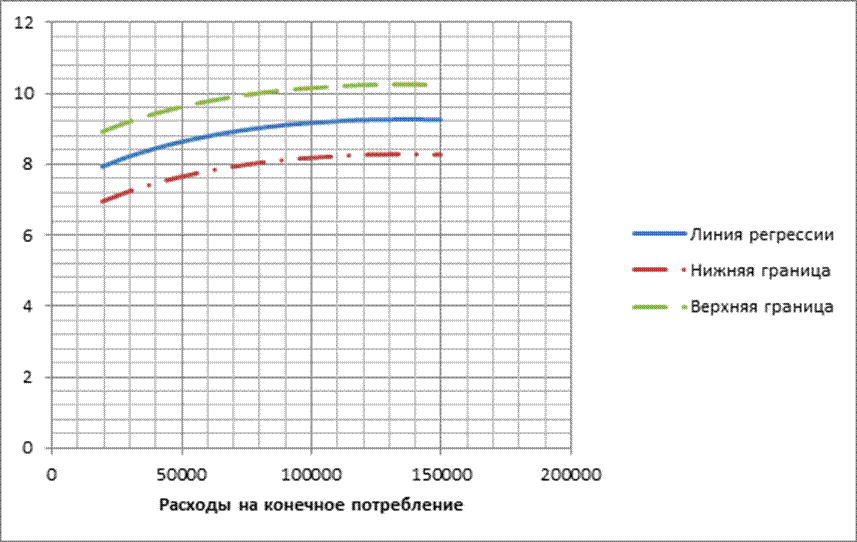
Рисунок 19 – Линия регрессии и доверительный интервал

12.  В ходе выполнения данной расчетно-графической работы была построена модель зависимости расходов населения определенной территории на уплату налогов, сборов и платежей от расходов на конечное потребление, наилучшим образом описывающая выявленные закономерности в пределах указанной территории и выбранного сегмента домохозяйств.

Для этого из исходных данных были исключены аномальные наблюдения и проведено нормализующее преобразование, в результате которого зависимая переменная приняла вид ln(у). Для дальнейшего анализа был выбран наиболее однородный сегмент домохозяйств.

Далее были рассчитаны коэффициенты корреляции: парные и частные.  Проверены на значимость и выбраны для дельнейшего анализа в качестве независимой переменной расходы на конечное потребление.

Затем были построены три регрессионные модели, проведен регрессионный анализ, и из исходных моделей впоследствии была выбрана одна, наилучшим образом описывающая исходные данные:

.

У данной модели коэффициент детерминации наибольший из трех моделей, значит она наилучшим образом описывает данные.

Список использованных источников

1.  Тимофеев В.С. Эконометрика: учебник / В.С. Тимофеев, А.В. Фаддеенков, В.Ю. Щеколдин. – Новосибирск : Изд-во НГТУ, 2011. – 346 с. (Серия «Учебники НГТУ»)

2.  Практикум по эконометрике: методическое пособие. – Новосибирск : Изд-во НГТУ.