Анализ микроданных обследования о расходах на определенную группу услуг (налоги) и уровня благосостояния домохозяйств по выбранному территориальному округу, страница 3

Произведена проверка на нормальность (гипотеза H₀: y ϵ N) распределения переменной DOLYA тремя способами:

1)  Ассиметрия, ексцесс.

Значения ассиметрии и эксцесса представлены в таблице 9.

Таблица 9 – Описательные статистики

	N	Skewness		Kurtosis
	Statistic	Statistic	Std. Error	Statistic	Std. Error
Dolya	331393	1,925	,004	9,444	,009
Valid N (listwise)	331393

Проверяем условия: |А|≤3*S_A; |Э|≤5*S_Э

1,925≥3*0,004; 9,444≥5*0,009

Оба условия не выполняются, поэтому гипотеза о нормальности распределения отвергается.

2)  С помощью критерия Колмагорова-Смирнова (табл. 10).

Условие: p < 0,05 – не нормальное распределение (p – Ассимпт.знч. (двустороннее))

Таблица 10 – Обновыборочный критерий Колмагорова-Смирнова

		Dolya
N		433
Normal Parameters(a,b)	Mean	,0915
	Std. Deviation	,07121
Most Extreme Differences	Absolute	,099
	Positive	,087
	Negative	-,099
Kolmogorov-Smirnov Z		2,070
Asymp. Sig. (2-tailed)		,000

a  Test distribution is Normal.

b  Calculated from data.

p=0,000, что меньше 0,05, значит гипотеза о нормальности распределения отвергается.

3) Графики для проверки нормальности (табл. 11).

Таблица 11 – Критерий нормальности

	Kolmogorov-Smirnov(a)
	Statistic	df	Sig.
Dolya	,114	331393	,000

a  Lilliefors Significance Correction

По критерию Колмагорова-Смирнова значимость равна 0,000, что меньше значения 0,05, поэтому распределение не является нормальным. Также это отражено на графиках (рис. 11,12).

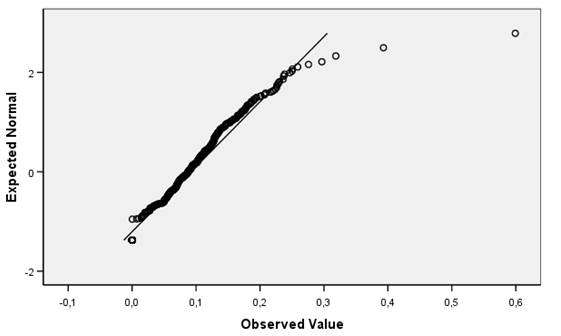
Рисунок 11 – Вероятностный график (квантили)

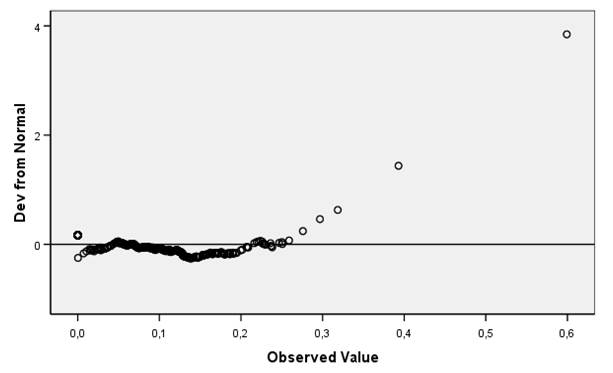
Рисунок 12 – Вероятностный график (квантили) с удаленным трендом

Проведено нормализующее преобразование.

Преобразование переменной: деление на количество взрослых членов домохозяйства.

Создана переменная DelVzrChl = nalog / (chlicn - chdet) (налоги / (число наличных лиц домохозяйств – фактическое число детей до 16 лет)).

Произведена проверка на нормальность (гипотеза H₀: y ϵ N) распределения переменной DelVzrChl тремя способами:

3)  Ассиметрия, ексцесс.

Значения ассиметрии и эксцесса представлены в таблице 12.

Таблица 12 – Описательные статистики

	N	Skewness		Kurtosis
	Statistic	Statistic	Std. Error	Statistic	Std. Error
DelVzrChl	331393	1,168	,004	2,448	,009
Valid N (listwise)	331393

Проверяем условия: |А|≤3*S_A; |Э|≤5*S_Э

1,168≥3*0,004; 2,448≥5*0,009

Оба условия не выполняются, поэтому гипотеза о нормальности распределения отвергается.

4)  С помощью критерия Колмагорова-Смирнова (табл. 13).

Условие: p < 0,05 – не нормальное распределение (p – Ассимпт.знч. (двустороннее))

Таблица 13 – Обновыборочный критерий Колмагорова-Смирнова

		DelVzrChl
N		433
Normal Parameters(a,b)	Mean	2427,2405
	Std. Deviation	1983,11706
Most Extreme Differences	Absolute	,110
	Positive	,076
	Negative	-,110
Kolmogorov-Smirnov Z		2,299
Asymp. Sig. (2-tailed)		,000

a  Test distribution is Normal.

b  Calculated from data.

p=0,000, что меньше 0,05, значит гипотеза о нормальности распределения отвергается.

3) Графики для проверки нормальности (табл. 14).

Таблица 14 – Критерий нормальности

	Kolmogorov-Smirnov(a)
	Statistic	df	Sig.
DelVzrChl	,115	331393	,000

a  Lilliefors Significance Correction

По критерию Колмагорова-Смирнова значимость равна 0,000, что меньше значения 0,05, поэтому распределение не является нормальным. Также это отражено на графиках (рис. 13,14).

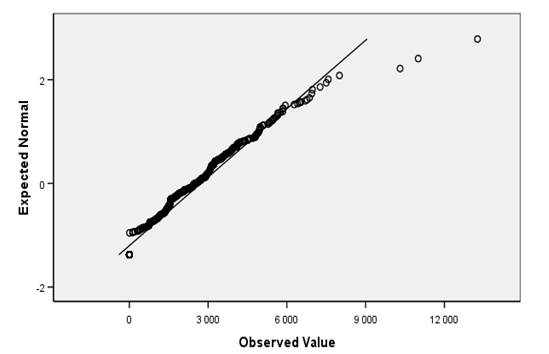
Рисунок 13 – Вероятностный график (квантили)

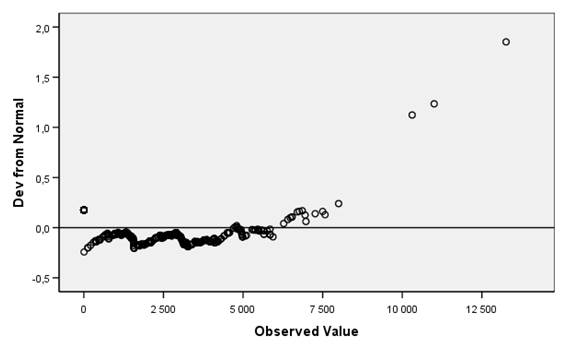
Рисунок 14 – Вероятностный график (квантили) с удаленным трендом

Проведено нормализующее преобразование.

Преобразование переменной: ln(y).

Создана переменная LnY = LN(nalog).

Произведена проверка на нормальность (гипотеза H₀: y ϵ N) распределения переменной LnYтремя способами:

5)  Ассиметрия, ексцесс.

Значения ассиметрии и эксцесса представлены в таблице 15.

Таблица 15 – Описательные статистики

	N	Skewness		Kurtosis
	Statistic	Statistic	Std. Error	Statistic	Std. Error
LnY	275467	-1,565	,005	7,194	,009
Valid N (listwise)	275467

Проверяем условия: |А|≤3*S_A; |Э|≤5*S_Э

1,565≥3*0,005; 7,194≥5*0,009

Оба условия не выполняются, поэтому гипотеза о нормальности распределения отвергается.

6)  С помощью критерия Колмагорова-Смирнова (табл. 16).

Условие: p < 0,05 – не нормальное распределение (p – Ассимпт.знч. (двустороннее))

Таблица 16 – Обновыборочный критерий Колмагорова-Смирнова

		LnY
N		353
Normal Parameters(a,b)	Mean	8,4537
	Std. Deviation	,78728
Most Extreme Differences	Absolute	,067
	Positive	,067
	Negative	-,066
Kolmogorov-Smirnov Z		1,258
Asymp. Sig. (2-tailed)		,084

a  Test distribution is Normal.