Анализ микроданных обследования о расходах на определенную группу услуг (налоги) и уровня благосостояния домохозяйств по выбранному территориальному округу, страница 4

b  Calculated from data.

p=0,084, что больше 0,05, значит гипотеза о нормальности распределения принимается.

3) Графики для проверки нормальности (табл. 17).

Таблица 17 – Критерий нормальности

	Kolmogorov-Smirnov(a)
	Statistic	df	Sig.
LnY	,086	275467	,000

a  Lilliefors Significance Correction

По критерию Колмагорова-Смирнова значимость равна 0,000, что меньше значения 0,05, поэтому распределение не является нормальным. Также это отражено на графиках (рис. 15,16).

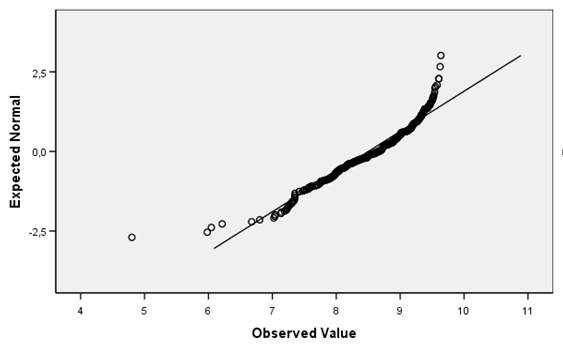
Рисунок 15 – Вероятностный график (квантили)

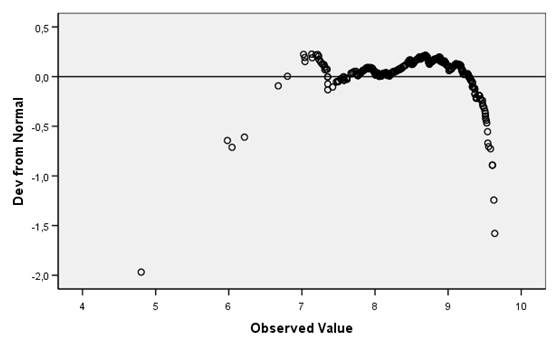
Рисунок 16 – Вероятностный график (квантили) с удаленным трендом

Так как по критерию Колмагорова-Смирнова третий вариант преобразований оказался нормальным, для дальнейшего исследования будет использоваться переменная LnY.

3.  Определена теснота взаимосвязи между налогами, сборами и платежами и качественными характеристиками домохозяйств. Для этого проверены гипотезы о независимости признаков на 5%-м уровне значимости. Способы проверки гипотез выбраны в зависимости от шкалы измерения характеристик.

Для количественных характеристик:

Число наличных членов домохозяйств.

В таблице 18 представлен ранговый коэффициент корреляции Спирмена.

Таблица 18 - Корреляции

			LnY	Число наличных лиц в домохозяйстве
Spearman's rho	LnY	Correlation Coefficient	1,000	,300(**)
		Sig. (2-tailed)	.	,000
		N	353	353
	Число наличных лиц в домохозяйстве	Correlation Coefficient	,300(**)	1,000
		Sig. (2-tailed)	,000	.
		N	353	433

**  Correlation is significant at the 0.01 level (2-tailed).

Фактическое число детей до 16 лет (табл.19).

Таблица 19 - Кореляции

			LnY	Фактическое число детей до 16 лет
Spearman's rho	LnY	Correlation Coefficient	1,000	,051
		Sig. (2-tailed)	.	,336
		N	353	353
	Фактическое число детей до 16 лет	Correlation Coefficient	,051	1,000
		Sig. (2-tailed)	,336	.
		N	353	433

Для номинальных шкал:

Тип населенного пункта.

Переменная y (ln(y)) переведена в номинальную шкалу.

Результаты представлены в таблице 20.

Таблица 20 – Таблица сопряженности

		LnY (Banded)											Total
		1	2	3	4	5	6	7	8	9	10	11
Тип насел пункта	Городская местность	11635	13616	16110	18146	14772	11648	15846	18922	10669	19487	23043	173894
	Сельская местность	11961	13270	10517	6975	8621	10631	11814	6036	13212	6738	1798	101573
Total		23596	26886	26627	25121	23393	22279	27660	24958	23881	26225	24841	275467

Результаты проверки хи-квадрат показывают степень соответствия наблюдаемых частот ожидаемым и представлены в таблице 21.

Таблица 21 – Хи-квадрат

	Value	df	Asymp. Sig. (2-sided)
Pearson Chi-Square	22239,986(a)	10	,000
Likelihood Ratio	24657,007	10	,000
Linear-by-Linear Association	7028,796	1	,000
N of Valid Cases	275467

a  0 cells (,0%) have expected count less than 5. The minimum expected count is 8214,94.

Значение хи-квадрат больше, чем  критическое значение при вероятности ошибки 0,05 (хи-квадрат(0.95,2)) равное 18,31. В этом случае можно говорить о зависимости между типом населенного пункта и величиной налогов, сборов и платежей.

Произведено разбиение совокупности всех домохозяйств на группы с разным набором характеристик (сегменты) – таблица 22. Выбраны следующие качественные признаки:

- тип населенного пункта;

- число наличных лиц в домохозяйстве (так как корреляция выше).

Таблица 22 – Разбиение на сегменты

Сегмент (код)	mest	chlicn
1	1	1
2	1	2
3	1	3
4	1	4
5	1	5-6
6	2	1
7	2	2
8	2	3
9	2	4
10	2	5-6

Рассчитаем коэффициенты вариации для данных сегментов (табл. 23).

Таблица 23 – Расчет коэффициента вариации

Сегмент (код)	mest	chlicn	y средн	Sу	Коэф. вариации
1	1	1	8,2817	0,00389	0,0004697
2	1	2	8,5373	0,00425	0,0004978
3	1	3	8,7444	0,00374	0,0004277
4	1	4	8,8748	0,00307	0,0003459
5	1	5-6	8,2760	0,00745	0,0009002
6	2	1	7,6976	0,00342	0,0004443
7	2	2	8,4558	0,00343	0,0004056
8	2	3	8,4938	0,00464	0,0005463
9	2	4	8,5463	0,00490	0,0005733
10	2	5-6	8,6173	0,00761	0,0008831