Анализ микроданных обследования о расходах на определенную группу услуг (налоги) и уровня благосостояния домохозяйств по выбранному территориальному округу, страница 7

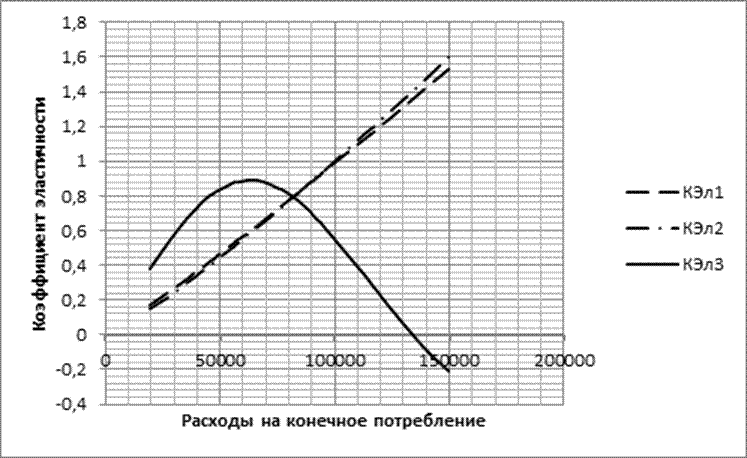
Рисунок 17 – Графики коэффициентов эластичности для уравнений регрессии

Частный коэффициент эластичности показывает, на сколько процентов изменится значение Y (зависимая переменная) при изменении X_i (независимая переменная) на 1% от заданного значения.

По графику на рисунке 17 можно сделать вывод, что в первой и второй регрессионной модели при увеличении у населения расходов на конечное потребление, будут расти уплачиваемые ими налоги, сборы и платежи. А коэффициенты эластичности для третьей модели показывают, что пока расходы на конечное потребление меньше примерно 65000, с их ростом будут расти расходы на налоги, сборы и платежи. Как только расходы на конечное потребление будут больше 65000, с их ростом расходы на налоги, сборы и платежи будут уменьшаться.

8.  Для каждого уравнения вычислен коэффициент детерминации. Каждое регрессионное уравнение проверено на значимость. Таблицы дисперсионного анализа представлены в таблицах 33, 36, 39. Значения коэффициентов детерминации посчитаны вручную и сопоставлены со значениями из таблиц 34, 37, 40. Сделаны заключения о возможном присутствии мультиколлинеарности в построенных уравнениях.

1)  Регрессионная модель 1.

Таблица 33 – Дисперсионный анализ

Model		Sum of Squares	df	Mean Square	F	Sig.
1	Regression	3535,094	1	3535,094	13216,822	,000(a)
	Residual	10238,941	38281	,267
	Total	13774,035	38282

a  Predictors: (Constant), F1

b  Dependent Variable: LnY

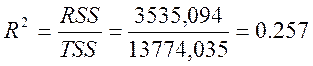
Таблица 34 – Сводка для модели

Model	R	R Square	Adjusted R Square	Std. Error of the Estimate
1	,507(a)	,257	,257	,51717

a  Predictors: (Constant), F1

Значения коэффициента детерминации рассчитанного вручную и взятого из таблицы совпали. Значение коэффициета далеко от 1, значит, уравнение не совсем точно описывает данные.

И так как F_ст.>F_кр., модель в целом является значимой. Значит, эту модель можно использовать для прогнозирования.

Сделана проверка на мультиколлинеарность.

- Изменены исходные данные путем изъятия малого количества (3) наблюдений и оценены неизвестные параметры (табл.35).

Таблица 35 - Коэффициенты

Model		Unstandardized Coefficients		Standardized Coefficients	t	Sig.
		B	Std. Error	Beta
1	(Constant)	8,102	,006		1294,350	,000
	F1	9,20E-007	,000	,585	135,718	,000

a  Dependent Variable: LnY

Оценки значимых параметров изменились незначительно, значит, этот признак мультиколлиниарности отсутствует.

- Все оценки параметров имеют логичные знаки и величины с экономической точки зрения, значит, этот признак отсутствует.

- У всех значимых оценок  коэффициентов регрессии имеются небольшие стандартные ошибки и большая значимость, в то время, как всё уравнение в целом значимо (большое значение коэффициента детерминации). Значит, этот признак мультиколлинеарности отсутствует.

Так как все три признака не выполняются, значит, мультиколлинеарность отсутствует.

2)  Регрессионная модель 2.

Таблица 36 – Дисперсионный анализ

Model		Sum of Squares	df	Mean Square	F	Sig.
1	Regression	3479,006	1	3479,006	12936,256	,000(a)
	Residual	10295,029	38281	,269
	Total	13774,035	38282

a  Predictors: (Constant), F2

b  Dependent Variable: LnY

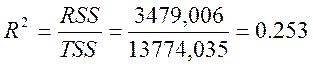
Таблица 37 – Сводка для модели

Model	R	R Square	Adjusted R Square	Std. Error of the Estimate
1	,503(a)	,253	,253	,51859

a  Predictors: (Constant), F2

Значения коэффициента детерминации рассчитанного вручную и взятого из таблицы совпали. Значение коэффициета далеко от 1, значит, уравнение не совсем точно описывает данные.

И так как F_ст.>F_кр., модель в целом является значимой. Значит, эту модель можно использовать для прогнозирования.

Сделана проверка на мультиколлинеарность.

- Изменены исходные данные путем изъятия малого количества (3) наблюдений и оценены неизвестные параметры (табл.35).

Таблица 38 - Коэффициенты

Model		Unstandardized Coefficients		Standardized Coefficients	t	Sig.
		B	Std. Error	Beta
1	(Constant)	8,161	,006		1380,556	,000
	F2	7,51E-008	,000	,582	134,614	,000