Анализ микроданных обследования о расходах на определенную группу услуг (налоги) и уровня благосостояния домохозяйств по выбранному территориальному округу, страница 6

Вывод: с вероятность 12% можно утверждать, что зависимость между налогами и располагаемыми ресурсами является незначимой.

Частный коэффициент корреляции выражает меру линейности зависимости между двумя признаками при исключении влияния остальных признаков.

По полученным значениям можно сказать, что все зависимости обладают очень слабой линейной зависимостью (все частные коэффициенты меньше 0,3).

Для дальнейшего анализа в качестве независимой переменной выбран расход на конечное потребление, который находится в наиболее тесной зависимости с рассматриваемыми расходами населения (налоги, сборы и платежи) (наибольший частный коэффициент корреляции по модулю).

5.  Построены три регрессионные модели:

· 

· 

· 

6.  С помощью МНК найдены оценки неизвестных параметров для каждого уравнения регрессии из п.5 (табл. 29-31).

Для этого созданы две новые переменные F1 = rassq * LN(rassq) и F2 = rassq * (LN(rassq) *  LN(rassq)).

Таблица 29 – Коэффициенты

Model		Unstandardized Coefficients		Standardized Coefficients	t	Sig.
		B	Std. Error	Beta
1	(Constant)	8,196	,006		1267,169	,000
	F1	7,90E-007	,000	,507	114,964	,000

a  Dependent Variable: LnY

Вывод: средний прирост зависимой переменной (ln(у)) при единичном приросте переменной F1 составляет 7,9*10^-7. Среднее значение зависимой переменной ln(y) равно 8,196 при условии, что значение независимой переменной F1 равно нулю.

Таблица 30 – Коэффициенты

Model		Unstandardized Coefficients		Standardized Coefficients	t	Sig.
		B	Std. Error	Beta
1	(Constant)	8,249	,006		1350,030	,000
	F2	6,43E-008	,000	,503	113,738	,000

a  Dependent Variable: LnY

Вывод: средний прирост зависимой переменной (ln(у)) при единичном приросте переменной F2 составляет 6,4*10^-8. Среднее значение зависимой переменной ln(y) равно 8,249 при условии, что значение независимой переменной F2 равно нулю.

Таблица 31 – Коэффициенты

Model		Unstandardized Coefficients		Standardized Coefficients	t	Sig.
		B	Std. Error	Beta
1	(Constant)	7,153	,022		322,772	,000
	F1	1,82E-005	,000	11,659	51,300	,000
	F2	-1,43E-006	,000	-11,154	-49,080	,000

a  Dependent Variable: LnY

Вывод: среднее значение зависимой переменной ln(у) будет равно 7,153, при условии, что оба значения независимых переменных будут равны нулю. Средний прирост ln(y) при единичном приросте F1 составляет 1,82*10^-5, при единичном приросте F2 переменная ln(у) в серднем уменьшается на 1,43*10^-6.

Проверена значимость параметров уравнений из п.5 по критерию Стьюдента.

Значения t_ст. взяты из таблиц 29-31 (t).

t_крит. ≈ 2,021 (a=0,05; N=40).

Т.о. все параметры значимы, т.к. |tст.|>tкрит.

Т.к. все коэффициенты значимы, значит зависимые переменные влияют на ln(y) и константа отлична от нуля.

· 

· 

· 

7.  На основе построенных уравнений зависимости вычислены частные коэффициенты эластичности расходов на налоги от расходов на конечное потребление на всем диапазоне исходных данных.

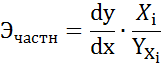
Полученные результаты изображены в таблице 32 (расчеты произведены в SPSS) и на графике на рисунке 17.

Таблица 32 – Коэффициенты эластичности

Э1	Э2	Э3
0,41	0,39	0,79
0,88	0,88	0,71
0,68	0,67	0,87
0,17	0,15	0,38
0,66	0,65	0,88
0,41	0,39	0,79
0,82	0,82	0,77
0,26	0,23	0,56
0,46	0,44	0,83
0,46	0,44	0,83
0,46	0,44	0,83
0,37	0,34	0,73
0,92	0,93	0,65
0,37	0,35	0,74
0,39	0,37	0,77
0,54	0,52	0,88
0,54	0,52	0,88
1,18	1,21	0,27
0,63	0,62	0,89
0,63	0,62	0,89
0,81	0,81	0,78
0,55	0,53	0,88
0,68	0,67	0,87
0,58	0,57	0,89
0,58	0,57	0,89
0,53	0,51	0,88
0,32	0,3	0,67
0,7	0,69	0,86
0,73	0,73	0,84
0,73	0,73	0,84
0,42	0,4	0,8
0,44	0,42	0,82
0,44	0,42	0,82
0,79	0,79	0,8
0,74	0,73	0,84
0,91	0,92	0,66
1,25	1,29	0,15
0,68	0,67	0,87
0,88	0,88	0,7
1,13	1,16	0,34
0,9	0,91	0,67
1,17	1,2	0,27
1,17	1,2	0,27
1,41	1,46	-0,07
0,93	0,93	0,64
1,53	1,6	-0,21