Пространственная структура, образованная атомами, расположенными на одинаковых расстояниях или образующими правильную регулярную последовательность групп (молекул, комплексов), называется к р и с т а л л о м. Частицы как бы закреплены в положениях равновесия, единственной доступной формой движения в отсутствие внешних сил являются беспорядочные по направлению колебания около положений равновесия.
Существует довольно много вариантов пространственного расположения атомов - 230 пространственных групп Федорова-Шенфлиса, которые разделены на 32 кристаллических класса симметрии, иначе их называют точечными группами. Под симметрией понимают способы воспроизводства неограниченного кристалла путем соответствующих манипуляций с выделенным элементом симметрии - ячейкой. Используются:
-трансляция ячейки - последовательный перенос и выстраивание ячейки прикладыванием "кирпичика к кирпичику";
- повороты ячейки вокруг пространственных осей, причем поворот может осуществляться на угол 2 p/n , где n - целое число ( n == 2,3,4,6);
- зеркальное отражение в плоскости;
- центр инверсии и инверсионные оси, если поместить начало координат в центре инверсии, то действие центра инверсии переводит узел с координатами (х,y,z) в узел (-х ,-y ,-z), применение инверсионной оси позволяет кроме такого превращения производить еще и поворот на угол 2 p/n;
- применение винтовой оси n-го порядка, которое совмещает с поворотом трансляцию в направлении вращения.
32 кристаллических класса группируются в семь кристаллических сингоний (син - равный, гонио - угол): триклинная, моноклинная,
ромбическая, тригональная, тетрагональная, гексагональная, кубичес-
кая.
При описании наиболее правильных монокристаллических структур различают 14 трансляционных решеток Бравэ и решетки с базисом.
Р е ш е т к и Б р а в э
С геометрической точки зрения правильное, периодически повторяющееся размещение частиц в кристалле можно описать во многих, но не во всех случаях с помощью операции параллельного переноса - трансляции.
Если выделить в кристаллической решетке элементарную ячейку (рис.1.5.1) как наименьший идентичный элемент, то можно, бесконечно подставляя "кирпичик к кирпичику" соответствующими сторонами, воспроизвести весь макроскопический кристалл вплоть до ступени одноатомной высоты на его поверхностях. Заметим, что "кирпичики" не обязательно должны быть прямоугольными и равносторонними.
Положение любой частицы в
такой идеальной решетке определяется радиус-вектором 
,
находимым из соотношения
(1.5.1)
где m,n,p - целые числа, 
- наименьшие векторы трансляции,
модули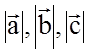 
- периоды трансляции. В вершинах
ячеек располагаются одинаковые атомы или группы атомов, они называются узлами решетки.
Рис.1.5.1. Элементарная ячейка кристаллической решетки
Для описания любой ячейки необходимо задать 6 параметров - 3 ребра (a,b,c) и 3 угла между ними (a,b,g ). Часто за единицу длины при измерениях в решетках берут не линейные системные единицы (м, см, мм, Å ), а отрезки (a,b,c), которые называют в этих случаях осевыми единицами (см. рис.1.5.1), причем нужно иметь в виду, что в низкосимметричных решетках a¹b¹c.
Элементарные ячейки, содержащие атомы лишь в вершинах, называются простыми или примитивными. В некоторых случаях удобнее использовать ячейки, содержащие атомы внутри объема - объемно-центрированные (ОЦ) или в некоторых (или всех) гранях - гранецентрированные (ГЦ) или базоцентрированные (БЦ), но соответствующим подбором атомов в ячейки эти решетки можно свести к примитивным.
Число атомов, принадлежащих одной ячейке, определяется из условия бесконечной протяженности решетки по простым правилам, учитывающим, что каждый из рассматриваемых атомов может принадлежать как одной, так и нескольким смежным ячейкам. На рис.1.5.2 представлены в качестве примера некоторые широко распространенные ячейки с расчетом числа атомов Z, приходящегося на одну ячейку. Всего определено 14 типов трансляционных решеток Бравэ. В табл.1.5.1 они расположены по мере увеличения симметричности (сверху вниз).
 |
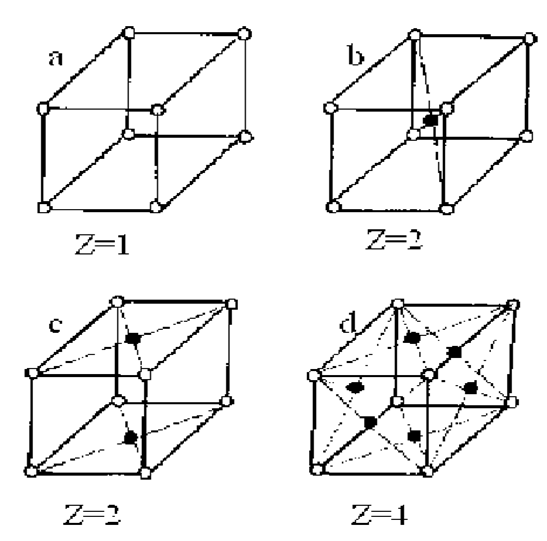Рис.1.5.2. Наиболее распространенные кристаллические решетки металлов и кристаллов: a – простая кубическая, b – объемно-центрированная, с – базоцентрированная, d – гранецентрированная
В пределах классификации решеток Бравэ часто применяется еще и разбиение на группы по веществу, в котором наиболее ясно выражен тип структуры. Среди структур кубической симметрии выделены: В1 типа NaCl (ГЦК), В2 типа CsCl (ОЦК), А1 типа меди, А2 типа вольфрама, А4 типа алмаза, С1 типа CaF2. Строение некоторых наиболее распространенных веществ и типичные структуры будут рассмотрены ниже.
П р и м е ч а н и я:
1. Низшая симметрия - у тригональной сингонии. Она содержит 2 класса: в
первый (1) входят кристаллы, вообще не имеющие симметрии, во второй - имеющие
лишь одну инверсионную ось 1-го порядка, т.е. центр инверсии.
 |
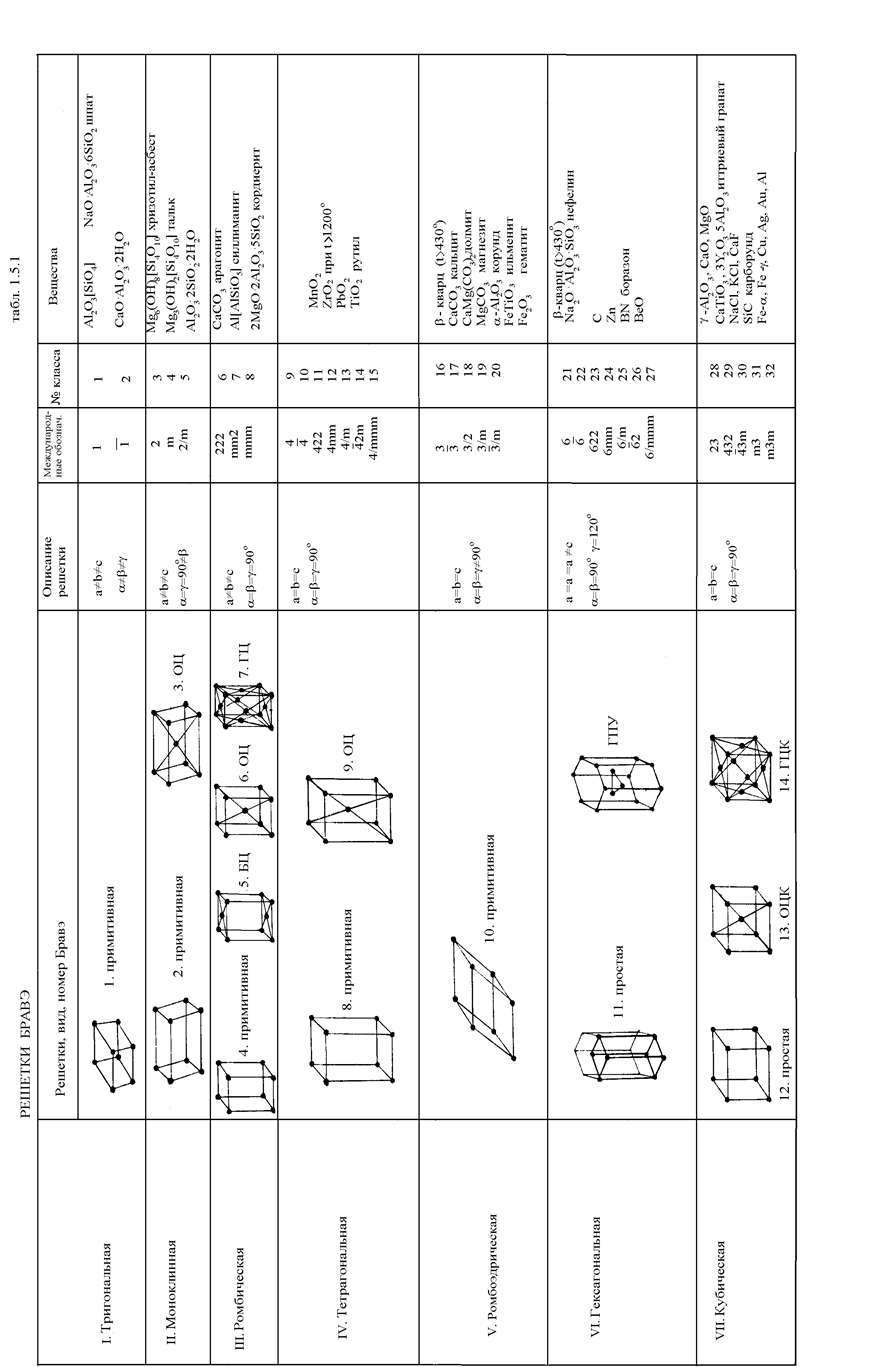У кристаллов моноклинной сингонии имеется одна ось (поворотная или инверсионная) второго порядка. Она обозначена у кристалла 3-го класса цифрой 2, буквой m обозначается наличие плоскости симметрии. У кристаллов 5-го класса имеются ось симметрии 2-го порядка и плоскость симметрии, поэтому он обозначен 2/m.
Соответственно оси симметрии обозначены у кристаллов других сингоний цифрами 3,4,6, наличие нескольких осей одновременно обозначают сочетаниями 222, 422, 622, 432 и т.д. Сочетание mmm обозначает, что у кристалла 8-го класса ромбической сингонии возможны 3 взаимно перпендикулярные плоскости
симметрии, сочетание 4/mmm или 6/mmm обозначает наличие поворотной оси 4 или 6-го порядков (n=4 или n=6), перпендикулярной ей плоскости симметрии и еще 2 плоскостей, перпендикулярных ей.
2. К моноклинной сингонии относятся также такие распространенные виды сырья и продукции, как слюда, гипс, бура. Кристаллы этой сингонии - вообще самые распространенные в природе.
Если кристаллы растут в свободных условиях, например, из солевых растворов или газовой фазы, то они образуют макроскопические кристаллы, внешняя огранка которых соответствует по углам своей сингонии.
Отметим еще, что кроме приведенных в табл. 1.5.1 международных обозначений, в справочной литературе применяются еще и другие обозначения типов решеток, например, В1 типа NaCl обозначается Fm3m или Oh5 , B2 типа CsCl-Pm3m (Oh1), SiO2 ( b - кристобалит) - Fd3m(Oh7) и т.п. Методики определения структуры основаны на рентгеноструктурном анализе, и обозначение всех типов структуры и конкретных структур можно найти в руководствах и справочниках по рентгеноструктурному анализу.
Р е ш е т к и с б а з и с о м
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
