Если направление не проходит через начало координат, то знаки индексов определяются знаками проекций векторов направлений на соответствующие оси. Если проекция вектора направления на данную ось равна 0 (т.е. они взаимно перпендикулярны), то соответствующий индекс равен 0 (рис.1.5.7). Семейство направлений обозначают в угловых скобках <uvw>.
На рис.1.5.7 представлены различные направления и их индексы в кристалле кубической симметрии, там же индексами [100], [010], [001] обозначены положительные направления осей x, y, z. При необходимости в прямоугольной системе координат легко вычислить угол j между двумя направлениями, заданными индексами [u1, v1, w1] и [u2, v2, w2]:
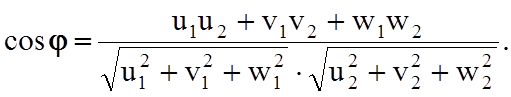
(1.5.2)
И н д е к с ы п л о с к о с т е й, и н д е к с ы М и л л е р а
Положение любой плоскости в пространстве определяется тремя точками. Выберем в качестве таковых точки пересечения плоскости с координатными осями, положение которых совпадает с ребрами элементарной ячейки, а отсекаемые плоскостью отрезки на осях равны (рис.1.5.8): x = ОА = ma, y = OВ = nb , z = ОС = pc, причем m, n, p - целые числа. На рис. 1.4.11, например, 3,2,2; a, b, c - единичные отрезки в осевых единицах.
 |
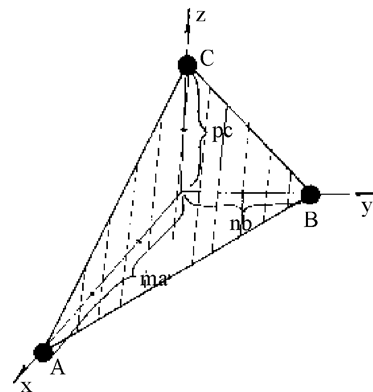Ясно, что во всех случаях все три отрезка ОА, OВ, ОС или отдельные из них описываются дробными цифрами, не имеющими общности даже в пределах решеток одного типа. Поэтому для описания плоскостей в кристаллической решетке применяют наборы чисел, называемые индексами Миллера.
Для получения индексов Миллера для плоскости, изображенной на рис. 1.5.8, возьмем величины, обратные осевым отрезкам:
 |
 |
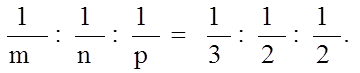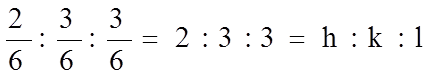Этот набор чисел и есть индексы Миллера (h, k, l), описывающие положение плоскости в пространстве, записываются они в круглых скобках. Если плоскость параллельна какой-либо из осей, то индекс, соответствующий этой оси, будет равен нулю, (ось пересекает эту плоскость в бесконечности, а 1/¥ = 0). Индексы плоскостей могут быть и отрицательными
Для обозначения семейства идентичных плоскостей используются фигурные скобки {hkl}. При этом необходимо помнить, что индексы h, k, l описывают положение в обратном пространстве, т.к. , (рис. 1.5.9).
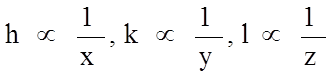
В соответствии с представлениями аналитической геометрии в кристаллографии для определения индексов линии пересечения двух плоскостей (h1k1l1) и (h2k2l2) применяется их векторное произведение:
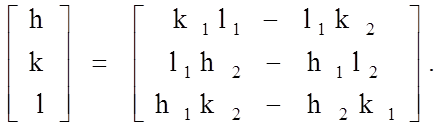(1.5.3)
Таким образом, направление линии пересечения плоскостей
(112) и (111) будет
[110] или Убедиться в этом можно,
сделав соответствующее построение.
 |
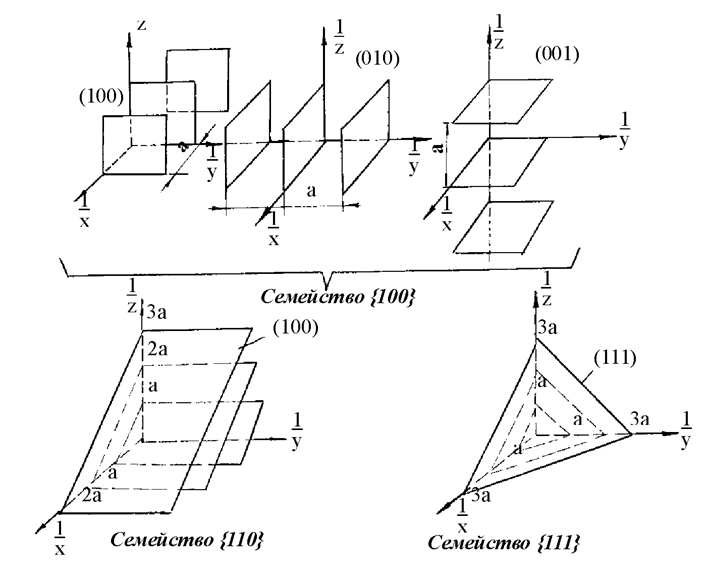Рис.1.5.9. Семейства кристаллографических плоскостей
Символика Миллера из трех индексов обратной решетки применяется для всех кристаллографических систем, кроме гексагональной. Кристаллы гексагональной системы (рис.1.5.10) описывают с помощью четырех осей координат X1, X2, X3 и Z (a1, a2, a3, c), причем оси X1, X2, X3 имеют одинаковый осевой масштаб, лежат в одной плоскости, расходятся через углы шестиугольника, лежащего в основании, под равными углами по 120°. Ось Z перпендикулярна плоскости, где лежат X1, X2, X3. Соответствующий набор 4 чисел называется индексами Миллера-Браве (h, k, i, l), которые образуются так же, как индексы Миллера, т.е. берутся отрезки m, n, p, q, отсекаемые плоскостью на осях, затем вычисляются их обратные величины
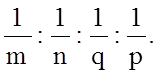h:k:i:l =
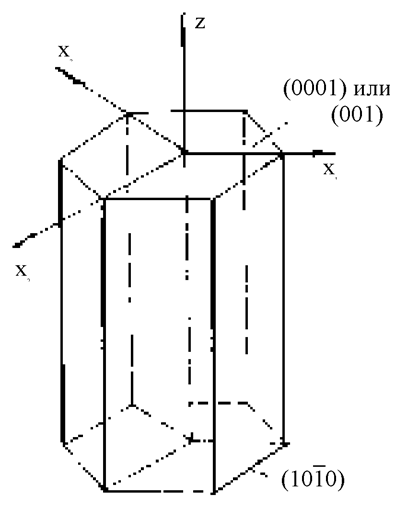
Рис. 1.5.10. Гексагональная решетка с индексами Миллера-Браве
Плоскости, перпендикулярные оси Z [0001], называются базисными. Показано, что индекс i - дополнительный, независимый. Он может быть определен (или исключен) с помощью соотношения (1.5.4):
h + k = -i. (1.5.4)
Соотношение (1.5.4) и сведение четырехкомпонентной системы обозначений к трехкомпонентной (h, k, l) приходится производить всякий раз, когда требуется в кристалле гексагональной симметрии определить индексы направлений. В кристаллографии четырехиндексовое обозначение служит опознавательным знаком гексагональной системы.
О б р а т н а я р е ш е т к а
Индексы Миллера (h, k, l) не задают каждую плоскость однозначно, так как все параллельные плоскости имеют совпадающие индексы, что видно, например, на рис. 1.5.9. При определении индексов Миллера производится сокращение численных значений на общий множитель, в результате поручается набор индексов как наименьших целых чисел, обозначающих набор плоскостей, имеющих общую нормаль. Поскольку
 |
 |
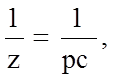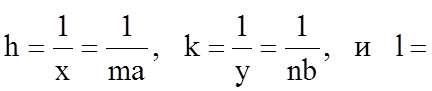то hx + ky + lz = 1. (1.5.5)
Геометрически полученное уравнение можно интерпретировать двояко. Если рассматривать числа h, k, l фиксированными, а x, y, z - переменными, то уравнение определяет набор точек на плоскости. При обратном условии - x, y, z фиксированы, а h, k, l - переменные, уравнение описывает набор плоскостей {hkl}, проходящих через фиксированную точку. О плоскости и соответствующем наборе точек на ней, а также о точке, через которую проходит набор плоскостей, говорят, что они дуальны по отношению друг к другу.
Во многих приложениях
физики твердого тела, в том числе в кристаллографии, набор чисел (hkl) рассматривают как координаты точек другого пространства,
не декартова, с осями x, y, z, а пространства обратной решетки или 
- пространства (пространства Фурье),
пространства волновых векторов. В
пространстве обратной решетки точки 
, обозначающие
плоскости решетки, называются узлами решетки. Они могут быть определены
математическим условием
(целое число). (1.5.6)
Часто условие (5.6) представляют в виде экспоненты
(1.5.7)
Связь точек 
описываемых условием (5.6) с набором
h, k, l
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.