Кристаллические твердые тела, страница 7

Дислокационные линии в объеме прозрачных кристаллов можно наблюдать за счет эффекта декорирования их атомами примесей и вакансиями. Причина та же - наличие областей напряжений сжатия и растяжения вблизи ядра дислокаций. Наконец, в непрозрачных тонкопленочных образцах дислокации могут быть наблюдаемы в электронном микроскопе облучением "на просвет" пучком электронов, ускоренных напряжением 100...200 кВ. В этом случае дислокации обнаруживаются из-за рассеяния электронов на ядрах дислокаций.

Из большого ряда свойств дислокаций применительно к физико-механическим свойствам кристаллов важнейшими являются следующие:

          1. Высокая подвижность дислокаций и их частей - петель, обеспечивающая высокую пластичность кристаллов при малой плотности дислокаций в них.

2. Способность к закреплению за счет накопления около дислокаций точечных дефектов и атомов примесей. Образование этих скоплений, называемых облаками Коттрелла, ведет к упрочнению кристаллов. Непродолжительная (до 1 часа) выдержка кристаллов при повышенной температуре (отпуск) способствует этому процессу.

3. Способность к взаимодействию с препятствиями типа границ зерен, блоков, точечных дисперсных включений, а также друг с другом. Этот процесс ведет к снижению пластичности, увеличению прочности кристаллов, но при достижении некоторого характерного предела возрастающие по мере деформирования поля напряжений приводят к появлению микротрещин (см. ниже).

4. Способность к преодолению далеко отстоящих точечных препятствий типа инородных включений и плоских дефектов типа мало разориентированных блочных и межзеренных границ. На рис. 1.5.17 изображено огибание точечного препятствия, лежащего в плоскости скольжения дислокации, дислокационной линией.

5. Способность к размножению за счет работы внутренних источников под действием внешних механических напряжений. На рис. 1.5.18 изображен принцип действия источника Франка-Рида, представляющего собой часть дислокационной линии, закрепленной на концах взаимодействием с некоторыми дефектами структуры.

 В теории дислокаций рассматриваются также полные и частичные дислокации, геликоидальные, сидячие и другие аналогичные дефекты, заметно влияющие на свойства и поведение кристаллов в тех или иных условиях.

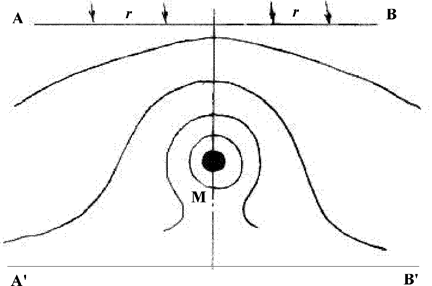Рис. 1.5.17. Огибание дислокационной линией изолированного включения М под действием напряжений сдвига: АВ – начальное положение дислокации, A`B` - ее конечное положение. Около включения остается замкнутая дислокационная петля

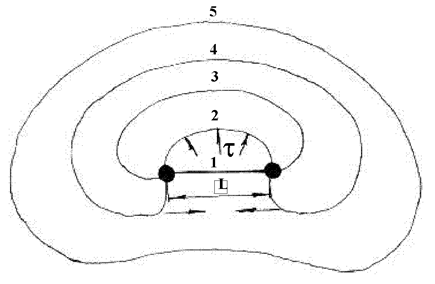Рис. 1.5.18. Принцип действия источника Франка-Рида длиной L под влиянием механических напряжений: 1,2,3,4,5 - стадии формирования свободной дислокационной петли

Н е к о т о р ы е      о с н о в н ы е      а н а л и т и ч е с к и е

с о о т н о ш е н и я   т е о р и и    д и с л о к а ц и й

        Основным количественным параметром, описывающим дислокации, является вектор сдвига или вектор Бюргерса b, по смыслу характеризующий величину элементарного сдвига и по порядку величины близкий к соответствующему параметру решетки (рис.1.5.19).

Рис.1.5.19. К определению вектора Бюргерса b;R- радиус ядра дислокации (R»10Å)

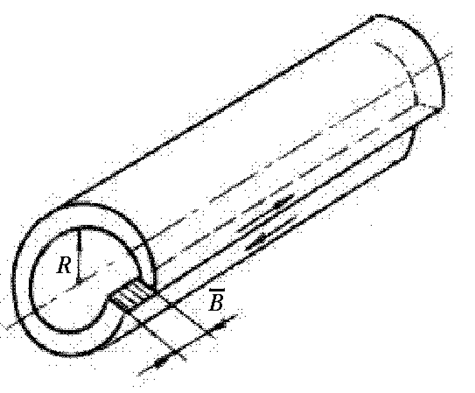При анализе широко используются представления и соотношения классической теории упругости для изотропных и анизотропных тел. Сильно искаженная область ядра дислокации не рассматривается - делают цилиндрический вырез радиусом R. Теоретический анализ  позволяет сделать ряд важных выводов.

1. Каждая дислокация обладает собственным полем напряжений, убывающим от ядра дислокации по закону 1/r. Для винтовой дислокации напряжения равны

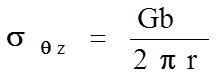                                                                                    (1.5.14)

и однородны по длине и в азимутальном направлении. Используется цилиндрическая система координат, ось z - вдоль оси дислокации, q - азимутальная координата, r - радиальная.

Для краевой дислокации

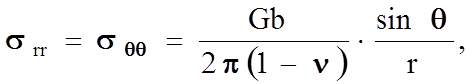                                                                                             (1.5.15)                                                     

где G - модуль сдвига Пуассона,  n - коэффициент Пуассона.

В случае краевой дислокации поле не обладает радиальной симметрией, наблюдается изменение знака напряжений. Оценим величины напряжений в предположении г = 2b, sin q = 1, n = 0,3, т.е. определим максимальные напряжения в объеме, непосредственно примыкающем к ядру дислокаций:

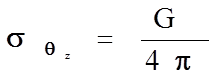 - для винтовой дислокации,

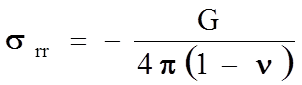      - для краевой дислокации.

В табл.1.5.2 приведены значения G и (s_rr) для некоторых веществ.

Таблица 1.5.2

Максимальные значения модуля сдвига G  и приближенные значения максимальных нормальных напряжений s_rr около дислокаций в некоторых материалах

Вещество	NaCl	MgO	C(алмаз)	a-Fe	Стекло
G,ГПа	16,8	129.6	403,8	109,2	173
»G,кГ/мм2	1680	12960	40380	10920	17300
(srr)max,кГ/мм2	323	1030	6430	1740	2750

Оценка энергии атомов в объеме цилиндра  0< r< R дает величину порядка энергии  плавления, т.е. атомы в ядре дислокации обладают высокой энергией и подвижностью, приближающейся к подвижности в расплавленном состоянии.

2. Энергия деформации, связанная с наличием дислокации в цилиндре единичной высоты (1 см) с радиусом r₁ в теле бесконечной протяженности, составит примерно

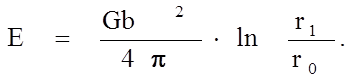(1.5.16)                                                                   

Здесь не учтена небольшая поправка, связанная с влиянием дислокации на изгиб поверхности. Если взять  r₁ = 1 см;  r₀ = 10^-8 см,  ln r/r₀=18,  тогда Е = 1,5Gb²  на единицу длины  L дислокации.

При L»b, примерно равном параметру решетки, т.е. в моноатомном слое, Е = 1,5 b³,  и составит для многих металлов и ионных кристаллов 7,5 эВ.

Вот сюда и уходит энергия, затрачиваемая на формоизменение тела деформацией (прессованием, ковкой, штамповкой, прокаткой, волочением). На создание дислокации длиной 1 см нужно Е»10⁸эВ = 100 МэВ = 1,6×10^-11  Дж, при плотности дислокаций 10¹¹- 10¹² см ^-2 оказывается, что в сильно деформированном кристалле в 1 см³ объема запасено 1,6…16 Дж энергии в виде упругой деформации.