Кристаллические твердые тела, страница 4

индексов Миллера из уравнения (1.5.5) можно установить, если полагать .Тогда    h:k:l = g_x:g_y:g_z. Для вектора обратной решетки  можно записать

                                                                                               (1.5.8)

где h , k , l  - по-прежнему целые числа, а векторы   -  основные

векторы  обратной решетки. Они определяются следующим набором соотношений:

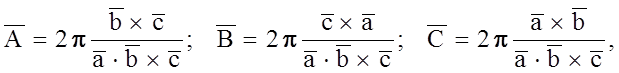                                                                                               (1.5.9)

где   - кристаллографические оси в пространстве x,y,z.

Сомножитель 2p отражает периодичность кристаллической  решетки и функций   описывающих свойства решеток. Если   ортогональны, то, с одной стороны, величина, стоящая в знаменателе соотношения (1.5.9) выражает объем элементарной ячейки, с другой стороны, векторы  также  ортогональны.

Отметим, что в кристаллографии часто сомножитель 2p  в соотношениях (1.5.9) опускают и используют векторы, обозначаемые

Нужно четко представлять, что каждой кристаллографической структуре соответствуют две решетки - реальная кристаллическая и обратная. Они связаны друг с другом соотношением (1.5.9). При повороте кристалла поворачивается и обратная решетка. Например, прямым вычислением можно убедиться, что обратная решетка примитивной кубической решетки есть также кубическая решетка, только при периоде кубической решетки в обычном -пространстве, равном “a”, в обратном пространстве он равен (2p/а). Обратная решетка объемно-центрированной кубической решетки дает гранецентрированную кубическую решетку. Наоборот, обратной, по отношению к гранецентрированной решетке, служит объемно-центрированная. Обратная решетка гексагональной решетки с плотной упаковкой (ГПУ) является также ГПУ-решеткой, но она повернута вокруг оси «с» прямой решетки на 30⁰.

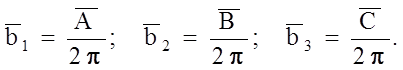Происхождение термина "обратная решетка" связано с единицей измерения единичных векторов. Для векторов  - это метры или Å, а для  - обратные им величины.

Кристаллическая решетка - это решетка в обычном, трехмерном пространстве, а обратная - в другом пространстве, пространстве Фурье, в котором удобно анализировать дифракцию волн, с помощью последней и определяются количественные параметры решеток в рентгенографических, электронографических  и нейтронографических исследованиях.

Представления об обратной решетке были введены в физику Дж. Гиббсом.

1.5.3. Дефекты строения кристаллов

В предыдущих разделах были рассмотрены идеальные или совершенные кристаллы. Предполагалось во всех случаях обязательное существование дальнего порядка в расположении атомов, молекул или атомных групп, образующих структуру теоретически бесконечной протяженности.

Однако, как станет ясно ниже, идеальные по строению кристаллы - не более, чем удобная теоретическая модель, и во многих случаях просто неприменимы в технике. Например, они бы не могли быть деформированы нужным образом, без существования дефектов невозможна термическая обработка металлов и сплавов. Свойства керамических материалов, стекол и пластиков могут быть изменены введением примесей. Электрические свойства полупроводников полностью контролируются введением тарированного количества добавок и изменением совершенства структуры.

Несовершенства структуры играют существенную, а порой определяющую роль в свойствах технических материалов. Тем не менее, при изучении дефектов и несовершенств структуры отправной точкой будет служить идеальный кристалл бесконечной протяженности. Органически присущие любому виду конденсированной материи мгновенные нарушения дальнего порядка, связанные с тепловыми колебаниями, будут рассмотрены отдельно, в разделе, посвященном теплоемкости и другим тепловым свойствам твердых тел.

Остальные дефекты кристаллического тела подразделяются на три обширных класса: точечные, линейные и планарные (поверхностные или плоскостные).                    

1.5.3.1. Точечные дефекты

Любому типу кристаллов органически присущи точечные  дефекты кристаллической решетки. Различают вакансии - узлы кристаллической решетки, покинутые атомами, дислоцированные атомы основного вещества, расположенные в междоузельных пространствах, примесные атомы внедрения, расположенные в междоузельных пространствах решетки, и атомы замещения, вытеснившие атомы основного вещества из узлов решетки. На рис. 1.5.11 представлены основные типы точечных дефектов в кристаллах. В окрестности точечных дефектов наблюдаются локальные искажения электронной конфигурации окружающих атомов.

 В а к а н с и и     и     д и с л о ц и р о в а н н ы е      а т о м ы

Вакансии образуются в объеме как в процессе роста кристаллов из жидкой или газообразной фазы, так и вследствие термофлуктуационных возбуждений, смещающих атомы из их мест в идеальной  решетке. Очень часто эти дефекты возникают при радиационном воздействии на материал.

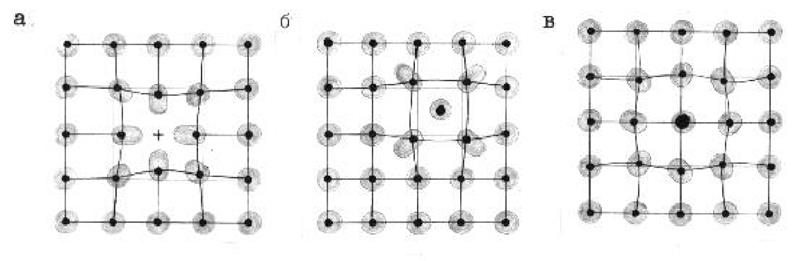Рис. 1.5.11. Точечные дефекты в кристаллической решетке: а - вакансия; б - дислоцированный и примесный атомы внедрения; в - примесный атом замещения

Общепризнанными являются два механизма возникновения точечного дефекта вакансионного типа - механизм Френкеля и механизм Шоттки ("дефекты по Френкелю" и "дефекты по Шоттки").

Энергия смещения атома из занимаемого им места в решетке вообще зависит от того, в какое положение он перемещается - в междоузлие в объеме, или в некоторое  иное положение на свободной поверхности, причем во втором случае всегда требуется меньшая энергия.

На рис.1.5.12 схематически представлены энергии Е₁^* - активации процесса отрыва атома от основных связей для перехода в метастабильное состояние, Е₂^* - активации перехода атома из одного метастабильного состояния в другое незанятое метастабильное состояние (энергия миграции), DЕ - энергия образования дефекта.

Когда такое "испарение" атомов происходит внутри объема, то реализуется механизм возникновения "дефектов по Френкелю", в виде пары "вакансия - дислоцированный атом" (рис.1.5.13,а). Несколько иначе реализуется механизм возникновения вакансии по Шоттки  (рис.1.5.13,6). В этом случае происходит полное или частичное испарение атомов с поверхности кристаллов. В первом случае атом переходит в положение над поверхностью, сохраняя некоторые  связи с атомами объема, при полном испарении атомы покидают объем твердого тела, выходя в фазу пара. В том и другом случае в поверхностном слое остается вакансия, со временем заполняемая атомом объема, дислоцированные атомы не возникают.